北师大版数学八年级上册单元分层检测卷第三章《位置与坐标》B卷

试卷更新日期：2025-09-12 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 在平面直角坐标系中，将点P（﹣3，2）向右平移3个单位长度到P₁处，则点P₁的坐标为（　　）

A、（﹣6，2） B、（0，2） C、（﹣3，5） D、（﹣3，﹣1）

查看试题解析
2. 剪纸是我国民间艺术之一，如图放置的剪纸作品，它的对称轴与平面直角坐标系的坐标轴重合.则点 $A (- 4, 2)$ 关于对称轴对称的点的坐标为（）

A、 $(- 4, - 2)$ B、 $(4, - 2)$ C、 $(4, 2)$ D、 $(- 2, - 4)$

查看试题解析
3. 如图，甲处表示2街6巷的十字路口，乙处表示6街1巷的十字路口．如果用（2，6）表示甲处的位置，那么“（2，6）→（3，6）→（4，6）→（5，6）→（6，6）→（6，5）→（6，4）→（6，3）→（6，2）→（6，1）”表示从甲处到乙处的一种路线（规定：只能沿线向下和向右运动），则从甲处到乙处的路线中经过丙处的走法共有（　　）

A、38种 B、39种 C、40种 D、41种

查看试题解析
4. 如图，已知点 $A (1 ， 0)$ ， $B (4 ， m)$ ，若将线段 $A B$ 平移至 $C D$ ，其中点 $C (- 2 ， 1)$ ， $D (a ， n)$ ，则 $m - n$ 的值为（）

A、 $- 3$ B、 $- 1$ C、 $1$ D、 $3$

查看试题解析
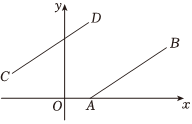5. 对于正整数x，规定函数 $f (x) = {\begin{array}{l} 3 x + 1 (x 为奇数) \\ \frac{1}{2} x (x 为偶数) \end{array}$ ．在平面直角坐标系中，将点 $(m, n)$ 中的 $m$ ， $n$ 分别按照上述规定，同步进行运算得到新的点的横、纵坐标（其中 $m$ ， $n$ 均为正整数）．例如，点 $(8, 5)$ 经过第 $1$ 次运算得到点 $(4, 16)$ ．经过第 $2$ 次运算得到点 $(2, 8)$ ，经过第 $3$ 次运算得到点 $(1, 4)$ ，经过有限次运算后，必进入循环圈，按上述规定，将点 $(2, 1)$ 经过第 $2025$ 次运算后得到点是（）

A、 $(2, 1)$ B、 $(4, 2)$ C、 $(1, 2)$ D、 $(1, 4)$

查看试题解析
6. 某广场计划用如图①所示的A ， B两种瓷砖铺成如图②所示的图案．第一行第一列瓷砖的位置记为（1，1），其右边瓷砖的位置记为（2，1），其上面瓷砖的位置记为（1，2），按照这样的规律，下列说法正确的是（　　）

A、（2024，2025）位置是B种瓷砖 B、（2025，2025）位置是B种瓷砖 C、（2026，2026）位置是A种瓷砖 D、（2025，2026）位置是B种瓷砖

查看试题解析
7. 已知在第二象限内的点 $P$ 的坐标为 $(2 a - 3, 6 + a)$ ，且点 $P$ 到两坐标轴的距离相等，则点 $P$ 的坐标是（）

A、 $(- 5, 5)$ B、 $(5, - 5)$ C、 $(- 5, 5)$ 或 $(- 15, 15)$ D、 $(5, - 5)$ 或 $(15, - 15)$

查看试题解析
8. 如图，在平面直角坐标系中有A（-1，1），B（-1，-2），C（3，-2），D（3，1）四点，一只瓢虫从点A 出发以2个单位长度/秒的速度沿A→B→C→D→A 循环爬行，则第 2021 秒瓢虫在（）

A、（3，1）处 B、（-1，-2）处 C、（1，-2）处 D、（3，-2）处

查看试题解析
9. 如图，在平面直角坐标系中，A₁（1，2），A₂（2，0），A₃（3， ﹣2），A₄（4，0）…根据这个规律，探究可得点 A₂₀₂₂ 的坐标是（）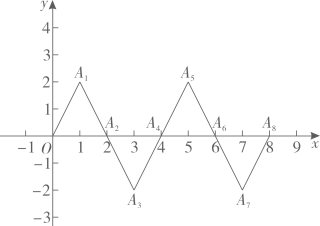

A、（2022，0） B、（2022，2） C、（2021，﹣2） D、（2022，﹣2）

查看试题解析
10. 如图，一个粒子在第一象限内及x轴、y轴上运动，第一分钟，它从原点运动到点(1，0)，第二分钟，它从点(1，0)运动到点(1，1)，而后接着按图中箭头所示在与x轴、y轴平行的方向上来回运动，且每分钟移动1个单位长度，那么在第2 022分钟时，这个粒子所在位置的坐标是( )

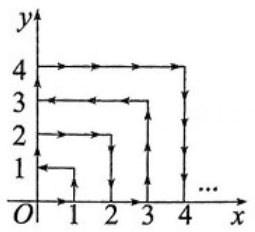A、(44，4) B、(44，3) C、(44，2) D、(44，1)

查看试题解析

二、填空题（每题3分，共18分）

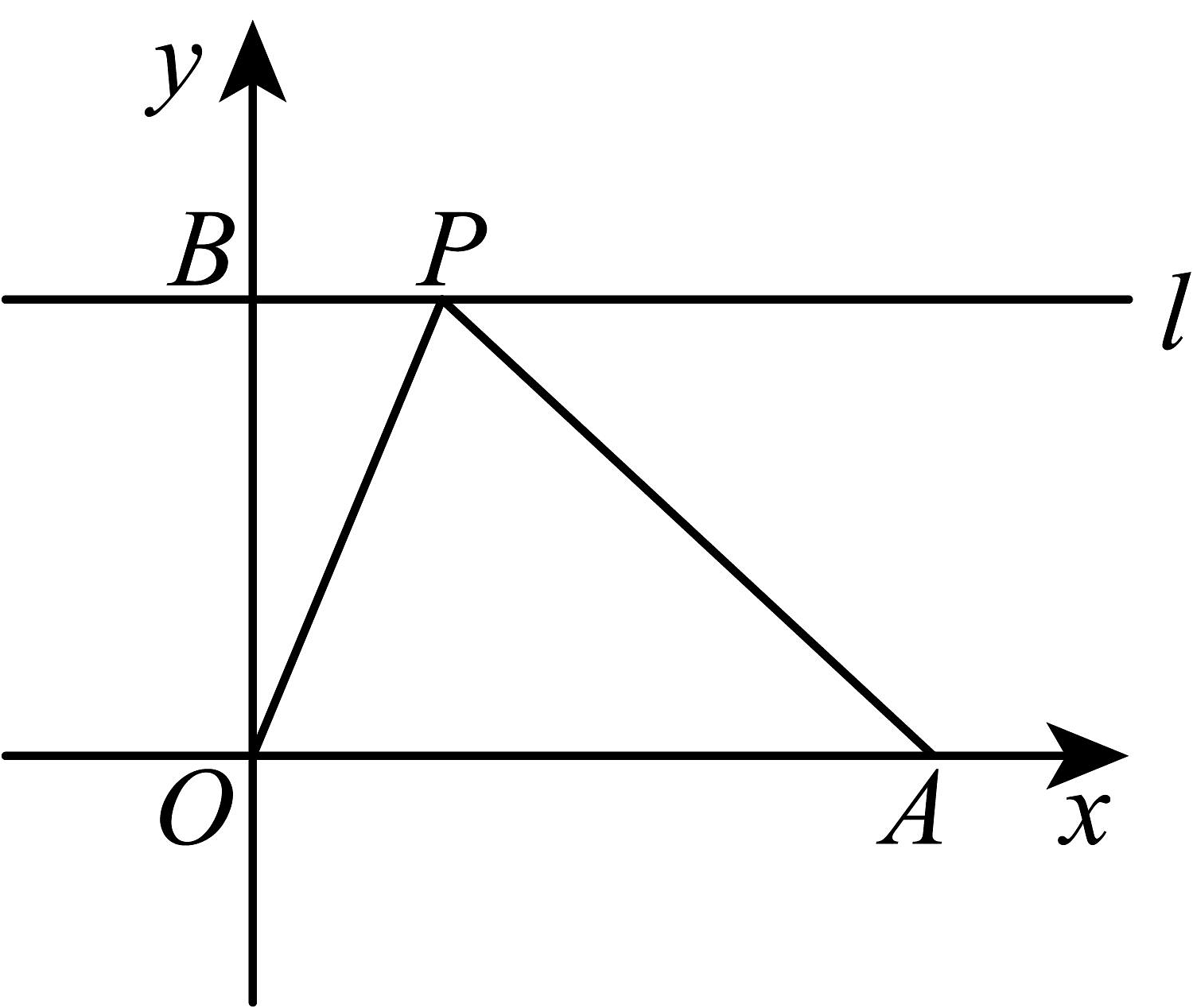
11. 如图，在平面直角坐标系 $x O y$ 中，已知 $A (5, 0)$ ， $B (0, 4)$ ，过点B作y轴的垂线l，P为直线l上一动点，连接 $P O$ ， $P A$ ，则 $P O + P A$ 的最小值为．

查看试题解析
12. 如图，已知点A， B的坐标分别为 $(2, 4)$ ， $(6, 0)$ ，将 $△ O A B$ 沿x轴向右平移，使点B平移到点E，得到 $△ D C E$ ，若 $O E = 8$ ，则点C的坐标为．

查看试题解析
13. 如图，弹性小球从点P（0，3）出发，沿所示方向运动，每当小球碰到矩形OABC的边时反弹，反弹时反射角等于入射角，当小球第1次碰到矩形的边时的点为P₁ ，第2次碰到矩形的边时的点为P₂ ， …，第n次碰到矩形的边时的点为P_n ，则点P₃的坐标是；点P₂₀₁₄的坐标是.

查看试题解析
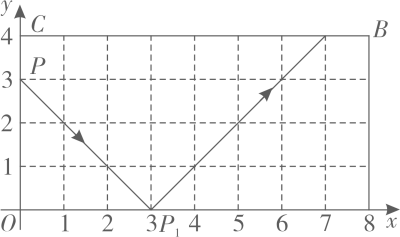14. 在平面直角坐标系中，已知点A的坐标为(a，b)，且a，b满足 $(a - 2)^{2} + | b + 3 | = 0$ ，则点A在第象限.

查看试题解析
15. 象棋在中国有着悠久的历史，在春秋战国时代的文化名著《楚辞·招魂》中就有“蔽象棋，有六博兮”的词句，说明在当时已经有了“象棋”这个名词．如图，这是象棋的对弈图（部分），若棋子“帅”表示点 $(0, - 3)$ ，棋子“仕”表示点 $(- 1, - 3)$ ，则棋子“马”所在点的坐标是．

查看试题解析
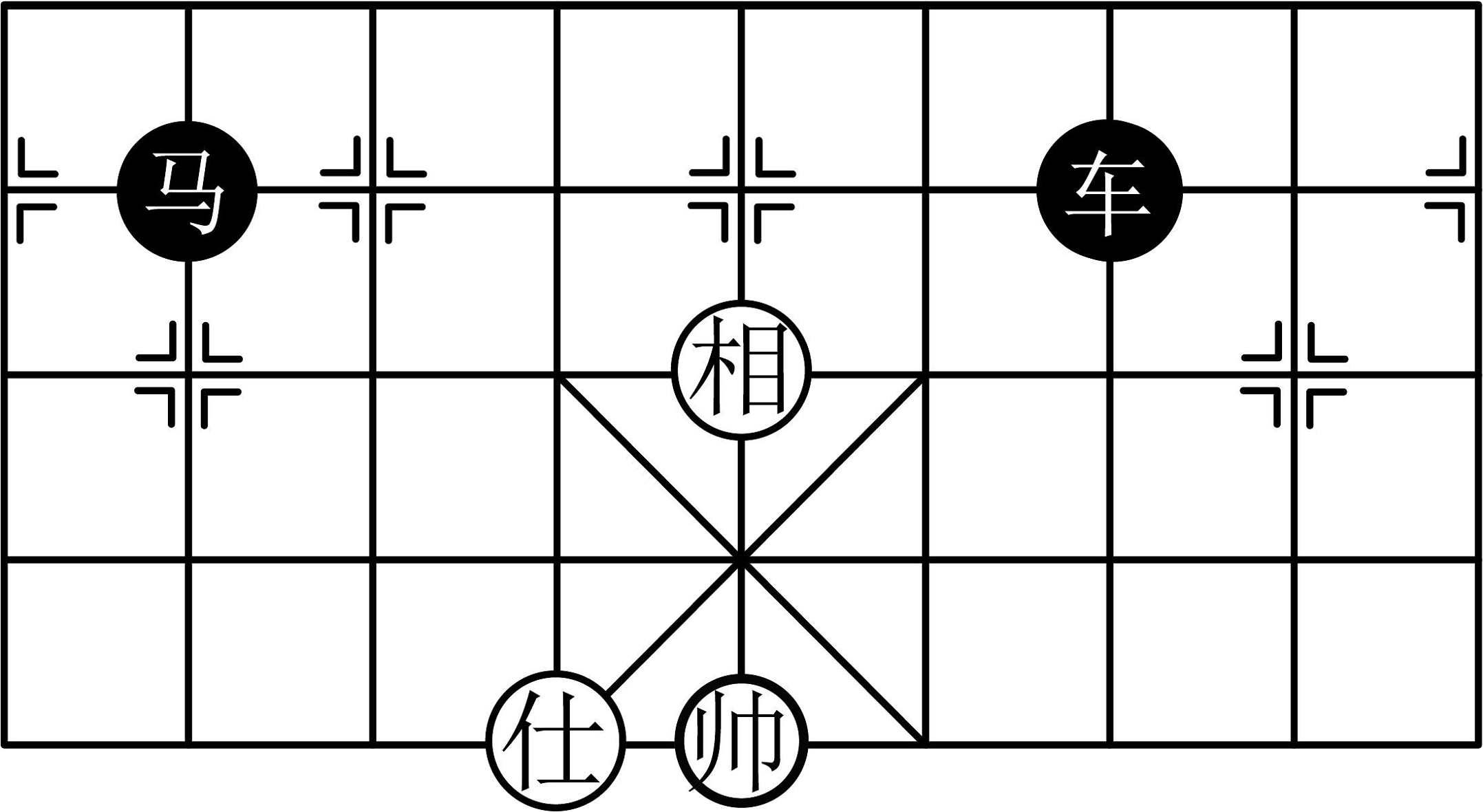16. 在平面直角坐标系中，对 $△ A B C$ 进行循环往复的轴对称变换，若原来点 $A$ 的坐标是 $(\sqrt{3} ， \sqrt{2})$ ，则经过第2021次变换后所得的点 $A$ 的坐标是．

查看试题解析

三、解答题（共8题，共72分）

17. 如图，在平面直角坐标系中，过点 $A (0 ， 4)$ 的直线 $a ⊥ y$ 轴， $M (9 ， 4)$ 为直线a上一点．点P从点M出发，以每秒2个单位长度的速度沿直线a向左移动；同时，点Q从原点出发，以每秒1个单位长度的速度沿x轴向右移动．

(1)、当点P在线段 $A M$ 上移动时，几秒后 $A P = O Q$ ？

(2)、若以A，O，Q，P为顶点的四边形的面积是10，求点P的坐标．

查看试题解析
18. 我省某大学生机器人战队在全国比赛中取得优异成绩，机器人的行走由编程控制，可近似理解为机器人站在格点上，把行走区域看作网格，沿格线行走，每走一步为一个单位长度，然后转化为程序语言．如图，从点B走到点C记作 $(1, 2)$ ，从点B走到点A记作 $(- 2, - 1)$ ．

(1)、从点B到点D可记作______．

(2)、若一个机器人从点C出发，按照 $(- 2, - 2), (- 2, 1), (2, - 3), (- 1, 2)$ 行走后到达点E，请在图中标出点E的位置．

(3)、若图中另有两个格点M，N，从点M走到点A记作 $(m + 1, n - 4)$ ，从点M走到点N记作 $(m + 5, n - 2)$ ，则点A走到点N应记作什么？

查看试题解析
19. 在平面直角坐标系中，已知点 $M (m ， 2 m + 3)$ ．

(1)、若点 $M$ 在 $x$ 轴上，求 $m$ 的值；

(2)、若点 $M$ 在第一、三象限的角平分线上，求 $m$ 的值．

(3)、若点 $N$ 坐标 $(- 2 ， 5)$ ，并且 $M N ∥ y$ 轴，求 $M$ 点坐标．

查看试题解析
20. 在平面直角坐标系xOy中，对于点 $P (x, y)$ ，若点Q的坐标为 $(a x + y, x + a y)$ ，则称点Q是点P的“a阶派生点”（其中a为常数，且 $a \neq 0$ ）．例如：点 $P (1, 4)$ 的“2阶派生点”为点 $Q (2 \times 1 + 4, 1 + 2 \times 4)$ ，即点 $Q (6, 9)$ ．

(1)、若点P的坐标为 $(- 1, 5)$ ，则它的“3阶派生点”的坐标为；

(2)、若点P的“5阶派生点”的坐标为 $(- 9, 3)$ ，求点P的坐标；

(3)、若点 $P (c + 1, 2 c - 1)$ 先向左平移2个单位长度，再向上平移1个单位长度后得到了点 $P_{1}$ ．点 $P_{1}$ 的“ $- 4$ 阶派生点” $P_{2}$ 位于坐标轴上，求点 $P_{2}$ 的坐标．

查看试题解析
21. 在平面直角坐标系中，直线l过点M(3，0)，且平行于y轴.

(1)、已知△ABC三个顶点的坐标分别是A(-2，0)，B(-1，0)，C(-1，2)，△ABC关于y轴的对称图形是△A₁B₁C₁ ， △A₁B₁C₁关于直线l的对称图形是△A₂B₂C₂ ，写出△A₂B₂C₂三个顶点的坐标.

(2)、已知点P(-a，0)，其中a>0，点P关于y轴的对称点是P₁ ，点P₁关于直线l的对称点是P₂ ，求PP₂的长.

查看试题解析
22. 在平面直角坐标系中， $O$ 为坐标原点，过点 $A (8, 6)$ 分别作 $x$ 轴、 $y$ 轴的平行线，交 $y$ 轴于点 $B$ ，交 $x$ 轴于点 $C$ ，点 $P$ 是从点 $B$ 出发，沿 $B \to A \to C$ 以 $2$ 个单位长度 $/$ 秒的速度向终点 $C$ 运动的一个动点，运动时间为 $t$ （秒）．

(1)、直接写出点 $B$ 和点 $C$ 的坐标．

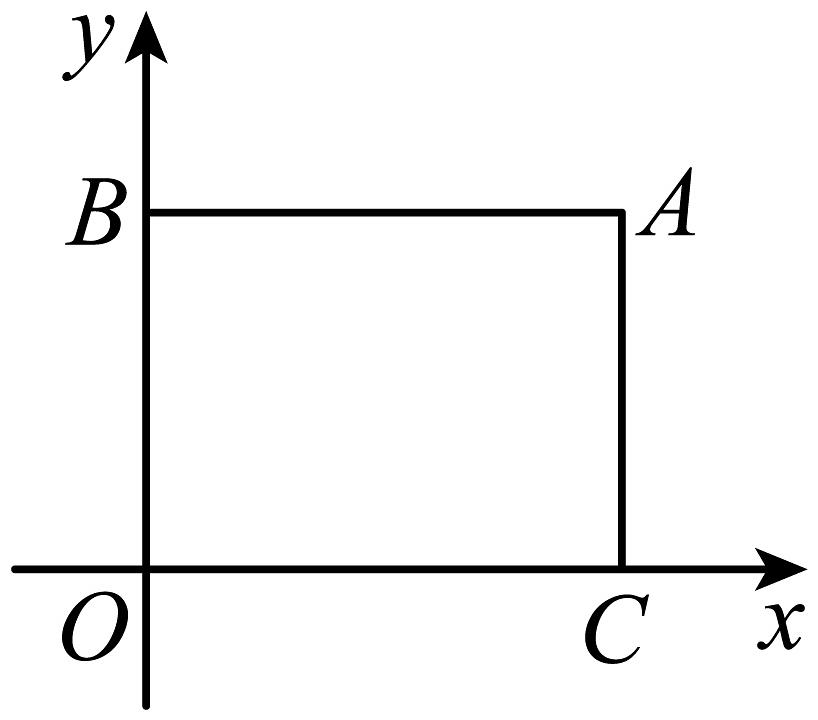(2)、点 $P$ 在运动过程中，是否存在这样的 $t$ 值，使三角形 $A P O$ 的面积等于四边形 $A B O C$ 面积的四分之一，若存在，请求出 $t$ 值，若不存在，请说明理由．

查看试题解析
23. $△ A B C$ 与 $△ A^{'} B^{'} C^{'}$ 在平面直角坐标系中的位置如图所示．

(1)、分别写出下列各点的坐标：A；B；C；

(2)、 $△ A B C$ 由 $△ A^{'} B^{'} C^{'}$ 经过怎样的平移得到？答：．

(3)、若点 $P (x ， y)$ 是 $△ A B C$ 内部一点，则 $△ A^{'} B^{'} C^{'}$ 内部的对应点 $P^{'}$ 的坐标为；

(4)、求 $△ A B C$ 的面积，

查看试题解析
24. 如图，在平面直角坐标系中，已知 $A (a ， 0)$ ， $B (b, 0)$ ，其中a，b满足 $\sqrt{a + 1} + {(b - 3)}^{2} = 0$ ．

(1)、填空： $a =$ ， $b =$ ；

(2)、若在第三象限内有一点 $M (- 2, m)$ ，用含m的式子表示 $△ A B M$ 的面积；

(3)、在（2）条件下，线段 $B M$ 与y轴相交于 $C (0, - \frac{9}{10})$ ，当 $m = - \frac{3}{2}$ 时，点P是y轴上的动点，当满足 $△ P B M$ 的面积是 $△ A B M$ 的面积的2倍时，求点P的坐标．

查看试题解析

北师大版数学八年级上册单元分层检测卷第三章 《位置与坐标》B卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共8题，共72分）

北师大版数学八年级上册单元分层检测卷第三章《位置与坐标》B卷