浙教版数学八年级上学期重难点复习4：等腰三角形的分类讨论

试卷更新日期：2025-09-12 类型：复习试卷

进入出卷网下载

一、对边或角的讨论

1. 已知等腰三角形两边的长分别为3和7，则此等腰三角形的周长为（）

A、13 B、17 C、13或17 D、13或10

查看试题解析
2. 在等腰三角形ABC中，若∠A＝70°，则∠B的度数是（　　）

A、40° B、55° C、70° D、40°或55°或70°

查看试题解析
3. 已知一等腰三角形的一个内角为80°，则这个等腰三角形顶角的度数为

查看试题解析
4. 若一个等腰三角形的三边长分别为x，2x，5x-3，则这个等腰三角形的周长为.

查看试题解析
5. 概念学习
规定：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”．
从三角形 $($ 不是等腰三角形 $)$ 一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”．

(1)、理解概念：判断下列说法是否正确（对的打√，错的打×）
①全等三角形是“等角三角形”（）
②如图 $1$ ，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $C D ⊥ A B$ ，图中共有2对“等角三角形”（）
③如图 $1$ ，在 $Rt △ A B C$ 中， $A C \neq B C ， ∠ A C B = 90 °$ ， $C D ⊥ A B$ ，无论 $∠ A$ 为何值， $C D$ 都不可能是 $△ A B C$ 的“等角分割线”（）

(2)、概念应用：如图 $2$ ，在 $△ A B C$ 中， $C D$ 为角平分线， $∠ A = 40 °$ ， $∠ B = 60 ° .$ 求证： $C D$ 为 $△ A B C$ 的等角分割线．

(3)、在 $△ A B C$ 中， $∠ A = 24 °$ ， $C D$ 是 $△ A B C$ 的等角分割线，直接写出 $∠ A C B$ 的度数．

查看试题解析
6. 数学课上，张老师举了下面的例题：
例1 在等腰三角形ABC 中，∠A=110°，求∠B 的度数.(答案：35°)
例2 在等腰三角形ABC 中，∠A=40°，求∠B 的度数.(答案：40°或70°或100°)
张老师启发同学们进行变式，小敏编了如下一题：
变式在等腰三角形ABC 中，∠A=80°，求∠B 的度数.

(1)、请你解答以上的变式题.

(2)、解(1)后，小敏发现，∠A 的度数不同，得到∠B 的度数的个数也可能不同.如果在等腰三角形ABC中，设 $∠ A = x^{\circ} ，$ ，当∠B 有三个不同的度数时，请你探索x 的取值范围.

查看试题解析

二、遇中线，高或垂直平分线的讨论

7. 等腰三角形一腰上的中线把这个三角形的周长分成 $1 : 2$ 两部分，已知这个等腰三角形的周长为 $72 cm$ ，则这个等腰三角形的底边为（） $cm$ ．

A、8 B、20 C、40 D、8或40

查看试题解析
8. 定义：如果经过三角形一个顶点的线段把这个三角形分成两个小三角形，其中一个三角形是等腰三角形，另外一个三角形和原三角形的三个内角分别相等，那么这条线段称为原三角形的“和谐分割线”，例如：如图1，等腰直角三角形斜边上的中线就是一条“和谐分割线”．

(1)、判断命题真假：等边三角形存在“和谐分割线”是______命题；（填“真”或“假”）

(2)、如图2，在Rt△ABC中， $∠ C = 90 ° ， ∠ B = 30 ° ， A C = \sqrt{3}$ ，试探索Rt△ABC是否存在“和谐分割线”？若存在，求出“和谐分割线”的长度；若不存在，请说明理由；

(3)、如图3，在 $△ A B C$ 中， $A = 42 °$ ，若线段 $C D$ 是 $△ A B C$ 的“和谐分割线”，且 $△ B C D$ 是等腰三角形，求出所有符合条件的 $∠ B$ 的度数．

查看试题解析

三、遇动点和动线段需要讨论

9. 在 $△ A B C$ 中， $C A = C B = 2, ∠ A C B = 12 0^{°}$ ，将一块足够大的直角三角尺 $P M N (∠ M = 9 0^{°}, ∠ M P N = 3 0^{°})$ 按如图所示放置，顶点 $P$ 在线段AB上滑动，PM始终经过点 $C$ ，斜边PN交AC于点 $D$ .在点 $P$ 滑动过程中， $△ P C D$ 为等腰三角形时，则点 $P$ 与点 $B$ 的距离BP为.

查看试题解析
10. 如图，四边形ABCD是长方形，AB=x，BC=4，点P为直线AD上的一点．若满足△BCP为等腰三角形的点P有且仅有3个，则x=.

查看试题解析
11. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 8$ ， $A B = 10$ ，动点 $D$ 从点 $A$ 出发，沿线段 $A B$ 以每秒 $2$ 个单位的速度向 $B$ 运动，过点 $D$ 作 $D F ⊥ A B$ 交 $B C$ 所在的直线于点 $F$ ，连结 $A F$ ， $C D .$ 设点 $D$ 运动时间为 $t$ 秒．当 $△ A B F$ 是等腰三角形时，则 $t =$ 秒．

查看试题解析
12. 如图，长方形ABCD中，AB＝4cm，BC＝6cm，现有一动点P从A出发以2cm/秒的速度，沿矩形的边A—B—C—D—A返回到点A停止，点P的运动时间为t秒．
（1）当t＝3秒时，BP＝ cm；
（2）当t为何值时，连结CP，DP，△CDP为等腰三角形；
（3）Q为AD边上的点，且DQ＝5，当t为何值时，以长方形的两个顶点及点P为顶点的三角形与△DCQ全等．

查看试题解析

四、构造等腰三角形需要讨论

13. 已知在等腰三角形ABC中，AB=AC，∠CAB=108°，D是直线BC上一点(不与点B，C重合)，连结AD，若△ABD是等腰三角形，则∠DAC= ．

查看试题解析
14. 如图所示的直角三角形ABD是某等腰三角形对称轴的一侧，请补全该等腰三角形.(只需画出图形)

查看试题解析
15. 如图是由25个边长为1的小正方形组成的5×5网格，请分别在3个网格图中画出3个互不全等的等腰三角形，要求：等腰三角形顶点在格点上，且腰长为5．

查看试题解析
16. 如果一个三角形被一条线段分割成两个等腰三角形，那么这种分割叫做等腰分割，这条线段称为这个三角形的等腰分割线．如图1，当 $△ A B D$ 和 $△ A C D$ 为等腰三角形时， $A D$ 为 $△ A B C$ 的等腰分割线．

(1)、如图2， $△ A B C$ 中， $∠ B = 2 ∠ C$ ，线段 $A C$ 的垂直平分线 $E D$ 交 $A C$ 于点 $D$ ，交 $B C$ 于点 $E$ ．求证： $A E$ 是 $△ A B C$ 的一条等腰分割线．

(2)、如图3，在 $△ A B C$ 中， $∠ A = 120 °$ ， $∠ B = 20 °$ ， $∠ C = 40 °$ ，请你用两种不同的方法完成 $△ A B C$ 的等腰分割，并直接写出每种分割之后两个等腰三角形的顶角度数．

(3)、在 $△ A B C$ 中， $A D$ 为 $△ A B C$ 的等腰分割线，且 $A D = B D$ ， $∠ C = 30 °$ ，请直接写出 $∠ B$ 的度数．

查看试题解析
17. $△ A B C$ 为等边三角形，射线 $A P$ 经过点A， $∠ B A P = α (0 ° < α < 90 °)$ ，画点B关于射线 $A P$ 的对称点D，连接 $A D$ 、 $C D$ 交直线 $A P$ 于点E．

(1)、如图，当 $0 ° < α < 60 °$ 时
①依题意补全图形；
②用等式表示线段 $E A$ 、 $E D$ 、 $E C$ 的数量关系，并证明；

(2)、若 $△ D B C$ 为等腰三角形，直接写出 $α$ 的度数．

查看试题解析
18. 如图，已知 $△ A B C$ 是等边三角形， $B C = 2 c m$ ，点P从点A出发，沿射线 $A B$ 以 $1 c m / s$ 的速度运动，过点P作 $P E ∥ B C$ 交射线 $A C$ 于点E，同时点Q从点C出发沿 $B C$ 的延长线以 $1 c m / s$ 的速度运动，连接 $B E$ 、 $E Q$ ，设点P的运动时间为 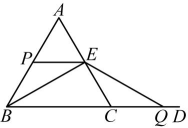$t (s)$ ．

(1)、当点P在边 $A B$ 上，且不与点 $A$ 、 $B$ 重合时，求证： $△ B P E ≌ △ E C Q$ ；

(2)、直接写出 $C E$ 的长（用含t的代数式表示）；

(3)、在不添加字母和连接其它线段的条件下，当图中等腰三角形的个数大于3时，直接写出t的值和对应的等腰三角形的个数．（请写出所有的可能性）

查看试题解析