第三章《图形的初步认识》提升卷—华东师大版数学七（上）单元测

试卷更新日期：2025-09-13 类型：单元试卷

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分

1. 下列各组图形都是平面图形的是( )

A、三角形、圆、球、圆锥 B、点、线段、棱锥、棱柱 C、角、三角形、正方形、圆 D、点、角、线段、长方体

查看试题解析
2. 下列三个生活，生产现象：
①用两个钉子就可以把木条固定在墙上；
②植树时，只要定出两棵树的位置，就能确定同一行树所在的直线；
③把弯曲的公路改直，就能缩短路程．
其中可用基本事实＂两点确定一条直线＂来解释的现象有

A、①③
B、①②
C、②③
D、③

查看试题解析
3. 如图，正方体的6个面上分别标有字母A，B，C，D，E，F，将该正方体按图示方式转动，根据图形可得，与字母F相对的是（）

A、字母A B、字母B C、字母C D、字母E

查看试题解析
4. 如图是由大小相同的小正方体拼成的几何体，若移走一块小正方体后，几何体从左面看的形状图发生改变，则移走的小正方体是（）

A、① B、② C、③ D、④

查看试题解析
5. 如图是由几个小立方块所搭成的几何体的俯视图，小正方形中的数字表示在该位置上小立方块的个数，则这个几何体的左视图为（）

A、 B、 C、 D、

查看试题解析
6. 如图是正方体的表面展开图，若正方体中相对的面上的数互为相反数，则 $x$ 的值为（）

A、 $- 5$ B、 $- 3$ C、 $- 2$ D、2

查看试题解析
7. 如图，点M在线段AN的延长线上，且线段MN=20，第一次操作：分别取线段AM和AN的中点 $M_{1} ， N_{1}$ ；第二次操作：分别取线段 $A M_{1}$ 和 $A N_{1}$ 的中点 $M_{2}, N_{2}$ ；第三次操作：分别取线段 $A M_{2}$ 和 $A N_{2}$ 的中点 $M_{3}, N_{3}$ ；……连续这样操作10次，则每次的两个中点所形成的所有线段之和 $M_{1} N_{1} + M_{2} N_{2} + \dots + M_{10} N_{10} =$ ( )

A、 $20 - \frac{10}{2^{9}}$ B、 $20 + \frac{10}{2^{9}}$ C、 $20 - \frac{10}{2^{10}}$ D、 $20 + \frac{10}{2^{10}}$

查看试题解析
8. 如图，从早上 $7 : 20$ 到同一天早上 $9 : 00$ ，时钟的分针旋转了（）

A、 $180 °$ B、 $420 °$ C、 $540 °$ D、 $600 °$

查看试题解析
9. 将一副直角三角板按如图所示各位置摆放，其中∠a与∠β一定互余的是（）

A、 B、 C、 D、

查看试题解析
10. 如图，点 $O$ 为线段 $A D$ 外一点， $M$ ， $C$ ， $B$ ， $N$ 为 $A D$ 上顺次排列的四点，连接 $O M$ ， $O C$ ， $O B$ ， $O N$ ，在下列结论中：

①以 $O$ 为顶点的角有15个；
②若 $O M$ 平分 $∠ A O C$ ， $O N$ 平分 $∠ B O D$ ， $∠ A O D = 4 ∠ C O B$ ，则 $∠ M O N = \frac{3}{2} (∠ M O C + ∠ B O N)$
③若 $M$ 为 $A B$ 的中点， $N$ 为 $C D$ 的中点，则 $M N = \frac{1}{2} (A D - C B)$ ；
④若 $M C = C B$ ， $M N = N D$ ，则 $C D = 2 C N$ ．
其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题：本大题共5小题，每小题3分，共15分

11. 一个棱柱有12个顶点，所有侧棱长的和是48cm，则每条侧棱长是。

查看试题解析
12. 如图，这是由若干个大小相同的小正方体组合而成的几何体，那么从三个方向看到的平面图形中，面积最大的是从面看．（填“上”“正”或“左”）

查看试题解析
13. 图所示是一个正方体的表面展开图，且相对两个面表示的整式的和都相等．如果 $A = a^{3} + \frac{1}{5} a^{2} b + 3, B = \frac{1}{2} a^{2} b - 3, C = a^{3} - 1, D = - \frac{1}{2} (a^{2} b - 6)$ ，那么F所代表的整式是．

查看试题解析
14. 复原绳子如图所示，把一根绳子对折成一条线段AB，P是AB 上一点，且 $A P = \frac{1}{2} P B,$ 若在点 P 处将绳子剪断，且剪断后的各段绳子中最长的一段为40cm.则绳子的原长为cm.

查看试题解析
15. 用边长为 $1$ 的正方形纸板，制成一个七巧板（如图①），将它拼成“小天鹅”图案（如图②），其中阴影部分的面积为.

查看试题解析

三、解答题：本大题共9小题，共75分

16. 如图，平面内四点 $A, B, C, D$ ，按下列要求作图（保留作图痕迹并标注相关字母）．

（1）画射线 $A B$ ；
（2）画直线 $A C$ ；
（3）连结 $D C$ ，并延长至点 $E$ ，使得 $C E = D C$ ；
（4）在直线 $A C$ 上找一点 $P$ ，使得 $P B + P D$ 最小．

查看试题解析
17. 计算。

(1)、 $38 ° 45^{'} + 72.5 ° 。$ (结果用度、分、秒表示)

(2)、 $58 ° 32^{'} 21^{'}' - 20 ° 42^{'} 44^{'}' 。$

查看试题解析
18. 在平整的地面上，有若干个完全相同棱长的小正方体堆成一个几何体，如图所示．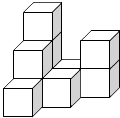

(1)、请画出这个几何体的三视图．

(2)、如果在这个几何体的表面喷上黄色的漆，则在所有的小正方体中，有个正方体只有一个面是黄色，有个正方体只有两个面是黄色，有个正方体只有三个面是黄色．

(3)、若现在你手头还有一些相同的小正方体，如果保持俯视图和左视图不变，最多可以再添加几个小正方体？

查看试题解析
19. 如图所示的几何体是由5个大小相同的小正方体搭成．

(1)、请在网格中画出这个几何体的主视图和左视图．

(2)、在这个几何体中，当去掉一个小正方体时，剩余部分的俯视图没有改变（填写图中小正方体的序号）；如果在这个几何体上再添加一些相同的小正方体，并保持这个几何体的主视图和左视图不变，那么最多可以再添加个小正方体．

查看试题解析
20. 十八世纪瑞士数学家欧拉证明了简单多面体的顶点数（ $V$ ）、面数（ $F$ ）、棱数（ $E$ ）之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单多面体模型，解答下列问题：

(1)、【观察总结】五种简单多面体的顶点数（ $V$ ）、面数（ $F$ ）、棱数（ $E$ ）如下表：
多面体
顶点数（ $V$ ）
面数（ $F$ ）
棱数（ $E$ ）
三棱锥
4
4
6
长方体
8
6
12
五棱柱
10
7
15
八面体
6
8
12
十二面体
20
12
30
猜想顶点数（ $V$ ）、面数（ $F$ ）、棱数（ $E$ ）之间存在的关系式是（用所给的字母表达）；

(2)、【简单应用】①能否组成一个有 $24$ 条棱、 $10$ 个面、 $13$ 个顶点的多面体？请说明理由．
②一个正二十面体有 $30$ 条棱，则它的顶点数是 ▲ ．

(3)、【实践探究】学校校园文化节，七年级数学实践小组同学制作了各种各样的多面体作品．
①一个多面体作品，只有 $12$ 个顶点，并且过每个顶点都有 $4$ 条棱，则这个多面体的面数是；
②一个多面体作品如图所示，每个面的形状是正三角形或正五边形，每条棱都是正三角形和正五边形的公共边，则该多面体作品正三角形比正五边形的面数多个．

查看试题解析

21. 【教材呈现】下图是华师版七年级上册数学教材第104页的部分内容

例5如图3.4.1所示的窗框，上半部分为半圆，下半部分为6个大小一样的长方形，长方形的长和宽的比为3：2．

设长方形的长为x米，用x表示所需材料的长度(重合部分忽略不计)

(1)、请根据教材提示，结合图3.4.1，写出例5中第(1)题完整的解题过程

(2)、【结论应用】图①、图②是某设计师设计的两种窗户设计图，图①是由边长4a正方形和直径4a半圆组成，图②是由一个八边形和直径2a的圆组成。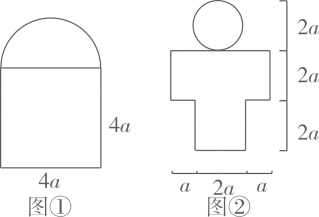

求图②的面积(用含有a的代数式表示，结果保留π)．

(3)、用铁丝做成图①、图②，这两个图形用的铁丝的长度是否相同，如果相同，请说明理由，如果不同，请比较出哪个设计图大?

查看试题解析

22. 【概念学习】点 $C$ 在线段 $A B$ 上，若 $\frac{A C}{A B} = a$ ，则称 $a$ 是点 $C$ 在线段 $A B$ 上的“分点值”，记作 ${(A \to B)}_{C} = a$ ．例如，如图1，若 $\frac{A C}{A B} = \frac{1}{3}$ ，则点 $C$ 在线段 $A B$ 上的“分点值”是 $\frac{1}{3}$ ，记作 ${(A \to B)}_{C} = \frac{1}{3}$ ；若 $\frac{B D}{A B} = \frac{2}{5}$ ，则 $\frac{A D}{A B} = \frac{3}{5}$ ，故点 $D$ 在线段 $A B$ 上的“分点值”是 $\frac{3}{5}$ ，记作 ${(A \to B)}_{D} = \frac{3}{5}$ ．

(1)、【理解与应用】已知点 $C$ 在线段 $A B$ 上．若 $A B = 9$ ， $A C = 4.5$ ，则 ${(A \to B)}_{C} =$ ；
若 $B C = 6$ ， ${(A \to B)}_{C} = \frac{2}{3}$ ，则 $A B =$ ．

(2)、如图2，线段 $A B = 24 c m$ ， $P$ 是线段 $A B$ 上一点， $C$ 、 $D$ 两点分别从点 $P$ 、 $B$ 出发以 $1 c m / s$ ， $2 c m / s$ 的速度同时向点 $A$ 运动，运动的时间为 $t s$ ，当其中一点到达点 $A$ 时，两点都停止运动．
①若点 $D$ 在 $P B$ 上运动时，总有 $P D = 2 A C$ ，求出 ${(A \to B)}_{P}$ 的值；
②若 ${(A \to B)}_{P} = \frac{1}{4}$ ，则当 $t$ 为何值时， ${(A \to P)}_{C} + {(P \to B)}_{D} = \frac{7}{6}$ ；
③若 $t = 7 s$ 时， $C D = 1 c m$ ，则 ${(A \to B)}_{P} =$ ▲ ．

查看试题解析
23. 综合与实践
某兴趣小组利用长为a 厘米，宽为b 厘米的长方形纸板制作长方体纸盒，做了以下尝试：（纸板厚度及接缝处忽略不计）

(1)、如图1，若 $a = b$ ，先在纸板四角剪去4个同样大小边长为c 厘米的小正方形，再沿虚线折起来就可以做成一个无盖的正方体纸盒．此时，b与c的数量关系为_______

(2)、如图2，若 $a = b$ ，先在纸板四角剪去4个同样大小边长为c 厘米的小正方形，再沿虚线折起来就可以做成一个无盖的长方体纸盒，为了使纸盒底面更加牢固且达到废物利用的目的，将剪下的四个小正方形平铺在盒子的底面，要求既不重叠又恰好铺满，此时，b与 c的数量关系为_______．

(3)、若 $a = 20 ， b = 12$ ，在纸板四角剪去4个同样大小边长为c 厘米的小正方形，恰好可以制作成一个无盖的长方体纸盒，请你通过列表研究，c取何整数时，所得长方体的体积V最大？
$c / cm$
1
2
3
4
5
$V / {cm}^{3}$
180
256
252
192
100

查看试题解析
24. 为了培养同学们的几何思维能力，张老师给同学们设置了一道几何题探究题：将一副三角尺按如图1所示位置摆放，三角尺ABC中，∠BAC=90°，∠B=∠C=45°；三角尺ADE中，∠E=90°， ∠DAE=60°， ∠D=30°，分别作∠BAE， ∠CAD的平分线AM，AN.试求出∠MAN的度数. 为了便于同学们探究，特别进行了以下活动：
[初步探究]现将三角尺按照图2，图3所示的方式摆放，AM，AN仍然是∠BAE， ∠CAD的平分线.在图2中AB与AD重合，在图3中AB，AE与AM重合在一起.

(1)、图2中∠MAN的度数为°，图3中∠MAN的度数为°.

(2)、[深入探究]通过初步探究，请你猜想图1中∠MAN的度数为 ▲ °.如果设∠BAD= $x$ ，请求出图1中∠MAN的度数.

查看试题解析

多面体	顶点数（ $V$ ）	面数（ $F$ ）	棱数（ $E$ ）
三棱锥	4	4	6
长方体	8	6	12
五棱柱	10	7	15
八面体	6	8	12
十二面体	20	12	30

$c / cm$	1	2	3	4	5
$V / {cm}^{3}$	180	256	252	192	100