-
1、为促进乡村振兴发展,某通讯公司计划在如图所示的三条街道AB,BC,AC两两相交所围成的 中,修建一个网络基站,让村民们获取消息更便捷.要求是基站位置到三条街道的距离均相等,请你找出这个基站合适的修建位置.(尺规作图,不写作法,保留作图痕迹)

-
2、如图,在 中, , D,E分别是CB,BC延长线上的点,且. 求证:

-
3、 如图,在四边形ABCD中,E,F分别是边AD,CD上的点,连接BE,BF,已知 若DE=3,则DF的长为.

-
4、如图,在 中,E是AB边上一点,F是 外一点,连接EF交AC于点D,连接CF,已知( 若D是AC的中点,AB=7,CF=2,则BE的长为

-
5、 如图,在△ABC中,AD平分∠CAB,DE⊥AB 于点E.若点D 到AC的距离为3,△ABD 的面积为9,则AB的长为.

-
6、 已知△ABC的三边长为3,2a+1,6,△DEF 的周长为14,若△ABC≌△DEF,则a的值为.
-
7、如图,虽然三角形被纸板挡住了一部分,但是小明仍能画出一个能与这个三角形完全重合的三角形,其数学依据是.

-
8、 如图,在△ABC中,AD平分∠BAC,E为AD 的中点,连接BE,AB:AC=3:2,若. 则△BDE的面积为 ( )
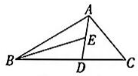 A、1 B、2 C、4 D、6
A、1 B、2 C、4 D、6 -
9、如图为6个边长相等的正方形组合成的图形,则∠1+∠2+∠3的度数为 ( )
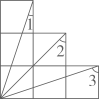 A、90° B、120° C、135° D、150°
A、90° B、120° C、135° D、150° -
10、如图是嘉嘉为参加手工比赛制作燕子风筝的骨架图,已知AC=AD,AB=AE,∠BAD=∠EAC,∠D=35°,则∠C的度数为 ( )
 A、30° B、35° C、40° D、45°
A、30° B、35° C、40° D、45° -
11、如图,在△ABC中,以点A为圆心,任意长为半径作弧,交AB 于点D,交AC 于点E,分别以点D,E为圆心,大于 的长为半径画弧,两弧交于点 F,连接AF交BC 于点 G,连接EG,且EG⊥AC,若EG=2,AB=6,则△ABG的面积为 ( )
 A、6 B、9 C、12 D、15
A、6 B、9 C、12 D、15 -
12、 如图,在△ABC中,∠ABC=90°,DE⊥AB 于点 E,交AC 于点 F,且DE=AB=4,连接BD,若BD=AC,BC=2,则AE的长为 ( )
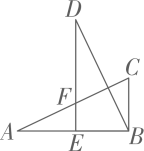 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5 -
13、如图,明明在湖一侧点A 处插上一面旗帜,然后绕到湖正对面点B处再插上一面旗帜,再从点 B 向东走60米到点 C 处,插上一面旗帜,继续向东走 60米到达点D 处后向南走50米到达点 E,此时恰好能看到A,C处的旗帜重合,则A,B两面旗帜间的距离为 ( )
 A、30米 B、50米 C、60米 D、80米
A、30米 B、50米 C、60米 D、80米 -
14、如图,下列三角形中,与△ABC全等的是 ( )
 A、
A、 B、
B、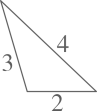 C、
C、 D、
D、
-
15、 如图,在四边形ABCD中,连接BD,已知AB=CB,若要用“SAS”判定△ABD≌△CBD,则还需添加的一个条件是 ( )
 A、∠ABD=∠CBD B、∠A=∠C C、AD=CD D、∠ADB=∠CDB
A、∠ABD=∠CBD B、∠A=∠C C、AD=CD D、∠ADB=∠CDB -
16、如图,△ABC≌△DFE,则下列说法中不一定正确的是 ( )
 A、∠A=∠D B、∠ACE=∠DEC C、AB=DF D、BE=DE
A、∠A=∠D B、∠ACE=∠DEC C、AB=DF D、BE=DE -
17、下列各组图形中,是全等形的是 ( )A、
 B、
B、 C、
C、 D、
D、
-
18、 在 中,AB=AC,D为BC的中点,E,F分别为AC,AB上的点,连接AD,DE,EF,FD.
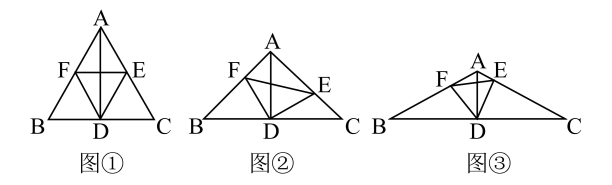 (1)、【探究发现】如图①,若AB=BC,F为AB的中点, 求证:AB=AF+AE;(2)、【类比猜想】如图②,若 , 试说明AB,AE,AF之间的数量关系;(3)、【拓展延伸】如图③,若 求AB 的长度.
(1)、【探究发现】如图①,若AB=BC,F为AB的中点, 求证:AB=AF+AE;(2)、【类比猜想】如图②,若 , 试说明AB,AE,AF之间的数量关系;(3)、【拓展延伸】如图③,若 求AB 的长度. -
19、如图, 是等腰三角形, 是等边三角形,且点B,D,E,C在同一条直线上.
 (1)、若AD=2,BC=12,求CE的长;(2)、以AC为腰在AC下方作等腰 使AF=AC,连接EF,BF.若BD=EF.求证: 是等边三角形.
(1)、若AD=2,BC=12,求CE的长;(2)、以AC为腰在AC下方作等腰 使AF=AC,连接EF,BF.若BD=EF.求证: 是等边三角形. -
20、如图,在 中, , 点 D,E分别在AB,BC上,且
 (1)、求 的度数;(2)、求证:BE=2AD.
(1)、求 的度数;(2)、求证:BE=2AD.