相关试卷

1、关于二次函数 $y = x^{2} + 2 x - 8 ，$ 下列说法中正确的是( )

A、图象的对称轴在 y 轴的右侧 B、图象与 y 轴的交点坐标为(0，8) C、图象与 x 轴的交点坐标为(-2，0)和(4，0) D、y 的最小值为-9

查看解析
2、如图，抛物线 $y = x^{2} + b x + c$ 经过点A(4，—5)，过点 A 分别向 x 轴、y轴作垂线，垂足分别为 B，C，得到矩形ABOC，且抛物线经过点 C.

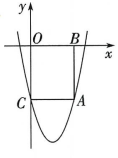(1)、求抛物线对应的函数表达式.

(2)、将抛物线绕直线x=a(0<a<2)翻转，分别交线段 OB，AC 于 D，E 两点.若直线DE 刚好平分矩形ABOC 的面积，求a 的值.

(3)、将抛物线旋转180°，使点 A 的对应点为A₁(m-2，n-4)，其中m≤2.若旋转后的抛物线仍然经过点 A，直接写出旋转后的抛物线的顶点达到最低点时的坐标.

查看解析
3、如图，抛物线 $y = - x^{2} + b x + c$ 经过点A(1，0)，B(0，5).

(1)、求这个抛物线对应的函数表达式.

(2)、设抛物线与x轴的另一交点为C，抛物线的顶点为 D，试求出点 C，D的坐标和△BCD的面积.

(3)、 P 是线段OC 上一点，过点 P 作PH⊥x轴，与抛物线交于点 H.是否存在点 P，使得线段 BC 把△PCH 分成面积相等的两部分?若存在，请求出点 P 的坐标；若不存在，请说明理由.

查看解析
4、如图，抛物线 $y = a x^{2} + b x + 3$ 与x 轴交于A，B两点，且点 B 的坐标为(2，0)，与y 轴交于点C，抛物线的对称轴为直线 $x = - \frac{1}{2} .$ 连结AC，BC，P是抛物线上在第二象限内的一个动点.过点P 作x轴的垂线PH，垂足为H，交AC 于点Q.过点 P 作PG⊥AC 于点G.求：

(1)、抛物线对应的函数表达式.

(2)、△PQG 周长的最大值及此时点 P 的坐标.

查看解析
5、如图，抛物线 $y = a x^{2} + 3 a x + c (a⟩ 0)$ 与y轴交于点C，与x 轴交于A，B 两点，点 A在点 B 左侧. 点 B 的坐标为(1，0)，OC=3OB，连结BC.

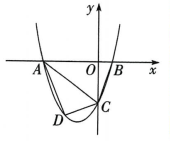(1)、求点C 的坐标.

(2)、求抛物线对应的函数表达式.

(3)、若D 是线段AC 下方抛物线上的动点，连结AD，CD，求四边形 ABCD 面积的最大值.

查看解析
6、如图，A，B两个带指针的转盘分别被分成三个面积相等的扇形，转盘 A 上的数分别是-6，-1，5，转盘 B 上的数分别是 6，-7，4(两个转盘除表面数不同外，其他完全相同).小聪和小明同时转动A，B两个转盘，使之旋转(规定：若指针恰好停留在分界线上，则重新转一次).

(1)、转动转盘，转盘 A 指针指向正数的概率是.

(2)、同时转动两个转盘，转盘 A 指针所指的数记为a，转盘 B 指针所指的数记为b.若a+b>0，则小聪获胜；若a+b<0，则小明获胜.请用列表法说明这个游戏是否公平.

查看解析
7、皮皮玩如图所示的迷宫游戏.他每遇到一扇门就从里面走出，然后随机左转或右转继续前行，规定走进死胡同算失败，那么皮皮从迷宫中心O 成功走出这个迷宫的概率为.

查看解析
8、看了《田忌赛马》的故事后，小杨用数学模型来分析：齐王与田忌的上、中、下三个等级的三匹马记分如下表，每匹马只赛一场，两数相比，大数为胜，三场两胜则赢.已知齐王的三匹马出场顺序为 10，8，6.若田忌的三匹马随机出场，则田忌能赢得比赛的概率为.

下等马
中等马
上等马
齐王
6
8
10
田忌
5
7
9

查看解析
9、一个小球在如图所示的方格地砖上任意滚动，并随机停留在某块地砖上，每块地砖的大小、质地完全相同，则该小球停留在涂色区域的概率是.

查看解析
10、小明将第一次掷出的骰子朝上的数字记为x，第二次掷出的骰子朝上的数字记为y(x与y分别取1，2，3，4，5，6中的一个数字)，则小明进行一次操作所获取的点 P(x，y)能落在二次函数 $y = - x^{2} + 4 x$ 图象上的概率为( )

A、 $\frac{1}{18}$ B、 $\frac{1}{12}$ C、 $\frac{1}{9}$ D、 $\frac{1}{6}$

查看解析
11、如图，电路图上有 4 个开关A，B，C，D 和1个小灯泡，在所有的元件和线路都正常的前提下，下列操作中，使得“小灯泡发光”这个事件是随机事件的为( )

A、只闭合1个开关 B、只闭合2个开关 C、只闭合3个开关 D、闭合4个开关

查看解析
12、数轴上表示 $a$ ， $b$ ， $c$ 的点如图所示，下列式子中正确的是（）

A、 $- a < c$ B、 $a + c < 0$ C、 $a > c > b$ D、 $b - a < 0$

查看解析
13、【阅读与思考】我们知道 $\sqrt{7}$ 是无理数，而无理数是无限不循环小数，因此 $\sqrt{7}$ 的小数部分我们不可能全部的写出来，而因为 $\sqrt{4} < \sqrt{7} < \sqrt{9}$ ，即 $2 < \sqrt{7} < 3$ ，于是 $\sqrt{7}$ 的整数部分是 $2$ ，将一个数减去其整数部分，差就是小数部分，故可用 $\sqrt{7} - 2$ 来表示 $\sqrt{7}$ 的小数部分．
结合以上材料，回答下列问题：

(1)、 $\sqrt{17}$ 的小数部分是______， $4 - \sqrt{6}$ 的整数部分是____；

(2)、如果 $\sqrt{5}$ 的小数部分为 $a$ ， $\sqrt{37}$ 的整数部分为 $b$ ，求 $a + b - \sqrt{5}$ 的值；

(3)、已知 $20 + \sqrt{21} = x + y$ ，其中 $x$ 是整数，且 $0 < y < 1$ ，请直接写出 $x + \sqrt{21} - y - 3$ 的平方根．

查看解析
14、方程 $x^{2} - 2 x - 24 = 0$ 的根是 $x_{1}$ ， $x_{2}$ ，则 $x_{1} x_{2}$ 的值为（）

A、2 B、 $- 2$ C、 $- 24$ D、24

查看解析
15、有一个数值转换器，原理如图所示，当输入x的值为16时，输出y的值为（）

A、1 B、2 C、 $\sqrt{2}$ D、 $\pm \sqrt{2}$

查看解析
16、比较大小： $- |- 4.25|$ $- (- 4 \frac{1}{4})$ ； $- \frac{1}{2}$ $- \frac{1}{3}$ （选填 $> ， = ， <$ ）

查看解析
17、如图在 $△ A B C$ 中， $A B$ 的垂直平分线 $D E$ 分别交 $B C$ 、 $A B$ 于点 $D$ 、点 $E$ ，连接 $A D$ ．若 $A E = 5 cm$ ， $△ A C D$ 的周长为 $16 cm$ ，则 $△ A B C$ 的周长为 $cm$ ．

查看解析
18、如图，某单位拟在一块空地上修建矩形植物园 $A B C D$ ，其中一边靠墙，可利用的墙长不超过 $16$ 米，另外三边由 $40$ 米长的栅栏围成，设矩形 $A B C D$ 中，垂直于墙的边 $A B = x$ 米，面积为y平方米．

(1)、若矩形 $A B C D$ 的面积为 $150$ 平方米，求x的值；

(2)、当矩形 $A B C D$ 的面积最大时，利用的墙长是多少米？并求此时的最大面积．

查看解析
19、解答下列各题

(1)、如图，在 $∠ A O B$ 中，以 $O$ 为顶点引射线，填表：
$∠ A O B$ 内射线的条数
$1$
$2$
$3$
$4$
角的总个数
______
______
______
_____

(2)、若 $∠ A O B$ 内射线的条数是 $n$ ，请用关于 $n$ 的式子表示出上面的结论．

(3)、若 $∠ A O B$ 内有射线条数是 $2024$ ，则角的总个数为多少？

查看解析
20、已知等腰三角形一边长为4，另两边恰好是关于 $x$ 的方程 $x^{2} - (m + 1) x + 2 (m - 1) = 0$ 的根，求此三角形的另两边长．

查看解析

上一页 440 441 442 443 444 下一页跳转

$∠ A O B$ 内射线的条数	$1$	$2$	$3$	$4$
角的总个数	______	______	______	_____

	下等马	中等马	上等马
齐王	6	8	10
田忌	5	7	9