4.4《一次函数的应用》（3）---北师版数学八年级上册课堂分层训练

试卷更新日期：2025-11-13 类型：同步测试

进入出卷网下载

一、基础夯实

1. 两条直线 $y_{1} = a x + b$ 与 $y_{2} = b x + a (a \neq 0, b \neq 0)$ 在同一平面直角坐标系中的图像可能是（）

A、 B、 C、 D、

查看试题解析
2. 如图，直线 $y = 2 x$ 与 $y = k x + b$ 相交于点 $P (1 ， 2)$ ，则关于 $x$ 的方程 $k x + b = 2 x$ 的解是（）

A、 $x = 4$ B、 $x = 2$ C、 $x = 1$ D、 $x =$ $\frac{1}{2}$

查看试题解析
3. 如图，已知A、B两地相距20km，甲从A地出发到B地，一段时间后，乙从B地出发到A地，甲、乙两人离A地的距离 $s (k m)$ 与甲所用的时间 $t (h)$ 之间的关系如图所示，则他们相遇时距离A地（）

A、8km B、10km C、12km D、14km

查看试题解析
4. 直线 $y = k x + b$ 平行于直线 $y = 2 x - 3$ ，且过点 $(0, - 1)$ ，则直线 $y = k x + b$ 的函数解析式是．

查看试题解析
5. 函数 $y = a x$ 和 $y = k x + b$ 的图象相交于点 $A (- 2, 1)$ ，则方程 $a x = k x + b$ 的解为．

查看试题解析
6. 如图是A，B两种手机套餐每月资费y(元)与通话时间x(分钟)对应的函数图象，若小红每月通话时间大约为500分钟，则从A，B两种手机资费套餐中选择套餐更合适．

查看试题解析
7. 长沙向北京打长途电话，设通话时间x(分)，需付电话费y(元)，通话3分以内话费为3.6元.请你根据如图所示的y随x的变化的图象，找出通话5分钟需付电话费元.

查看试题解析
8. 如图，l₁反映了某公司产品的销售收人与销售量的关系，l₂ 反映了该公司产品的销售成本与销售量的关系，根据图象判断：当该公司赢利（收入大于成本）时，销售量必须

查看试题解析
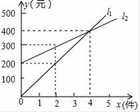9. 某校为了选拔百米运动员，让学生进行百米比赛，小明和小亮同时起跑，比赛情况如图所示，其中横轴表示时间t(s)，纵轴表示距起跑点的距离s(m)，根据图象回答下列问题.

(1)、小明和小亮的百米成绩各是多少？

(2)、两人的速度各是多少？

(3)、当小明到达终点时，小亮所跑的路程是多少？

查看试题解析
10. “生活即教育，行为即课程”．某校将劳动教育融入立德树人全过程．学校给每个班划分一块地供学生“种菜”，某班现要购买肥料对该地施肥，该班班长与农资店店主商量后，店主给出了两种购买方案（如表），且都送货上门．
方案
运费
肥料价格
方案一
12元
3元 $/ kg$
方案二
0元
3.6元 $/ kg$
若该班购买 $x$ 千克肥料，按方案一购买的付款总金额为 $y_{1}$ 元，按方案二购买的付款总金额为 $y_{2}$ 元．

(1)、请分别写出 $y_{1}, y_{2}$ 与 $x$ 之间的函数关系式；

(2)、若该班计划用180元钱购买肥料，请问该班选择哪种购买方案购买的肥料较多？

查看试题解析

二、能力提升

11. 快车从甲地匀速开往乙地，慢车从乙地出发沿同一条公路匀速前往甲地．慢车先出发1小时，快车再出发．设慢车行驶的时间为 $t$ 小时，两车之间的距离为 $y$ 千米， $y$ 与 $t$ 的函数关系如图所示．下列结论：①快车出发 $4.4$ 小时后两车相遇；②慢车的速度是100千米/小时；③线段 $A B$ 所在直线的函数表达式为 $y = 200 t - 1080$ ，正确的有（）

A、①② B、②③ C、①②③ D、①③

查看试题解析
12. 【素材1】某景区游览路线及方向如图甲所示，①④⑥各路段路程相等，⑤⑦⑧ 各路段路程相等，②③两路段路程相等.
【素材2】设游玩行走速度恒定，经过每个景点都停留20分钟，小温游路线①④ ⑤⑥⑦⑧用时3小时25分钟；小州游路线①②⑧，他离入口的路程s与时间t 的关系（部分数据）如图乙所示，在2100米处，他到出口还要走10分钟.
【问题】路线①③⑥⑦⑧各路段的路程之和为（）

A、4200米 B、4800米 C、5200米 D、5400米

查看试题解析
13. 清明期间，甲、乙两人同时登云雾山，甲、乙两人距地面的高度y（米）与登山时间x（分）之间的函数图象如图所示，且乙提速后乙的速度是甲的3倍．则下列说法错误的是（　　）

A、乙提速后每分钟攀登30米 B、乙攀登到300米时共用时11分钟 C、从甲、乙相距100米到乙追上甲时，乙用时 $6.5$ 分钟 D、从甲、乙相距100米到乙追上甲时，甲、乙两人共攀登了330米．

查看试题解析
14. A、B两地相距80km，甲、乙两人沿同一条路从A地到B地．l₁ ， l₂分别表示甲、乙两人离开A地的距离s（km）与时间t（h）之间的关系．对于以下说法：①乙车出发1.5小时后甲才出发；②两人相遇时，他们离开A地20km；③甲的速度是40km/h，乙的速度是 $\frac{40}{3}$ km/h；④当乙车出发2小时时，两车相距13km．其中正确的结论是（）

A、①③ B、①④ C、②③ D、②④

查看试题解析
15. A、B两地在一条笔直的公路上，甲从 A 地出发前往B 地，乙从 B 地出发前往 A 地，两人同时出发，甲到达 B 地后停止，乙继续前进到达A地.如图表示两人之间的距离y(米)与乙出发的时间x(分)间的函数关系，则下列结论中：①A、B 两地的距离是 1 200米；②两人出发4分相遇；③甲的速度是 100 米/分；④乙出发12分到达 A 地，正确的有.(填序号)

查看试题解析
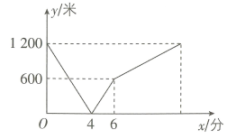16. 某工作室制作工艺品并出售，当工艺品的数量在60个以内时，该工作室制作的工艺品能全部售完.如图所示，线段AB，OC分别表示该工作室每天的制作成本y₁(元)，收入y₂(元)与销售量x(个)之间的函数关系.若该工作室某一天既不盈利也不亏损，则这天生产工艺品的个数是.

查看试题解析
17. 一个装有进水管和出水管的容器，开始时，先打开进水管注水，3分钟时，再打开出水管排水，8分钟时，关闭进水管，直至容器中的水全部排完.在整个过程中，容器中的水量 $y$ （升）与时间 $x$ （分）之间的函数关系如图所示，则图中 $a$ 的值为.

查看试题解析
18. 小明的爸爸和小明早晨同时从家出发，以各自的速度匀速步行上班和上学，爸爸前往位于家正东方的公司，小明前往位于家正西方的学校，爸爸到达公司后发现小明的数学作业在自己的公文包里，于是立即跑步去追小明，终于在途中追上了小明把作业给了他，然后再以先前的速度步行再回公司（途中给作业的时间忽略不计）．结果爸爸回到公司的时间比小明到达学校的时间多用了8分钟．如图是两人之间的距离y（米）与他们从家出发的时间x（分钟）的函数关系图，则小明家与学校相距米．

查看试题解析
19. 为响应国家“发展新一代人工智能”的号召，某市举办了无人机大赛．甲无人机从地面起飞，乙无人机从距离地面12米高的升降平台起飞，甲、乙两架无人机同时匀速上升，6秒时甲无人机到达大赛指定的高度停止上升开始表演，完成表演动作后，按原速继续飞行上升，当甲、乙两架无人机按照大赛要求同时到达距离地面的高度为72米时，进行联合表演．甲、乙两架无人机所在的位置距离地面的高度 $y$ （米）与飞行的时间 $x$ （秒）之间的函数关系如图所示．请根据图象回答下列问题：

(1)、甲无人机的速度是______米/秒，乙无人机的速度是______米/秒；

(2)、线段 $P Q$ 对应的函数表达式；

(3)、请直接写出当甲、乙两架无人机距离地面的高度差为9米时的时间．

查看试题解析
20. 已知小华家、文具店、书店依次在同一条直线上，文具店、书店离小华家的距离分别为 $1 k m, 1.6 k m$ ．小华从家出发，先匀速骑行 $8 m i n$ 到达书店，在书店停留了 $12 m i n$ ，之后匀速骑行 $3 m i n$ 到达文具店，在文具店停留 $7 m i n$ 后，再匀速骑行 $5 m i n$ 返回家．下面图中x表示时间，y表示离家的距离．图象反映了这个过程中小华离家的距离与时间之间的对应关系．
请根据相关信息，解答下列问题：

(1)、①填表：
小华离开家的时间/min
4
15
23
30
小华离家的距离/km
1
②填空：小华从文具店返回家的速度为_▲_ $k m / m i n$ ；
③当 $0 \leq x \leq 23$ 时，请直接写出小华离家的距离y关于时间x的函数解析式；

(2)、若小华的哥哥与小华同时离开书店，小华的哥哥匀速步行直接返回家，他到家的时间比小华到家的时间晚 $1 m i n$ ．在从书店返回家的过程中，对于同一个x的值，小华离家的距离为 $y_{1}$ ，小华的哥哥离家的距离为 $y_{2}$ ，当 $y_{1} > y_{2}$ 时，求x的取值范围（直接写出结果即可）．

查看试题解析

三、综合拓展

21. 已知甲、乙、丙三地依次在同一直线上，乙地离甲地260km，丙地离乙地160km.一艘游轮从甲地出发，途经乙地前往丙地.当游轮到达乙地时，一艘货轮沿着同样的线路从甲地出发前往丙地.已知游轮的速度为20km/h，离开甲地的时间记为t（单位：h），两艘轮船离甲地的距离y（单位：km）关于t的图象如图所示（游轮在停靠前后的行驶速度不变）.货轮比游轮早2.6h到达丙地.根据相关信息，解答下列问题：

(1)、填表：
游轮离开甲地的时间/h
6
13
16
22
24
游轮离甲地的距离/km
120
260

(2)、填空：
①游轮在乙地停靠的时长为h；
②货轮从甲地到丙地所用的时长为h，行驶的速度为km/h；
③游轮从乙地出发时，两艘轮船的距离为km.

(3)、当0≤t≤24时，请直接写出游轮离甲地的距离y关于t的函数解析式.

查看试题解析
22. 小敏和小慧去西湖风景区游玩，约好在少年宫广场见面。如图1，A地、B地、少年宫广场在一条直线上.小敏从A地出发，先匀速步行至车站，再坐公交车前往少年宫广场.同时，小慧从B地出发，骑车去少年宫广场，平均速度为200米/分钟.两人距离A地的路程s（米）和所经过的时间t（分）之间的函数关系如图2所示。（公交车的停车时间忽略不计）

(1)、求公交车的平均速度。

(2)、求同时出发后，经过多少时间小敏追上小慧.

(3)、在小敏坐公交车的过程中，当她与小慧相距400米时，求t的值.

查看试题解析

方案	运费	肥料价格
方案一	12元	3元 $/ kg$
方案二	0元	3.6元 $/ kg$

小华离开家的时间/min	4	15	23	30
小华离家的距离/km			1

游轮离开甲地的时间/h	6	13	16	22	24
游轮离甲地的距离/km	120		260

4.4《 一次函数的应用》（3）---北师版数学八年级上册课堂分层训练

一、基础夯实

二、能力提升

三、综合拓展

4.4《一次函数的应用》（3）---北师版数学八年级上册课堂分层训练