相关试卷

1、在平面直角坐标系中，以点A（3，0）为圆心， $\sqrt{13}$ 为半径作⊙A．直线y＝kx﹣3k+2与⊙A交于B，C两点，则BC的最小值为．

查看解析
2、我国南宋数学家秦九韶曾提出利用三角形的三边求面积的公式：一个三角形的三边长分别为a，b，c，三角形的面积S $= \sqrt{\frac{1}{4} [a^{2} b^{2} - {(\frac{a^{2} + b^{2} - c^{2}}{2})}^{2}]}$ .若a＝2 $\sqrt{2}$ ， b＝3，c＝1，则S的值为．

查看解析
3、如图，一块砖的A，B，C三个面的面积比是5：3：1．如果B面向下放在地上，地面所受压强为a Pa，那么C面向下放在地上时，地面所受压强为 Pa．

查看解析
4、把一根长10m的钢管截成3m长和1m长两种规格的钢管．为了不造成浪费，可能截得钢管的总根数为（写出一种情况即可）．

查看解析
5、南通是“建筑之乡”，工程建筑中经常采用三角形的结构．如图是屋架设计图的一部分，E是斜梁AC的中点，立柱AD，EF垂直于横梁BC．若AC＝4.8m，∠C＝30°，则EF的长为 m．

查看解析
6、分解因式am+a＝．

查看解析
7、在平面直角坐标系xOy中，五个点的坐标分别为A（﹣1，5），B（1，2），C（2，1），D（3，﹣1），E（5，5）．若抛物线y＝a（x﹣2）²+k（a＞0）经过上述五个点中的三个点，则满足题意的a的值不可能为（　　）

A、 $\frac{3}{8}$ B、 $\frac{4}{9}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看解析
8、如图，在等边三角形ABC的三边上，分别取点D，E，F，使AD＝BE＝CF．若AB＝4，AD＝x，△DEF的面积为y，则y关于x的函数图象大致为（　　）

A、 B、 C、 D、

查看解析
9、在△ABC中，∠C＝90°，tanA $= \frac{1}{2}$ ， AC＝2 $\sqrt{5}$ ，则BC的长为（　　）

A、1 B、2 C、 $\sqrt{5}$ D、5

查看解析
10、在平面直角坐标系xOy中，将点A（3，1）绕原点O逆时针旋转90°，得到点B，则点B的坐标为（　　）

A、（3，﹣1） B、（﹣1，3） C、（1，﹣3） D、（﹣3，1）

查看解析
11、如图是一个几何体的三视图（图中尺寸单位：cm），则这个几何体的底面圆的周长为（　　）

A、6πcm B、9πcm C、12πcm D、16πcm

查看解析
12、已知直线y＝kx+b经过第一、第二、第三象限，则k，b的取值范围是（　　）

A、k＜0，b＜0 B、k＜0，b＞0 C、k＞0，b＜0 D、k＞0，b＞0

查看解析
13、上午9时整，钟表的时针和分针构成的角的度数为（　　）

A、30° B、60° C、90° D、120°

查看解析
14、如图，将△ABC沿着射线BC平移到△DEF．若BC＝6，EC＝4，则平移的距离为（　　）

A、2 B、4 C、6 D、8

查看解析
15、《2025年中国卫星导航与位置服务产业发展白皮书》显示，去年我国卫星导航与位置服务产业总产值达5758亿元．将“5758亿”用科学记数法表示为（　　）

A、5.758×10¹⁰ B、5.758×10¹¹ C、0.5758×10¹² D、57.58×10¹⁰

查看解析
16、计算（﹣2）×（﹣3），正确的结果是（　　）

A、﹣5 B、5 C、﹣6 D、6

查看解析
17、已知点 $A (2, y_{1})$ ， $B (- 1, y_{2})$ ， $C (- 2, y_{3})$ 在函数 $y = x^{2} - 2 x - c$ 的图象上，则 $y_{1}, y_{2}, y_{3}$ 的大小关系是（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{1} > y_{3} > y_{2}$ C、 $y_{2} > y_{1} > y_{3}$ D、 $y_{3} > y_{2} > y_{1}$

查看解析
18、已知 $a$ ， $b$ 互为相反数， $m$ ， $n$ 互为倒数，则 $3 (a + b) - 2025 m n$ 的值为．

查看解析
19、（1）补全数轴；
（2）把表示右边各数的点画在数轴上； $- (- 2)$ ， $- |- 2.5|$ ， $\frac{1}{2}$ ， ${(- 1)}^{100}$
（3）用“ $<$ ”把这些数连接起来．

查看解析
20、在平面直角坐标系中，抛物线 $y = a x^{2} + b x + 3 (a \neq 0)$ 与x轴交于点A(-3，0)，B(1，0)，与 y轴交于点C，顶点为 D，连结AD.

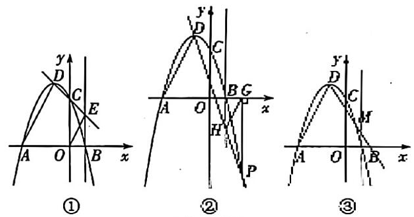(1)、 ① 如图①，直线CD 交直线.x=1于点E，连结OE.求证： $A D ‖ O E .$
②如图②，P(2，-5)为抛物线 $y = a x^{2} + b x + 3 (a \neq 0)$ 上一点，过点 P 作. $P G ⟂ x$ 轴，垂足为G.直线DP 交直线x=1于点 H，连结HG.求证： $A D ‖ H G .$

(2)、通过上述两种特殊情况的证明，你是否有所发现?请仿照(1)写出你的猜想，并证明，且在图③上画出草图.在平面直角坐标系中，抛物线 $y = a x^{2} + b x + 3 (a \neq 0)$ 与x轴交于点A(-3，0)，B(1，0)，顶点为 D，M为该抛物线上一动点(不与点A，B，D重合).

查看解析

上一页 383 384 385 386 387 下一页跳转