-
1、如图所示为某个几何体的三视图.
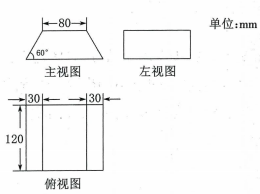 (1)、请描述这个几何体的形状.(2)、按三视图的实际尺寸,画出它的表面展开图(按10:1的比缩小).(3)、求这个几何体的侧面积和表面积.
(1)、请描述这个几何体的形状.(2)、按三视图的实际尺寸,画出它的表面展开图(按10:1的比缩小).(3)、求这个几何体的侧面积和表面积. -
2、如图,在一座大厦(BC)前面30m的地面上,有一盏地灯A 照射大厦,身高为1.6m 的小亮(EF)站在大厦与灯之间.小亮从现在所处的位置径直走向大厦,当他走到距离大厦只有5m 的点 D 处时停下.
 (1)、在图中画出此时小亮的位置(可用线段表示)及他在地灯照射下投在大厦BC 上的影子.(2)、求出此时小亮在地灯照射下投在大厦BC 上的影长.
(1)、在图中画出此时小亮的位置(可用线段表示)及他在地灯照射下投在大厦BC 上的影子.(2)、求出此时小亮在地灯照射下投在大厦BC 上的影长. -
3、如图所示的几何体是由棱长为a 的小立方体摆成的.
 (1)、请在网格中画出这个几何体的三视图.(2)、求这个几何体的表面积.
(1)、请在网格中画出这个几何体的三视图.(2)、求这个几何体的表面积. -
4、如图①②所示分别是两棵树及其影子的情形.
 (1)、哪个反映了路灯下的情形?哪个反映了阳光下的情形?(2)、你是用什么方法判断的?(3)、请分别画出图中表示小丽影长的线段.
(1)、哪个反映了路灯下的情形?哪个反映了阳光下的情形?(2)、你是用什么方法判断的?(3)、请分别画出图中表示小丽影长的线段. -
5、如图所示为放在地面上的一个长方体盒子,其中AB=9,BB'=5,B'C'=8,在线段 AB 的三等分点E(靠近点A)处有一只蚂蚁,线段B'C'的中点 F 处有一米粒,则蚂蚁沿长方体表面爬到米粒处的最短距离为.
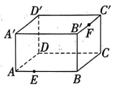
-
6、如图,正方形ABCD 的边长为8,以点A 为圆心,AD 长为半径画弧DE 得到扇形ADE(涂色部分,点E 在对角线AC上).若扇形 ADE 恰好是一个圆锥的侧面展开图,则该圆锥的底面半径是.
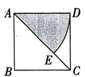
-
7、由8个相同的小正方体组成的几何体如图①所示,拿掉个小正方体后的几何体的主视图和左视图都是如图②所示的图形.
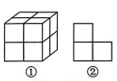
-
8、一个圆柱的表面积是336平方厘米,把它从中间切开,得到两个一样的圆柱,它们的表面积和是432平方厘米,那么原来圆柱的高约是厘米(π取3).
-
9、如图,在平面直角坐标系内,一点光源位于点A(0,5)处,线段CD 垂直于x轴,垂足为D,点C 的坐标为(3,1),则点C 的影子E 的坐标为.

-
10、一天上午,小红先参加了校运动会女子100m跑比赛,过一段时间又参加了女子400m跑比赛,如图所示为摄影师在同一位置拍摄的两张照片,则(填“甲”或“乙”)照片是参加400 m跑比赛时拍的.

-
11、如图所示为一个正方体,它的主视图是一个正方形,其面积为S1.若将这个正方体绕它的中心轴按逆时针方向旋转45°,观察者的位置不变,这时的主视图的面积为 S2 , 则S1:S2的值为( )
 A、 B、 C、1 D、2
A、 B、 C、1 D、2 -
12、 如图,圆锥的底面半径R=3cm,母线l=5cm,AB 为底面直径,C 为底面圆周上一点,∠COB=150°,D 为VB 上一点, 现在有一只蚂蚁,沿圆锥表面从点 C 爬到点D,则蚂蚁爬行的最短路程是( )
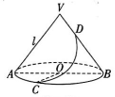 A、 B、 C、 D、
A、 B、 C、 D、 -
13、蒙古包可以近似地看作由圆锥和圆柱组成.如图所示为一个蒙古包的示意图,底面圆的半径DE=2m,圆锥的高AC=1.5m,圆柱的高CD=2.5m,则下列说法中,错误的是( )
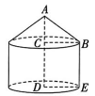 A、圆柱的底面积为4πm2 B、圆柱的侧面积为 C、圆锥的母线AB 的长为2.25m D、圆锥的侧面积为
A、圆柱的底面积为4πm2 B、圆柱的侧面积为 C、圆锥的母线AB 的长为2.25m D、圆锥的侧面积为 -
14、如图,将一张边长为6的正方形纸片按虚线裁剪后,恰好围成一个底面是正三角形的棱柱.这个棱柱的侧面积为( )
 A、36 B、 C、 D、
A、36 B、 C、 D、 -
15、如图,一个几何体上半部分为正四棱锥,下半部分为正方体,且有一个面涂有颜色,该几何体的表面展开图是( )
 A、
A、 B、
B、 C、
C、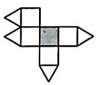 D、
D、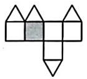
-
16、如图所示的三视图对应的几何体是( )
 A、
A、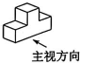 B、
B、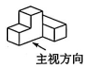 C、
C、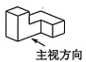 D、
D、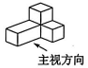
-
17、斗拱是我国古典建筑上的重要部件.如图所示为一种斗拱“三才升”的示意图及其主视图,则它的左视图为( )
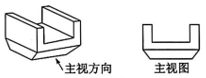 A、
A、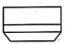 B、
B、 C、
C、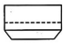 D、
D、
-
18、四块直立在地面上的字母广告牌在不同情况下,在地面上的投影(涂色部分)效果如图所示.在字母L,K,C的投影中,与字母N属同一种投影的有( )
 A、L,K B、C C、K D、L,K,C
A、L,K B、C C、K D、L,K,C -
19、下列投影中,不属于中心投影的是( )A、晚上路灯下小孩的影子 B、汽车灯照射下行人的影子 C、阳光下人的影子 D、舞台灯光下演员的影子
-
20、如图①,在正方形ABCD 中,点F,H 分别在边AD,AB上,连结AC,FH,CF,CH,AC 与FH 交于点E,(CF=CH.
 (1)、AC 与FH 垂直吗?请说明理由.(2)、 如图②,过点A,H,F 的圆交CF 于点P,连结PH,交AC 于点K.求证:(3)、在(2)的条件下,当K 为线段AC 的中点时,求 的值.
(1)、AC 与FH 垂直吗?请说明理由.(2)、 如图②,过点A,H,F 的圆交CF 于点P,连结PH,交AC 于点K.求证:(3)、在(2)的条件下,当K 为线段AC 的中点时,求 的值.