-
1、如图,已知 和线段a,b,若 利用直尺和圆规作 C(保留作图痕迹,不写作法)

-
2、如图,点C,D在线段BE上,BD=EC,AB=FE,AC=FD.求证:∠B=∠E.

-
3、 如图, O 为AC 上一点,BO 和 DO 分别平分∠ABD 和∠BDC,若BD=8,AB=3,则CD的长度为

-
4、 如图,△ABC和△ADE均为直角三角形,. AD=DE,点D在AC上,连接BE,与AC交于点 F,且F恰好为DC的中点,若BC=5,CF=3,则△ABC的面积为

-
5、 如图,将 绕点C顺时针旋转得到△DEC,其中点E恰好落在AC边上,若 , 则∠BCD 的度数是.

-
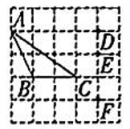
6、 如图,在5×5的正方形网格中, 的顶点均在格点上,若 , 则点 P 与点重合.(填“D”“E”或“F”,且点D,E,F均为格点)
-
7、如图,已知 欲说明 , 则可以补充的条件是.(写出一个即可)

-
8、如图,将等腰直角 放入平面直角坐标系中,已知 若点A 的坐标为(0,3),点B的坐标为(2,0),则点 C的坐标为 ( )
 A、(6,2) B、(5,2) C、(4,2) D、(3,2)
A、(6,2) B、(5,2) C、(4,2) D、(3,2) -
9、如图,在 中,BO,CO 分别平分 和 于点D,已知 的面积是21,(OD=3,则 的周长为 ( )
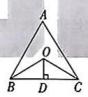 A、10 B、12 C、14 D、16
A、10 B、12 C、14 D、16 -
10、如图,将 沿直线DE折叠,点A 落在BC 的延长线点 F 处,若 则 的度数为( )
 A、 B、50 C、 D、
A、 B、50 C、 D、 -
11、如图①,已知 小聪想作一个 使得 , 其作图步骤如图②所示,下列说法错误的是 ( )
 A、第一步作图:在直线l上取一点E,以点E为圆心,BC长为半径作弧,与直线l交于点F B、小聪作图判定 的依据是SAS C、第二步作图是过点 E作直线l的垂线 D、小聪作图判定 的依据是HL
A、第一步作图:在直线l上取一点E,以点E为圆心,BC长为半径作弧,与直线l交于点F B、小聪作图判定 的依据是SAS C、第二步作图是过点 E作直线l的垂线 D、小聪作图判定 的依据是HL -
12、 如图,AD平分∠BAC,AB=AC,连接BD,CD 并延长分别交AC,AB于点 F,E,则此图中全等三角形的对数为 ( )
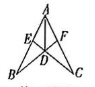 A、5对 B、4对 C、3对 D、2对
A、5对 B、4对 C、3对 D、2对 -
13、城市公园是城市生态系统的重要组成部分,是满足城市居民休闲、游览、锻炼的场所.桥梁横跨碧波之上,不仅是通行的纽带,更是艺术的绽放.请完成第4~5题:(1)、如图,某公园决定在湖两侧的A,B间架桥,要想测量A,B两点的距离,某工程队找一处看得见A,B的点 P,连接AP并延长到D,使PA=PD,连接BP并延长到C,使PC=PB,测得CD的长,即为A,B之间的距离.判断△ABP≌△DCP最直接的依据是 ( )
 A、SSS B、AAS C、SAS D、ASA(2)、如图是一座斜拉桥的剖面图,BC 是桥面,AD 是桥柱,设计时要保证桥柱和桥面是垂直的,且两根钢绳AB,AC 与桥面的夹角相等,则下列选项中正确的是 ( )
A、SSS B、AAS C、SAS D、ASA(2)、如图是一座斜拉桥的剖面图,BC 是桥面,AD 是桥柱,设计时要保证桥柱和桥面是垂直的,且两根钢绳AB,AC 与桥面的夹角相等,则下列选项中正确的是 ( ) A、AB=AC B、AB⊥AC C、AB>AC D、AB<AC
A、AB=AC B、AB⊥AC C、AB>AC D、AB<AC -
14、根据下列条件,能画出唯一△ABC 的是 ( )A、∠A=35°,∠B=60°,∠C=85° B、∠A=∠B=50°,AB=3 C、AB=4,AC=3,∠B=20° D、∠C=90°,AC=5
-
15、 如图,AE=AC,∠1=∠2,若要用“ASA”证明△ABC≌△ADE,则还需要添加的条件是( )
 A、∠B=∠D B、∠1=∠D C、∠E=∠C D、∠2=∠C
A、∠B=∠D B、∠1=∠D C、∠E=∠C D、∠2=∠C -
16、 已知△ABC≌△DEF,AB=3,则DE的长为 ( )A、3 B、4 C、5 D、6
-
17、【积累经验】我们在第十四章《全等三角形》中学习了全等三角形的性质和判定,在一些探究题中经常用以上知识转化角和边,进而解决问题.例如:我们在解决:“如图①,在 中, 线段DE 经过点 C,且. 于点 D, 于点E.求证:AD=CE,CD=BE.”这个问题时,只要证明 即可得到解决.
 (1)、请写出证明过程:(2)、【类比应用】如图②, 在平面直角坐标系中,A为x轴上一点, 点 B的坐标为(0,1),点C的坐标为((-4,4),求点A 的坐标;(3)、【拓展提升】如图③,在平面直角坐标系中,点A(2,0),点B(5,1)均在小正方形网格格点上,以AB为一边构造等腰直角 , 请直接写出第一象限内满足条件的所有点 C 的坐标.
(1)、请写出证明过程:(2)、【类比应用】如图②, 在平面直角坐标系中,A为x轴上一点, 点 B的坐标为(0,1),点C的坐标为((-4,4),求点A 的坐标;(3)、【拓展提升】如图③,在平面直角坐标系中,点A(2,0),点B(5,1)均在小正方形网格格点上,以AB为一边构造等腰直角 , 请直接写出第一象限内满足条件的所有点 C 的坐标. -
18、某政府计划购置如下图所示的单枪、双枪两款新能源充电桩,来满足新能源汽车车主日益增长的充电需求,购置充电桩的相关信息如下表.
单枪充电桩
双枪充电桩
花费:40000元
花费:30000元
单价:x元/个
单价:1.5x元/个
 (1)、若本次购买单枪充电桩的数量比双枪充电桩的数量多4个,求单枪、双枪两款新能源充电桩的单价;(2)、在(1)的条件下,根据游客需求,政府决定再次购进单枪、双枪两款新能源充电桩共6个,已知单枪新能源充电桩的单价比上次购买时提高了10%、双枪新能源充电桩的单价比上次购买时降低了10%,如果此次加购政府预备支出不超过35 500元,求政府最少需要购买单枪新能源充电桩的数量、
(1)、若本次购买单枪充电桩的数量比双枪充电桩的数量多4个,求单枪、双枪两款新能源充电桩的单价;(2)、在(1)的条件下,根据游客需求,政府决定再次购进单枪、双枪两款新能源充电桩共6个,已知单枪新能源充电桩的单价比上次购买时提高了10%、双枪新能源充电桩的单价比上次购买时降低了10%,如果此次加购政府预备支出不超过35 500元,求政府最少需要购买单枪新能源充电桩的数量、 -
19、如图,在 中,AB=AC,点E在CA的延长线上, , 垂足为P,EP交AB于点 F.
 (1)、求证: 是等腰三角形;(2)、若F是AB的中点,PF=3,求EF的长.
(1)、求证: 是等腰三角形;(2)、若F是AB的中点,PF=3,求EF的长. -
20、 “整体思想”法,即把多项式中的某些部分看成一个整体,用一个新的字母进行替代,可以简化多项式的结构,使因式分解更简洁明了.
例如:分解因式
解:将a-2b看成一个整体,令a-2b=x,则原式 将x还原得,原式
请根据上述材料回答下列问题:
(1)、请补全横线上的步骤:;(2)、因式分解: