浙教版数学八年级上学期重难点复习1:三角形中线、高线的应用
试卷更新日期:2025-09-10 类型:复习试卷
一、三角形的中线与周长
-
1. 等腰三角形一腰上的中线把这个三角形的周长分成两部分,已知这个等腰三角形的周长为 , 则这个等腰三角形的底边为( ) .A、8 B、20 C、40 D、8或402. 等腰三角形一腰上的中线把这个三角形的周长分成12cm和21cm两部分,则这个等腰三角形底边的长为cm.3. 已知是的中线,若与的周长分别为 , , 则 .4. 如图,在△ABC中,AD是BC边上的中线。已知 5cm,求△ABD与△ACD的周长的差。
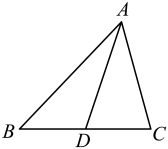 5. 【问题背景】小李同学在学习了数学第13章内容后,他对三角形的三边关系及三角形的中线特别感兴趣,下面是他总结的一些题目笔记.请同学们帮他分析.
5. 【问题背景】小李同学在学习了数学第13章内容后,他对三角形的三边关系及三角形的中线特别感兴趣,下面是他总结的一些题目笔记.请同学们帮他分析.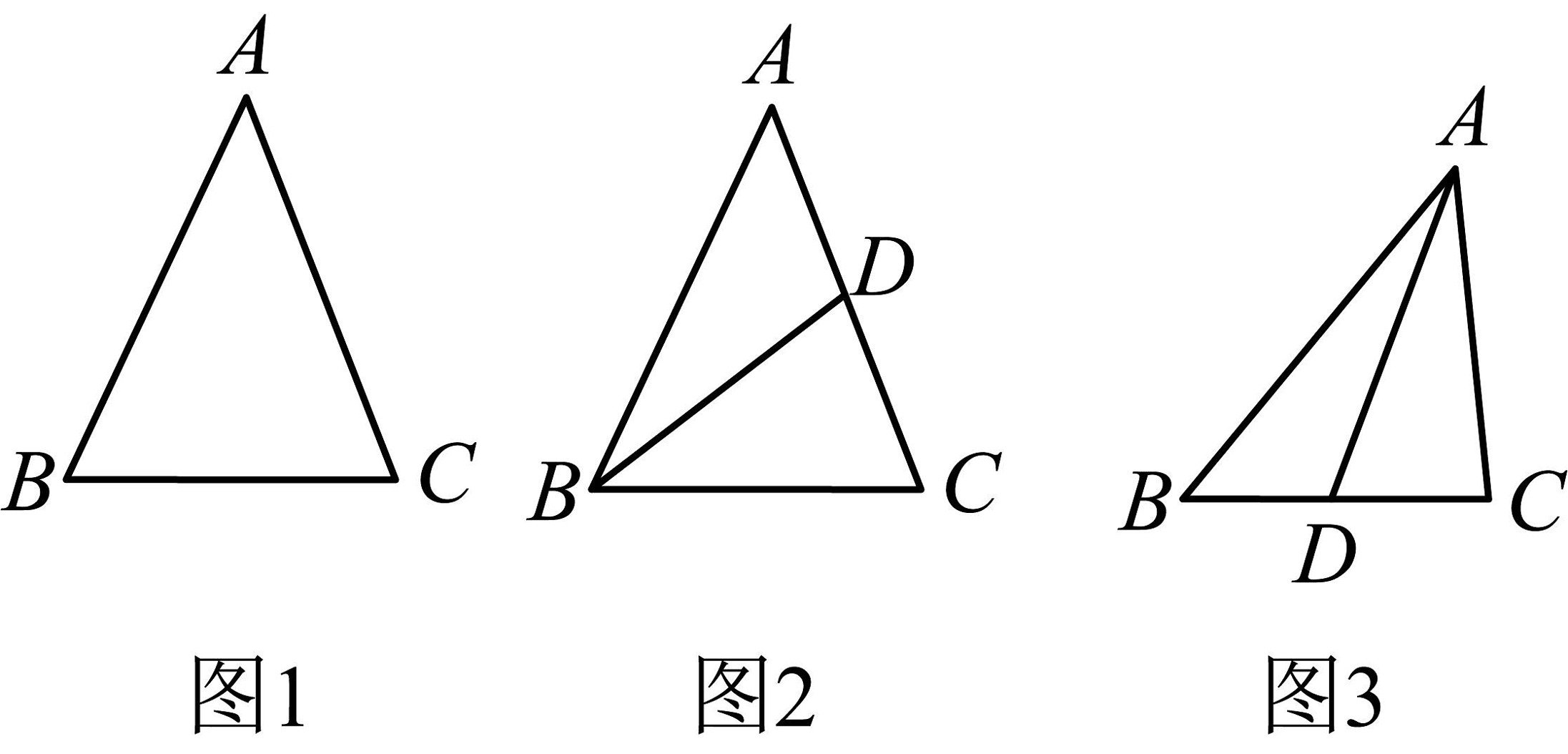
【新知探究】如图1,在等腰中,、是的腰.已知三角形两条边的长度分别为 , , 求的周长?小李经过计算,得出的的周长是或 .
任务1:小李的答案是否正确?如果不正确请写出正确的答案.
【新知拓展】根据【任务1】的答案,小李继续探索三角形中线的重要作用.
如图2,当添加条件:是等腰的中线时.求与的周长差.
任务2:请你帮小李写出解答过程.
【拓展应用】结合【任务2】的解答过程,小李继续探索三角形中线在一般三角形中是否具有同样作用.
如图3,在中,已知是的中线(且),其中 , . 则与的周长差是多少.
任务3:请用含 , 的代数式表示与的周长差.
二、三角形的中线与面积
-
6. 如图,的中线交于点 , 若阴影部分的面积是 , 则的面积是( )
 A、 B、 C、 D、7. 已知一个直角三角形的周长是4+2 , 斜边上中线长为2,则这个三角形的面积为( )A、5 B、2 C、 D、18. 如图所示,是的中线,点E是的中点,连接、 , 若的面积为16,则阴影部分的面积为 .
A、 B、 C、 D、7. 已知一个直角三角形的周长是4+2 , 斜边上中线长为2,则这个三角形的面积为( )A、5 B、2 C、 D、18. 如图所示,是的中线,点E是的中点,连接、 , 若的面积为16,则阴影部分的面积为 . 9. 如图,BD是△ABC的中线,CE是ABCD的中线,DF是△CDE的中线,若△ABC的面积为4.则△DEF 的面积为
9. 如图,BD是△ABC的中线,CE是ABCD的中线,DF是△CDE的中线,若△ABC的面积为4.则△DEF 的面积为 10. 综合与实践
10. 综合与实践【知识生成】三角形的中线把三角形分成面积相等的两部分.
已知:如图1,在△ABC中,点D是BC边上的中点,连接AD . 求证:S△ABD=S△ACD .
证明:过点A作AE⊥BC于E
∵点D是BC边上的中点
∴BD=CD
∵
∴S△ABD=S△ACD

【拓展探究】
(1)、如图2,在△ABC中,点D是BC边上的中点,若S△ABC=6,S△ABD=;(2)、如图3,在△ABC中,点D是BC边上的点且CD=2BD , S△ABD和S△ABC存在怎样的数量关系?请模仿写出证明过程;(3)、【问题解决】现在有一块四边形土地ABCD(如图4),熊大和熊二都想问老熊要这块地,老熊让他们平分,可他们谁都没法平分,请你来帮帮忙.
要求:用不超过三条的线段画出平分方法,并对作法进行描述.可利用带刻度的直尺.
三、等面积法的应用
-
11. 如图,中,AD是角平分线,BE是的中线,若的面积是24, , , 则的面积是( )
 A、15 B、12 C、7.5 D、612. 如图,在中, , , 是高,是中线,是角平分线,交于点 , 交于点 , 下面结论:①的面积的面积;②;③;④ .
A、15 B、12 C、7.5 D、612. 如图,在中, , , 是高,是中线,是角平分线,交于点 , 交于点 , 下面结论:①的面积的面积;②;③;④ .其中正确的结论是( )
 A、①② B、①②④ C、①②③ D、①②③④13. 如图,在中,是的中线,点E在上,点F在的延长线上,与交于点O , 且 .
A、①② B、①②④ C、①②③ D、①②③④13. 如图,在中,是的中线,点E在上,点F在的延长线上,与交于点O , 且 .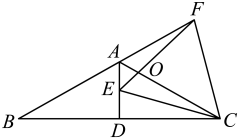 (1)、求证:;(2)、若 , 求证:14. 已知,在等边三角形 中, 为 边上的高.
(1)、求证:;(2)、若 , 求证:14. 已知,在等边三角形 中, 为 边上的高.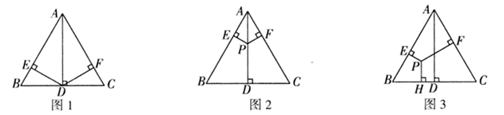 (1)、操作发现:如图1,过点 分别作 , ,垂足分别为 .请直接写出 和 的数量关系;(2)、如图2,若点 为 上任意一点(不与 重合),过点 作 , ,垂足分别为 .判断 和 的数量关系,并说明理由;(3)、拓广探索:
(1)、操作发现:如图1,过点 分别作 , ,垂足分别为 .请直接写出 和 的数量关系;(2)、如图2,若点 为 上任意一点(不与 重合),过点 作 , ,垂足分别为 .判断 和 的数量关系,并说明理由;(3)、拓广探索:如图3,点 为等边三角形 内任意一点,过点 作 , , ,垂足分别为 ,探究 和 的数量关系,并说明理由.
15. 如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高. (1)、当D点在BC的什么位置时,DE=DF?请说明理由.(2)、DE,DF,CG的长之间存在着怎样的等量关系?并说明理由.(3)、若D在底边BC的延长线上,(2)中的结论还成立吗?若不成立,又存在怎样的关系?并说明理由.16. 数学中常常利用面积相等来证明其他的线段相等,这种方法被称为“面积法”。已知等边△ABC , 点P是平面上任意一点,设点P到△ABC边AB、AC边的距离分别为PD、PE , △ABC的BC边上的高为AM.回答以下问题:
(1)、当D点在BC的什么位置时,DE=DF?请说明理由.(2)、DE,DF,CG的长之间存在着怎样的等量关系?并说明理由.(3)、若D在底边BC的延长线上,(2)中的结论还成立吗?若不成立,又存在怎样的关系?并说明理由.16. 数学中常常利用面积相等来证明其他的线段相等,这种方法被称为“面积法”。已知等边△ABC , 点P是平面上任意一点,设点P到△ABC边AB、AC边的距离分别为PD、PE , △ABC的BC边上的高为AM.回答以下问题: (1)、如图(1)若点P在三角形的BC边上,PD、PE、AM存在怎样的数量关系?请给出证明过程。(2)、如图(2),当点P在△ABC内,已知AM=10,求PD+PE+PF的值。(3)、如图(3),当点P在△ABC外,请直接写出AM与PD、PF、PE的数量关系,不用证明。
(1)、如图(1)若点P在三角形的BC边上,PD、PE、AM存在怎样的数量关系?请给出证明过程。(2)、如图(2),当点P在△ABC内,已知AM=10,求PD+PE+PF的值。(3)、如图(3),当点P在△ABC外,请直接写出AM与PD、PF、PE的数量关系,不用证明。四、分类讨论思想在三角形高线问题中的应用
-
17. 中, , 边上的高 , , 则的面积是( )A、 B、 C、或 D、以上都不对