3.1 代数式提升课时卷-北师大版数学七年级上册

试卷更新日期：2025-09-10 类型：同步测试

进入出卷网下载

一、选择题

1. 下列各式中，符合代数式书写规则的是（）

A、 $- 2 \frac{1}{6} p$ B、 $a \times \frac{1}{4}$ C、 $\frac{7}{3} x^{2}$ D、 $2 y \div x$

查看试题解析
2. 买一个足球需 $m$ 元，买一个篮球需 $n$ 元，则买4个足球和7个篮球共需（）元．

A、 $11 m n$ B、 $28 m n$ C、 $4 m + 7 n$ D、 $7 m + 4 n$

查看试题解析
3. 已知 $a - 2 b = 3$ ，则 $2 a - 4 b - 3$ 的值为（）

A、0 B、3 C、6 D、 $- 3$

查看试题解析
4. 若代数式 $- x ² + 3 x$ 的值为-2，则 $2 x ² - 6 x + 7$ 的值为 ( )

A、3 B、5 C、9 D、11

查看试题解析
5. 如图，现有五张图 1 所示形状大小完全相同的小长方形，长为 $a$ ，宽为 $b$ ，将它们放入图 2 的大长方形 $A B C D$ 中，若未被覆盖的两个阴影部分的周长分别记为 $C_{1}$ 和 $C_{2}, C_{1}$ 与 $C_{2}$ 的差等于两倍的小长方形的宽，则小长方形的长与宽满足（）

A、 $a = \frac{7}{2} b$
B、 $a = 3 b$
C、 $a = \frac{5}{2} b$
D、 $a = 2 b$

查看试题解析
6. 如图所示的运算程序中，若开始输入的x 值为48，我们发现第一次输出的结果为24，第二次输出的结果为12……则第2010 次输出的结果为( ).

A、6 B、3 C、 $\frac{3}{2^{2006}}$ D、 $\frac{3}{2^{1003}}$

查看试题解析
7. 当 $x = - 1$ 时，式子 $a x^{3} - b x + 1$ 的值为2025，则当 $x = 1$ 时，式子 $a x^{3} - b x + 1$ 的值为（）

A、2020 B、 $- 2021$ C、 $- 2022$ D、 $- 2023$

查看试题解析
8. 如 $M = {1, 2, x}$ ，我们叫集合M，其中1、2、x叫做集合M的元素．集合中的元素具有确定性（如x必然存在），互异性（如 $x \neq 1$ ， $x \neq 2$ ）（即改变元素的顺序，集合不变）．若集合 $N = {x, 1, 2}$ ，则我们说 $M = N$ ．已知集合 $A = \{2, 0, x\}$ ，集合 $B = \{\frac{1}{x}, |x|, \frac{y}{x}\}$ ，若 $A = B$ ，则则 $x - y$ 的值是（　　）

A、2 B、 $\frac{1}{2}$ C、 $- 2$ D、 $- 1$

查看试题解析

二、填空题

9. 多项式 $x^{4} y^{2} - x^{2} y + 2 y^{4}$ 的次数是．

查看试题解析
10. 若代数式 $x^{2} - 3 x - 2 = 5$ ，则代数式 $2021 + 9 x - 3 x^{2}$ 值是．

查看试题解析
11.

(1)、若a-2b=3，则9-2a+4b的值为.

(2)、当x=1 时，代数式 $\frac{1}{2} a x^{3} - 3 b x + 4$ 的值是7，则当x=-1时，这个代数式的值为.

查看试题解析
12. 若已知 $\frac{a}{3} - \frac{b}{2} = 1$ ，则代数式1-2a+3b的值为.

查看试题解析
13. 下列说法中： $①$ 倒数等于本身的数一定是 $1$ ； $②$ 若 $a$ 是实数，则 $a^{2} + 1$ 一定是正数； $③$ 如果一个数的绝对值等于它本身，那么这个数一定是非负数； $④$ 有理数分为正有理数和负有理数； $⑤$ 单项式 $- 2 π a^{2} b$ 的系数是 $- 2$ ； $⑥$ 多项式 $3^{2} a^{3} + 4 a^{2} - 8$ 的次数是 $3$ 次．其中正确的有（填写序号）．

查看试题解析

三、解答题

14. 下列整式哪些是单项式，哪些是多项式?它们的次数分别是多少?

(1)、7y²；

(2)、 $4 x y^{2};$

(3)、 35abc；

(4)、3x+5y；

(5)、 $1 + s^{2} + s t;$

(6)、 $\frac{4}{5} a^{2} x - a^{2} x^{3} + \frac{1}{5} x 。$

查看试题解析
15. 已知：a ， b互为相反数，c ， d互为倒数，x的绝对值是2，求

(1)、直接写出 $a + b$ ， $c d$ ， x的值．

(2)、求 $(a + b) x^{2} + (- c d)^{2015}$ 的值．

查看试题解析
16. 若 $|3 x + 1|$ 与 ${(y + 1)}^{2}$ 是互为相反数，求：

(1)、 $x y$ 的值；

(2)、 $- x^{3} - y^{100}$ 的值．

查看试题解析
17. 在学习一个数的绝对值过程中，化简 $|a|$ 时，可以这样分类：
当 $a > 0$ 时， $|a| = a$ ；当 $a = 0$ 时， $|a| = 0$ ；当 $a < 0$ 时， $|a| = - a$ ．请用这种方法解决下列问题．

(1)、当 $a = 3$ 时，则 $\frac{a}{|a|} =$ _____；当 $a = - 2$ 时，则 $\frac{a}{|a|} =$ _____．

(2)、当 $a = 4$ 时，则 $\frac{a}{|a|} =$ _____；当 $a = - 4$ 时，则 $\frac{a}{|a|} =$ _____．

(3)、你可以再找些数字代入 $a$ ，通过计算找到规律(不用写出规律)，并解决下列问题：已知 $a$ ， $b$ 是有理数，当 $a b > 0$ 时，试求 $\frac{a}{|a|} + \frac{b}{|b|}$ 的值．

查看试题解析
18. 如图是一个“数值转换机”（箭头是指某数进入转换机的路径，方框是对进入的数进行转换的转换机）．

(1)、当小明输入4，7这两个数时，两次输出的结果依次为________，________；

(2)、当输入的数为________时（写出2个），其输出结果为0；

(3)、这个“数值转换机”不可能输出________数．

(4)、若输出的结果是2，小明输入的正整数是________．（用含自然数 $n$ 的式子表示）．

查看试题解析
19. 小红准备将新购买的房子的地面铺上地砖，地面结构如图所示，根据图中所给的数据（单位：米），解答下列问题：

(1)、用含m，n的代数式表示地面的总面积；

(2)、已知 $n = 1.5$ 米，且客厅面积是卫生间面积的9倍，如果铺1平方米地面用地砖的平均费用为200元，那么小红家铺地面用地砖的总费用是多少元？

查看试题解析
20. 综合与实践
某兴趣小组利用长为a厘米，宽为b厘米的长方形纸板制作长方体纸盒，做了以下尝试：（纸板厚度及接缝处忽略不计）

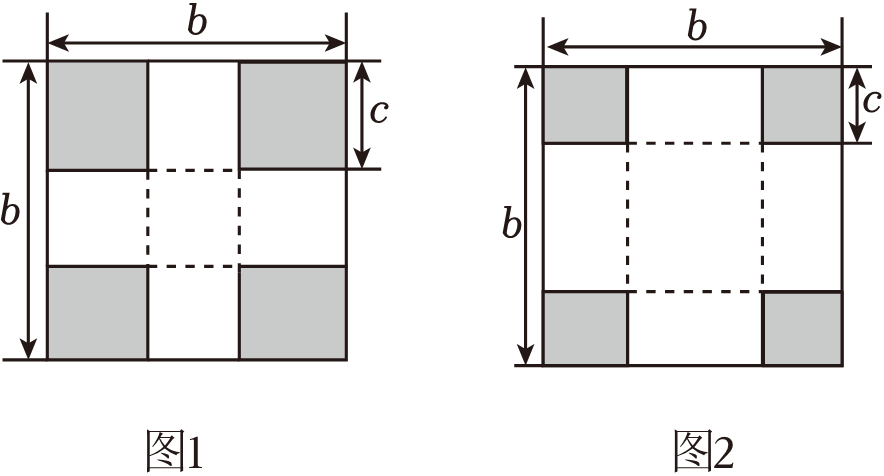(1)、如图1，若a=b，先在纸板四角剪去4个同样大小边长为c厘米的小正方形，再沿虚线折起来就可以做成一个无盖的正方体纸盒．此时，b与c的数量关系为．

(2)、如图2，若a=b，先在纸板四角剪去4个同样大小边长为c厘米的小正方形，再沿虚线折起来就可以做成一个无盖的长方体纸盒，为了使纸盒底面更加牢固且达到废物利用的目的，将剪下的四个小正方形平铺在盒子的底面，要求既不重叠又恰好铺满．此时，b与c的数量关系为．

(3)、若a=20，b=12，在纸板四角剪去4个同样大小边长为c厘米的小正方形，恰好可以制作成一个无盖的长方体纸盒．请你通过列表研究，c取何整数时，所得长方体的体积V最大？
c/cm

V/cm³

查看试题解析

c/cm
V/cm³