浙教版数学八年级上学期重难点复习2:尺规作图
试卷更新日期:2025-09-11 类型:复习试卷
一、尺规作一个角等于已知角
-
1. 下面是作业本上的一道习题,小可,小雨,小齐,小梦四位同学的作法中,错误的是( )
题目:
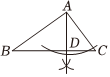
如图,在△ABC 中,∠B=80°,∠C=40°,借助尺规,在直线AC 上找一点 D,连接 BD,使得∠CBD=∠C.
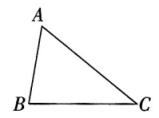 A、
A、 小可的作法
B、
小可的作法
B、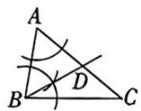 小雨的作法
C、
小雨的作法
C、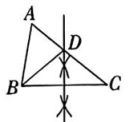 小齐的作法
D、
小齐的作法
D、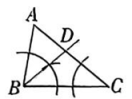 小梦的作法
2. 如图,已知一个点O,请用尺规作一个以点O为顶点的直角。
小梦的作法
2. 如图,已知一个点O,请用尺规作一个以点O为顶点的直角。 3. 如图,已知 , 点E在上,以E为顶点,为一边作 , 交于F;(请用尺规完成作图,保留作图痕迹,不必写作法)
3. 如图,已知 , 点E在上,以E为顶点,为一边作 , 交于F;(请用尺规完成作图,保留作图痕迹,不必写作法)
二、尺规作角的和与差
-
4. 如图所示,已知和 , 利用尺规作 .
 5. 已知 , , 用尺规完成下列作图:
5. 已知 , , 用尺规完成下列作图: (1)、求作;(2)、 .
(1)、求作;(2)、 .三、过直线外一点作这条直线的平行线
-
6. 下面四个图是小明用尺规过点C作AB边的平行线所留下的作图痕迹,其中正确的是( )A、
 B、
B、 C、
C、 D、
D、 7. (1)知识再现:图1,教材中,我们可以用直尺和三角尺,过直线外一点P画已知直线b的平行线a.下面是操作步骤:①沿直尺上移三角尺使三角尺一边经过点P;②用直尺紧靠三角尺的另一边;③沿三角尺的边作出直线a;④用三角尺的一边贴住直线b;正确的操作顺序是:_________________________(填序号);
7. (1)知识再现:图1,教材中,我们可以用直尺和三角尺,过直线外一点P画已知直线b的平行线a.下面是操作步骤:①沿直尺上移三角尺使三角尺一边经过点P;②用直尺紧靠三角尺的另一边;③沿三角尺的边作出直线a;④用三角尺的一边贴住直线b;正确的操作顺序是:_________________________(填序号);(2)类比迁移:图2中,利用直尺与圆规作图:作直线a,使a经过点P且 . (保留作图痕迹,不写画法)

四、尺规作三角形
-
8. 如图,已知线段a和 , 利用尺规作 , 使得 , , .
 9. 如图, 已知线段a, b, h(h<b), 用尺规作锐角三角形ABC, 使BC=a, AB=b, BC边上的高AD=h.
9. 如图, 已知线段a, b, h(h<b), 用尺规作锐角三角形ABC, 使BC=a, AB=b, BC边上的高AD=h.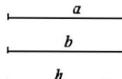 10. 如图,已知线段a和请用尺规完成下列作图:
10. 如图,已知线段a和请用尺规完成下列作图: (1)、作一个使(2)、作一个使
(1)、作一个使(2)、作一个使五、结合尺规作图的全等问题
-
11. 如图,用直尺和圆规作ΔABC和ΔDBC,则ΔABC≌ΔDBC,理由是( )
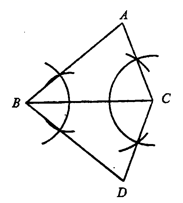 A、SAS B、ASA C、AAS D、SSS12. 【提出问题】
A、SAS B、ASA C、AAS D、SSS12. 【提出问题】在本学期的学习中,我们已经知道了三角形全等的判定方法和直角三角形全等的判定方法 , 数学兴趣小组组长小唐带领小组成员继续对“两边分别相等且其中一组等边的对角相等的两个三角形”的情形进行探究.
【探索研究】成员小凡根据三角形的分类提出以下探索路径:
已知:在和中, , , .
(1)如图①,当时,可知 , 判定全等的方法是____.

(2)如图②,当时,请用直尺和圆规作出 , 通过作图,可知与_________全等.(填“一定”或“不一定”)

(3)如图③,当时,与是否全等?若全等,请加以证明;若不全等,请举出反例.

【归纳总结】成员悦悦对以上探索进行总结:
(4)如果两个三角形的两边分别相等且其中一组等边的对角相等,那么当这组对角是_____时,这两个三角形一定全等.(填序号)
①锐角;②直角;③钝角.
【结论应用】智多星小崔根据以上探究结果,提出以下问题:
(5)如图④,为等边三角形( , ),是外角的平分线,点E在边上,点F在上,且 , 求的度数.

六、尺规作角平分线
-
13. 如图①,已知 ,用尺规作它的角平分线(如图②).

尺规作图具体步骤如下,
第1步:以 为圆心,以 为半径画弧,分别交射线 于点 ;
第2步:分别以 为圆心,以 为半径画弧,两弧在 内部交于点 ;
第3步:画射线 .射线 即为所求.
下列说法正确的是( )
A、 有最小限制, 无限制 B、 的长 C、 的长 D、连接 ,则 垂直平分14. 如图,在中, , 利用尺规在上分别截取;分别以点M,N为圆心,大于的长为半径作弧,两弧在内部交于点E,作射线交于点F,若 , 点H为线段上的一动点,则的最小值是 . 15. 作图并证明:如图,请用尺规在线段下方作一点P,使得平分角 , 且 . (保留作图痕迹,不写作法);连接 , 求证:平分 .
15. 作图并证明:如图,请用尺规在线段下方作一点P,使得平分角 , 且 . (保留作图痕迹,不写作法);连接 , 求证:平分 .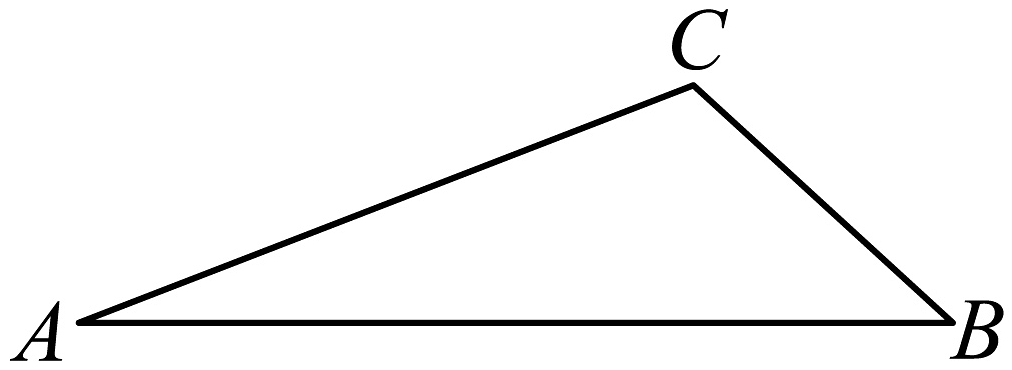 16. 如图,在 ABC中,∠C=90°,按下列要求用直尺和圆规作图.(不写作法,保留作图痕迹)
16. 如图,在 ABC中,∠C=90°,按下列要求用直尺和圆规作图.(不写作法,保留作图痕迹) (1)、如图①,在边BC上求作一点P,使点P到点C的距离等于点P到边AB的距离;(2)、如图②,在边AB上求作一点Q,使点Q到点A的距离等于点Q到边BC的距离.17. 已知△ABC(如图),用直尺和圆规作一点P,使它到三边的距离都相等(只要求作出图形,并保留作图痕迹)。
(1)、如图①,在边BC上求作一点P,使点P到点C的距离等于点P到边AB的距离;(2)、如图②,在边AB上求作一点Q,使点Q到点A的距离等于点Q到边BC的距离.17. 已知△ABC(如图),用直尺和圆规作一点P,使它到三边的距离都相等(只要求作出图形,并保留作图痕迹)。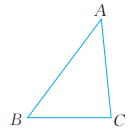
七、尺规作垂直平分线
-
18. 下列选项的尺规作图,能推出的是( )A、
 B、
B、
C、 D、
D、 19. 如图,一张纸上有A,B,C,D四个点,请用尺规找出一点M,使得
19. 如图,一张纸上有A,B,C,D四个点,请用尺规找出一点M,使得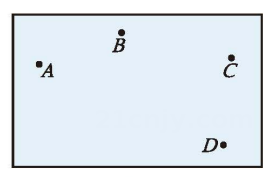 20. 已知线段a,h(图),用直尺和圆规作等腰三角形 , 使底边 , 底边边上的高线长为h.
20. 已知线段a,h(图),用直尺和圆规作等腰三角形 , 使底边 , 底边边上的高线长为h.


