相关试卷

1、古人言：“读书可以启智，读书可以明理，读书可以医愚.”某校计划购进x本某品牌图书，已知该品牌图书的售价为每本20元，经过协商，该品牌图书的销售商给出两种优惠方案：
方案一：所有该品牌图书都按原价的八折销售；
方案二：充值30元办理一张该品牌图书的专购优享卡，购买该品牌图书时，每本将在原价八折的基础上再降1元.

(1)、分别求方案一的实际付款金额 y₁（元）和方案二的实际付款金额 y₂（元）与购买数量x（本）之间的函数关系式；

(2)、请为该学校写出较为省钱的购买方案.

查看解析
2、某通信公司就手机流量套餐推出三种方案，如下表：

A方案
B方案
C方案
每月基本费用（元）
20
56
266
每月免费使用流量（兆）
1024
m
无限
超出后每兆收费（元）
n
n

A，B，C三种方案每月所需的费用y（元）与每月使用的流量x（兆）之间的函数关系如图所示.

(1)、请直接写出m，n的值；

(2)、在A方案中，当每月使用的流量不少于 1024兆时，求每月所需的费用y（元）与每月使用的流量x（兆）之间的函数关系式；

(3)、在这三种方案中，当每月使用的流量超过多少兆时，选择C方案最划算?

查看解析
3、小江和小北两人相约爬山锻炼身体，山顶距出发地600 米.小江爬到半山腰休息了5分钟，然后加速继续往上爬.小北因有事耽搁，出发晚了8分钟，为追赶小江，小北开始爬山的速度是小江休息前速度的2倍，但爬到半山腰体力不支，于是减速爬到山顶.两人距出发地的路程y（米）与小江的爬山时间x（分）之间的函数关系如图所示（注：小江、小北每一段的爬行均视为匀速）.

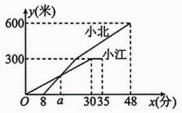(1)、小江休息前爬山的速度为米/分，小北减速后爬山的速度为米/分；

(2)、求a的值；

(3)、若小江不想晚于小北到达山顶，则他加速后的速度至少要比原来提高多少米/分?

查看解析
4、区间测速是指在某一路段前后设置两个监控点，根据车辆通过两个监控点的时间来计算车辆在该路段上的平均行驶速度.小春驾驶一辆小型汽车在高速公路上行驶，其间经过一段长度为 20 km的区间测速路段，从该路段起点开始，他先匀速行驶 $\frac{1}{12}$ h，再立即减速以另一速度匀速行驶（减速时间忽略不计），当他到达该路段终点时，测速装置测得该辆汽车在整个路段行驶的平均速度为 100 km/h.汽车在区间测速路段行驶的路程y（km）与在此路段行驶的时间x（h）之间的函数图象如图所示.

(1)、a的值为；

(2)、当 $\frac{1}{12} \leq x \leq a$ 时，求y与x 之间的函数关系式；

(3)、通过计算说明在此区间测速路段内，该辆汽车减速前是否超速.（此路段要求小型汽车行驶速度不得超过120 km/h）

查看解析
5、实践活动：最多可以将几个杯子放进橱柜?
周末，小洲同学在家整理杯子时，想把一些规格相同的杯子（如图①）尽可能多地叠放在一起（如图②），放入高为40 cm的橱柜，于是他开始了以下探究：
【测量数据】
小洲同学经过探究测量后，将按图②所示方式叠放杯子的总高度 H（cm）与杯子的个数n的数据情况记录如下表：
杯子的个数n
1
2
3
4
5
杯子的总高度 H（cm）
6.8
8.3
9.8
11.3
12.8
【建立模型】
根据表中所记录的数据，在图③的平面直角坐标系中描出对应点，依据你所学的知识选择合适的函数模型，求出 H 关于n的函数表达式.
【应用模型】
请根据你所探究出的规律，帮助小洲算算看，他最多可以将多少个杯子叠放在一起放入橱柜.

查看解析
6、如图，已知直线 $y_{1} = k x + b$ 过点A（0，3），且与直线. $y_{2} = m x$ 交于点 P（1，m），则关于x的不等式组 mx>kx+b> mx-3的解是.

查看解析
7、如图，若直线 $l_{1} : y = x + 1$ 与直线l₂：y= kx+b相交于点P（a，2），则关于x的不等式x+1> kx+b的解为.

查看解析
8、在同一平面直角坐标系中，一次函数y₁=ax+b与 $y_{2} = m x + n$ 的图象如图所示.

(1)、关于x，y的方程组 ${\begin{matrix} a x - y = - b, \\ m x - y = - n \end{matrix}$ 的解为；

(2)、当时， $y_{1} > y_{2} .$

查看解析
9、已知直线y= kx+b（k≠0）与直线y=3x+3关于y轴对称，则k= ， b=.

查看解析
10、如图，直线l₁ 过原点，直线 l₂的表达式为 $y = - \frac{\sqrt{3}}{3} x + 2,$ 且直线 l₁和l₂ 互相垂直，交点为 P，那么直线 l₁的函数表达式为（）

A、 $y = \frac{1}{3} x$ B、 $y = \frac{\sqrt{3}}{3} x$ C、 $y = \frac{\sqrt{3}}{2} x$ D、 $y = \sqrt{3} x$

查看解析
11、已知A（x₁ ， y₁），B（x₂ ， y₂）是一次函数y=2x-m图象上的两个点，请用“>”或“=”或“<”填空.

(1)、若 $x_{1} > x_{2},$ 则y₁y₂；

(2)、记 $W = \frac{y_{1} - y_{2}}{x_{1} - x_{2}},$ 则W0.

查看解析
12、如图，在同一平面直角坐标系中，一次函数. $y = k_{1} x + b_{1}$ 与 $y = k_{2} x + b_{2}$ （其中k₁k₂≠0，k₁ ， k₂ ， b₁ ， b₂ 为常数）的图象分别为直线 l₁ ， l₂.下列结论正确的是（）

A、 $b_{1} + b_{2} > 0$ B、 $b_{1} b_{2} > 0$ C、 $k_{1} + k_{2} < 0$ D、 $k_{1} k_{2} < 0$

查看解析
13、已知一次函数 y=2x-3 与y=kx（k是常数，k≠0）的图象的交点坐标是（2，1），则关于x，y的方程组 ${\begin{matrix} y = 2 x - 3, \\ y = k x \end{matrix}$ 的解是.

查看解析
14、一次函数y= kx-b（k≠0）的图象如图所示.

(1)、kx - b = 0 的解是；

(2)、kx—b>0 的解是， kx-b>-1的解是.

查看解析
15、根据下列条件，确定一次函数的表达式.

(1)、图象平行于直线y=2x-1，且过点（1，3）；

(2)、图象与直线 y=2x-1关于x轴对称；

(3)、直线y=2x+b与两坐标轴围成的三角形的面积是 4；

(4)、图象由直线 y=2x-1先向左平移1个单位，再向上平移3个单位得到.

查看解析
16、生物学研究表明，某种蛇在一定生长阶段，其体长 y（cm）是尾长x（cm）的一次函数，部分数据如下表所示，则y与x之间的关系式为（）
尾长x（cm）
6
8
10
体长y（cm）
45.5
60.5
75.5

A、y=7.5x+0.5 B、y=7.5x-0.5 C、y=15x D、y=15x+45.5

查看解析
17、已知一次函数y=2x-4.

(1)、当x=1时，y的值为，当0≤x≤2时，y 的取值范围是，当0≤y≤2时，x的取值范围是；

(2)、当y=0时，x的值为；

(3)、若点 A（-3，y₁），B（-1，y₂）在一次函数y=2x-4的图象上，则y₁ ， y₂的大小关系为

查看解析
18、关于一次函数y=-x+6，下列说法正确的是（）

A、图象经过点（2，1） B、y随x的增大而减小 C、图象不经过第二象限 D、图象向上平移1个单位后得到的图象的函数表达式为y=-x+5

查看解析
19、正比例函数 y=kx（k≠0）的图象如图所示，则k的值可能是（）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、-1 D、 $- \frac{1}{3}$

查看解析

20、

概念	一般地，函数y= kx+b（k，b都是常数，且k≠0）叫做一次函数. 当b=0时，一次函数y= kx+b就成为y=kx（k为常数，k≠0），叫做正比例函数
图象	k>0，b>0	k>0，b<0	k<0，b>0	k<0，b<0

	经过第一、二、三象限	经过第 ① 象限	经过第一、二、四象限	经过第 ②象限
性质	当k>0时，y随x的增大而③		当k<0时，y随x的增大而④
常用结论：（1）一次函数 y= kx+b（k≠0）的图象是一条直线，且经过点（0，⑤），（⑥ ， 0）；（2）直线 y= kx+b可由直线y= kx平移得到

查看解析

上一页 207 208 209 210 211 下一页跳转

	A方案	B方案	C方案
每月基本费用（元）	20	56	266
每月免费使用流量（兆）	1024	m	无限
超出后每兆收费（元）	n	n

杯子的个数n	1	2	3	4	5
杯子的总高度 H（cm）	6.8	8.3	9.8	11.3	12.8

尾长x（cm）	6	8	10
体长y（cm）	45.5	60.5	75.5