鲁教版（五四制）数学六年级上学期期中仿真模拟试卷一

试卷更新日期：2025-09-18 类型：期中考试

进入出卷网下载

一、选择题：本题共10小题，每小题3分，共30分。每小题只有一个选项符合题目要求.

1. 如图所示的几何体，下列说法正确的是（）

A、几何体是三棱锥 B、几何体的侧面是三角形 C、几何体的底面是三角形 D、几何体有6条侧棱

查看试题解析
2. 下列图形中，（　　）不是正方体的展开图．

A、 B、 C、 D、

查看试题解析
3. 一个正方体的表面展开图如图所示，六个面上各有一字，连起来是“祝福祖国万岁”，把它折成正方体后，与“万”相对的字是（）.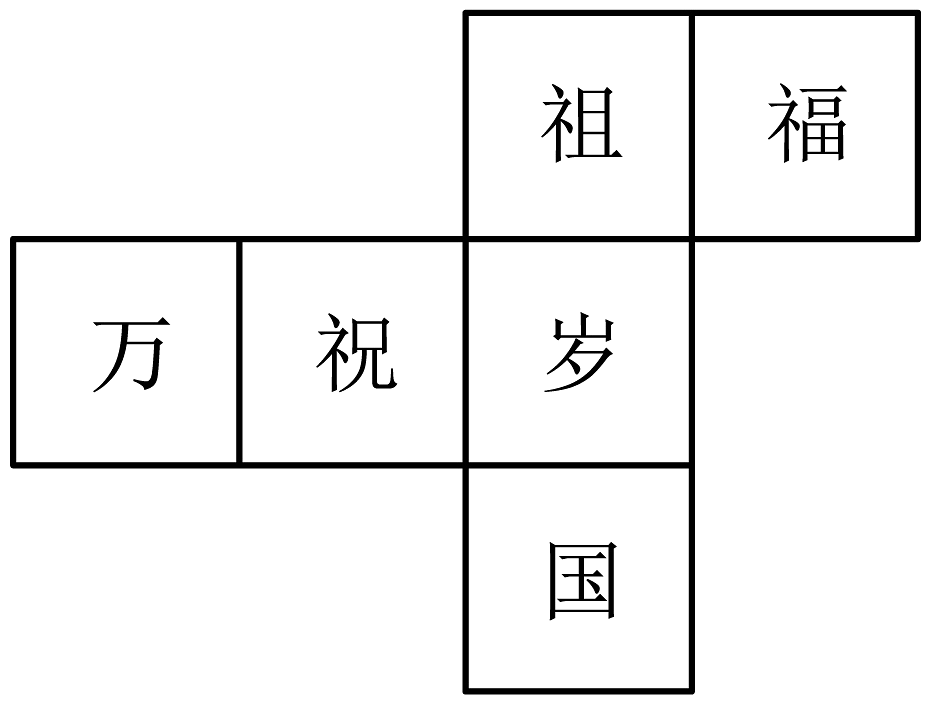

A、祖 B、国 C、岁 D、福

查看试题解析
4. 现有①②③④四种型号的铁皮，铁皮的形状与相关尺寸如图所示（单位：dm）．从中选两种，正好可以制成一个无盖圆柱形水桶（不计接头），则所选的这两种铁皮的型号是（）

A、①③ B、①④ C、②④ D、②③

查看试题解析
5. 下列关于近似数和精确度的说法不正确的是（）

A、3.2万精确到万位 B、0.0230精确到万分位 C、近似数1.6与1.60表示的意义不同 D、 $2.0 \times 10^{3}$ 精确到百位

查看试题解析
6. 在下列各数中： $- 10$ ， ${(- 4)}^{2}$ ， $+ (- 3)$ ， $- |- 2|$ ， ${(- 1)}^{2024}$ ， 0，其中是负数的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
7. $- 1.5$ 的倒数是（）

A、 $- \frac{3}{2}$ B、 $\frac{2}{3}$ C、 $- \frac{2}{3}$ D、 $\frac{3}{2}$

查看试题解析
8. 已知a+b＜0，ab＜0，|a|＞|b|，则（）．

A、a＞0，b＜0， B、a＜0，b＞0 C、a＞0，b＞0 D、a＜0，b＜0

查看试题解析
9. 分别用一平面去截如图所示的几何体，能得到截面是长方形的几何体有（）

A、①②③ B、①②④ C、①③④ D、①③⑤

查看试题解析
10. 用小立方块搭成的几何体，从正面和从上面看到的形状图如图所示，则搭成这样的几何体需要小立方块的块数为( )

A、最多需要8块，最少需要6块 B、最多需要9块，最少需要6块 C、最多需要8块，最少需要7块 D、最多需要9块，最少需要7块

查看试题解析

二、填空题：本题共5小题，每小题3分，共15分.

11. 折扇的每一根扇骨可以看作是一条线，当我们打开折扇时，众多扇骨同时运动，这些扇骨运动所形成的区域就构成了一个扇面，从数学的角度来解释，这种现象说明了．

查看试题解析
12. 如图所示是一个立体图形的展开图，请写出这个立体图形的名称：.

查看试题解析
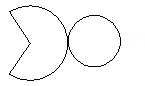13. 已知|a+1|+(b-2024)²=0，则a^b=.

查看试题解析
14. 如图所示，将一刻度尺放在数轴上.若刻度尺上0 cm和5 cm对应数轴上的点表示的数分别为-4和6，则刻度尺上7 cm对应数轴上的点表示的数是.

查看试题解析
15. 有一个正方体，六个面上分别写有数字 1 ， 2 ， 3 ， 4 ， 5 ， 6，如图是我们能看到的三种情况，如果记6的对面数字为a， 2的对面数字为b，那么 $a + b$ 的值为．

查看试题解析

三、解答题：本题共8小题，共75分.解答应写出文字说明、证明过程或演算步骤.

16. 计算：

(1)、(-6.5)-(-4 $\frac{1}{4}$ )+8 $\frac{3}{4}$ -(+3 $\frac{1}{2}$ )+5；

(2)、-1 $\frac{1}{2}$ ×(- $\frac{6}{7}$ )-(-5)÷(- $\frac{7}{6}$ )；

(3)、-1-48×( $\frac{5}{24}$ - $\frac{3}{16}$ + $\frac{1}{6}$ )；

(4)、-2²- $[(- 3) \times (- \frac{4}{3}) -(- 2)^{3}]$ .

查看试题解析
17. 阅读下面的解题过程：
计算 $: (- 5 \frac{5}{6}) + (- 9 \frac{2}{3}) + 17 \frac{3}{4} + (- 3 \frac{1}{2}) .$
解：原式 $= [(- 5) + (- \frac{5}{6})] + [(- 9) + (- \frac{2}{3})] +$ $[(+ 17) + (+ \frac{3}{4})] + [(- 3) + (- \frac{1}{2})]$
=[(-5)+( - 9) + (+ 17) + ( - 3)] + $[(- \frac{5}{6}) + + (- \frac{2}{3}) + (+ \frac{3}{4}) + (- \frac{1}{2})]$
= $0 + (- 1 \frac{1}{4}) = - 1 \frac{1}{4} .$
上面这种解题方法叫拆项法.
仿照上述解题过程计算： $(- 2024 \frac{5}{6}) +$ $(- 2025 \frac{2}{3}) + 4052 + (- 1 \frac{1}{2}) .$

查看试题解析
18. 在学习一个数的绝对值过程中，化简 $|a|$ 时，可以这样分类：当 $a > 0$ 时， $|a| = a$ ；当， $a = 0$ 时， $|a| = 0$ ；当 $a < 0$ 时， $|a| = - a$ ，请用这种方法解决下列问题：

(1)、当 $a = 3$ 时， $\frac{a}{|a|} =$ ______，当 $a = - 2$ 时， $\frac{a}{|a|} =$ ______．

(2)、已知a，b是有理数，当 $a < 0$ ， $b > 0$ 时，求 $\frac{a}{|a|} + \frac{b}{|b|}$ 的值．

(3)、已知 $|a| = 4, |b| = 7$ ，且 $a < b$ ，求 $a + b$ 的值．

查看试题解析
19. 将下列几何体进行分类：(在横线上写明序号即可)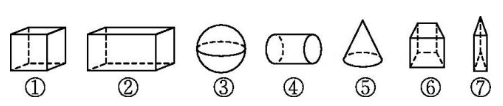

(1)、有顶点的几何体有；

(2)、截面可能为四边形的有；

(3)、能由平面旋转形成的有；

(4)、截面不可能是圆的有.

查看试题解析
20. 如图，是由几个大小相同的小正方体所搭成的几何体从上面看到的形状图，小正方形中的数字表示在这个位置小正方体的个数．

(1)、请画出从正面、左面看到的这个几何体的形状图；

(2)、若每个小正方体棱长为1cm ，请直接写出该几何体的表面积（包含底面）为．

查看试题解析
21. 如图所示的数轴中，点A 表示1，点 B 表示-2，试回答下列问题.

(1)、A，B 两点之间的距离是.

(2)、观察数轴，与点 A 的距离为 5 的点表示的数是.

(3)、若将数轴折叠，使点 A 与表示-3的点重合，则点 B 与表示数的点重合.

(4)、若数轴上M，N 两点之间的距离为2024(点 M在点 N的左侧)，且M，N 两点经过(3)中折叠后互相重合，则M，N 两点表示的数分别是和.

查看试题解析

22. 根据以下素材，探索完成任务．

实验探究：钢球在“磁悬浮”轨道上如何运动？
素材1	我国上海的“磁悬浮”列车，依靠“磁悬浮”技术使列车悬浮在轨道上行驶，从而减小阻力，因此列车时速可超过400公里．可利用钢球在“磁悬浮”轨道架上的运动模拟“磁悬浮”列车在轨道行驶，实验中钢球大小不计，假设钢球的运动都是匀速的．
素材2	现有一个长为 $180 cm$ 的“磁悬浮”轨道架，如图所示，轨道架上安置了三个大小、质量完全相同的钢球 $A$ 、 $B$ 、 $C$ ，左右各有一个钢制挡板 $D$ 和 $E$ ，其中 $C$ 到左挡板的距离为 $50 cm$ ， $B$ 到右挡板的距离为 $30 cm$ ， $A$ 、 $B$ 两球相距 $40 cm$ ．
素材3	在钢球碰撞实验中（相撞时间不计），当一钢球以一速度撞向另一静止钢球时，这个钢球停留在被撞钢球的位置，被撞钢球则以同样的速度向前运动，钢球接到左右挡板则以相同的速度反向运动．
问题解决
任务1	根据素材2，若 $A$ 球在数轴上表示坐标原点， $B$ 球表示的数为40，则 $C$ 球表示的数为_______，右挡板 $E$ 表示的数为_______．
任务2	碰撞实验中，若 $A$ 球以每秒 $10 cm$ 的速度向右匀速运动，从原点开始计时，请分别求出 $B$ 球第一次和第二次撞向右挡板 $E$ 的时间．
任务3	在任务1、2的条件下，当3个钢球运动的路程和为 $650 cm$ 时， $C$ 球在数轴上表示的数是_______．（直接写出答案）

查看试题解析

23. 欧拉（ $E u l e r$ ， 1707年1783年）为世界著名的数学家、自然科学家，他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究，发现多面体的顶点数 $V (V e r t e x)$ 、棱数 $E (E d g e)$ 、面数 $F (F l a t s u r f a c e)$ 之间存在一定的数量关系，给出了著名的欧拉公式.

(1)、观察下列多面体，并把下表补充完整：
名称
三棱锥
三棱柱
正方体
正八面体
图形
顶点数 $V$
4
棱数 $E$
6
面数 $F$
4

(2)、分析表中的数据，请写出 $V$ 、 $E$ 、 $F$ 之间的等量关系为：；一个多面体的面数比顶点数小8，且有30条棱，则这多面体的顶点数是；

(3)、某个玻璃饰品的外形是简单多面体，它的外表是由三角形和八边形两种多边形拼接而成，且有48个顶点，每个顶点处都有3条棱.请问该多面体表面三角形与八边形的个数之和是多少？

查看试题解析

名称	三棱锥	三棱柱	正方体	正八面体
图形
顶点数 $V$	4
棱数 $E$	6
面数 $F$	4