浙江省九年级上学期数学期中仿真模拟试题（一）

试卷更新日期：2025-09-17 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题, 每小题3分, 共30分,）

1. 下列计算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 ${(- a^{2})}^{3} = a^{6}$ C、 ${(- 2 a^{2})}^{3} = - 8 a^{6}$ D、 $2 a^{2} \div a^{2} = 2 a$

查看试题解析
2. 下列事件中，属于必然事件的是( )

A、任意画一个三角形，其内角和为180° B、打开电视机，正在播放广告 C、在一个没有红球的盒子里，摸到红球 D、抛一枚硬币，正面向上

查看试题解析
3. 如图，在▱ABCD中， $∠ A + ∠ C = 11 0^{°}$ ，则 $∠ A$ 的度数为（）

A、 $4 5^{°}$ B、 $5 5^{°}$ C、 $6 5^{°}$ D、 $7 0^{°}$

查看试题解析
4. 如图，以点O为位似中心的△ABC与△DEF的周长比为2：3，则OA：AD的值是（）

A、4：9 B、3：1 C、2：1 D、2：3

查看试题解析
5. 如图，在 $Rt △ A B C$ 中， $∠ B = 90 ° ， A B = 12 ， B C = 5$ ，则 $\tan A$ 的值为（）

A、 $\frac{12}{5}$ B、 $\frac{5}{12}$ C、 $\frac{5}{13}$ D、 $\frac{12}{13}$

查看试题解析
6. 若多项式 $2 x^{2} + k x - 24$ 因式分解后的结果是 $(a x + 3) (x - 8)$ ，则 $k$ 的值是（　　）

A、10 B、 $- 12$ C、 $- 13$ D、13

查看试题解析
7. 如图，在⊙O 中，已知直径AB⊥弦CD，∠BOD=70°，那么∠BAC的度数等于（）

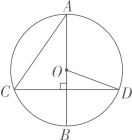A、55° B、45° C、35° D、25°

查看试题解析
8. 抛物线 $y = a x^{2} + 4 a x - 5$ 经过 $A (- 4, y_{1})$ ， $B (- 3, y_{2})$ ， $C (1, y_{3})$ 三点，且该抛物线与x轴的交点位于y轴两侧，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{2} < y_{1} < y_{3}$ B、 $y_{1} < y_{2} < y_{3}$ C、 $y_{3} < y_{1} < y_{2}$ D、 $y_{2} < y_{3} < y_{1}$

查看试题解析
9. 如图，在 $Rt △ A B C$ 中， $∠ A C B = 90 °, A C = 8, B C = 6$ ，点D是平面内的一动点，且 $A D = 3, M$ 为 $B D$ 的中点，在点D运动的过程中，线段 $C M$ 长度的取值范围是（）

A、 $\frac{3}{2} < C M \leq \frac{7}{2}$ B、 $\frac{7}{2} \leq C M \leq \frac{13}{2}$ C、 $6 \leq C M \leq 8$ D、 $\frac{3}{2} \leq C M < \frac{5}{2}$

查看试题解析
10. 如图，已知△ABC，O为AC上一点，以OB为半径的圆经过点A，且与BC，OC交于点D，E．设∠A=α，∠C=β（　　）

A、若α+β=70°，则 $\overset{⌢}{D E}$ 的度数为20° B、若α+β=70°，则 $\overset{⌢}{D E}$ 的度数为40° C、若α﹣β=70°，则 $\overset{⌢}{D E}$ 的度数为20° D、若α﹣β=70°，则 $\overset{⌢}{D E}$ 的度数为40°

查看试题解析

二、填空题（本大题共6小题, 每小题3分, 共18分）

11. 比较大小： $- 3$ $- 2$ ．（填“>”，“<”或“＝”）

查看试题解析
12. 一次函数y=(3m+1)x-2 的值随x的增大而增大，请写出一个满足条件的m的值：.

查看试题解析
13. 如图，已知A、B、C是⊙O上的三个点，∠ACB=110°，则∠AOB= ．

查看试题解析
14. 已知x₁ ， x₂ 是方程. $2 x^{2} - 3 x + 1 = 0$ 的两根，则代数式 $\frac{x_{1} + x_{2}}{1 + x_{1} x_{2}}$ 的值为.

查看试题解析
15. 如图，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 4$ ， $B C = 3$ ．将 $△ A B C$ 绕边 $B C$ 的中点P旋转，得到 $△ D E F$ ，边 $D E$ 恰好经过点C，过点A作 $A G ⊥ D E$ 于点G，则 $C G$ 的长为．

查看试题解析
16. 如图，点A的坐标为（0，4），以O点为圆心，以OA为半径的圆交x轴于点B，点C为第一象限圆上一动点，CD⊥x轴于D点，点I为△OCD的内心，则AI的最小值为.

查看试题解析

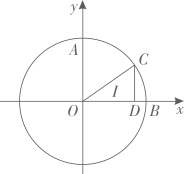
三、解答题（本大题共8个小题，共72分）

17. （1）计算： $\sqrt{2} \sin 45 ° + \tan 60 ° - 2 \cos 30 ° \tan 30 ° + {(π - 3)}^{0}$
（2）先化简再求值： $(1 - \frac{1}{x - 1}) \div \frac{x^{2} - 4}{x^{2} + 4 x + 4}$ ，其中 $x = {(\frac{1}{3})}^{- 1} + \tan 45 °$ ．

查看试题解析
18. 图1、图2均为4×5的正方形网格，每个小正方形的顶点称为格点，点A，B均在格点上，点P为线段AB上的一点．（仅用无刻度的直尺作图．）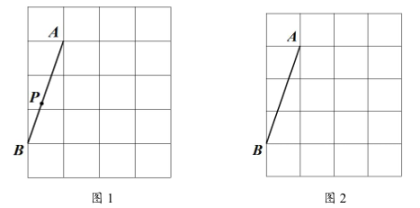

(1)、在图1中，画出一个以AB为边的正方形ABCD（保留作图痕迹）．

(2)、在（1）的基础上，在边CD上画点Q，使得PQ平分正方形ABCD的面积（保留作图痕迹）．

(3)、在图2中，画出一个以AB为边的非正方形的菱形ABEF（保留作图痕迹），连结此菱形各边中点所形成的四边形为 ▲ ．

查看试题解析
19. 如图，有一个可以自由转动的圆形转盘被平均分成3个扇形，分别标有1、2、3三个数字，小王和小李各转动一次转盘为一次游戏，当每次转盘停止后，指针所指扇形内的数为各自所得的数，一次游戏结束得到一组数（若指针指在分界线时重转）．

(1)、请你用树状图或列表的方法表示出每次游戏可能出现的所有结果：

(2)、两次转动转盘，第一次转得的数字记为 $m$ ，第二次记为 $n$ ， $A$ 点的坐标为 $(m, n)$ ，求 $A$ 点在函数 $y = x + 1$ 图象上的概率．

查看试题解析
20. 如图，在 $▱ A B C D$ 中， $A C = B C ， M ， N$ 分别是 $A B, C D$ 的中点．

(1)、求证：四边形 $A M C N$ 是矩形；

(2)、若 $\tan B = \sqrt{3} ， B C = 2$ ，求 $▱ A B C D$ 的面积．

查看试题解析
21. 如图1，装有水的水槽放置在水平桌面上，其横截面是以 $A B$ 为直径的半圆O， $A B = 52 cm, M N$ 为水面截线， $M N = 48 cm, G H$ 为桌面截线， $M N ∥ G H$ ．

(1)、作 $O C ⊥ M N$ 于点C，求 $O C$ 的长；

(2)、将图中的水倒出一部分得到图2，发现水面高度下降了 $14 cm$ ，求此时水面截线减少了多少．

查看试题解析
22. 杭州某地种植有机蔬菜，已知某种蔬菜的销售单价y（元）与销售月份x之间的关系满足 $y = - \frac{2}{3} x + 9$ ，每千克成本z（元）与销售月份x之间的关系如图所示，图象为抛物线，其最低点坐标是 $(6, 1)$ ．（其中x是满足 $1 \leq x \leq 12$ 的整数）

(1)、问：2月份每千克蔬菜成本是多少？

(2)、判断哪个月份销售每千克蔬菜的收益最大？并求最大收益．

查看试题解析
23. 新定义函数：在y关于x的函数中，若 $0 \leq x \leq 1$ 时，函数y有最大值和最小值，分别记 $y_{m a x}$ 和 $y_{m i n}$ ，且满足 $\{\begin{array}{l} y_{\min} > 0 \\ 2 y_{\min} > y_{\max} \end{array}$ ，则我们称函数y为“三角形函数”．

(1)、若函数 $y = x + a$ 为“三角形函数”，求a的取值范围；

(2)、判断函数 $y = x^{2} - \frac{\sqrt{2}}{2} x + 1$ 是否为“三角形函数”，并说明理由；

(3)、已知函数 $y = x^{2} - 2 m x + 1$ ，若对于 $0 \leq x \leq 1$ 上的任意三个实数a，b，c所对应的三个函数值都能构成一个三角形的三边长，则求满足条件的m的取值范围．

查看试题解析
24. 如图1，在 $△ A B C$ 中，以 $A B$ 为直径作 $⊙ O$ 交 $A C$ 于点 $E$ ，已知 $A B = 4$ ， $A E = C E$ ．

(1)、求证： $A B = B C$ ；

(2)、如图2，将点 $B$ 关于 $A C$ 作轴对称得到点 $D$ ，连结 $A D, C D$ ，得到四边形 $A B C D$ ，设 $A E = m$ ．四边形 $A B C D$ 的面积为 $n$ ．
①求 $n$ 关于 $m$ 的函数关系式：
②四边形 $A B C D$ 的面积 $n$ 是否有最大值，若有，请你求出 $n$ 的最大值．

查看试题解析