鲁教版（五四制）数学七年级上学期期中仿真模拟试卷二（范围：1.1-4.2）

试卷更新日期：2025-09-18 类型：期中考试

进入出卷网下载

一、选择题：本题共10小题，每小题3分，共30分。每小题只有一个选项符合题目要求.

1. 下列图标是节水、节能、低碳和绿色食品的标志，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 用直尺和圆规作线段的垂直平分线，下列作法正确的是（　　）

A、 B、 C、 D、

查看试题解析
3. 如图， $A C$ 与 $B D$ 交于点O，若 $O A = O D$ ，要用“SAS”证明 $△ A O B ≌ △ D O C$ ，还需要的条件是（）

A、 $O B = O C$ B、 $A B = D C$ C、 $∠ A = ∠ D$ D、 $∠ B = ∠ C$

查看试题解析
4. 如图，在三角形 $A B C$ 中， $∠ A = 80 °$ ， $B D$ 平分 $∠ A B C$ ， $C D$ 平分 $∠ A C B$ ，其角平分线相交于 $D$ ，则 $∠ B D C =$ （）

A、 $120 °$ B、 $135 °$ C、 $130 °$ D、 $125 °$

查看试题解析
5. 在0.7， $\sqrt[3]{5}$ ， $- \frac{24}{11}$ ， $\sqrt{9}$ ， $\frac{π}{3}$ ， 2.010010001六个实数中，无理数的个数有（）

A、5个 B、4个 C、3个 D、2个

查看试题解析
6. 如图，数轴上点 $C$ 所表示的数是（　　）

A、 $\sqrt{13}$ B、 $2 \sqrt{2}$ C、 $3.6$ D、 $3.7$

查看试题解析
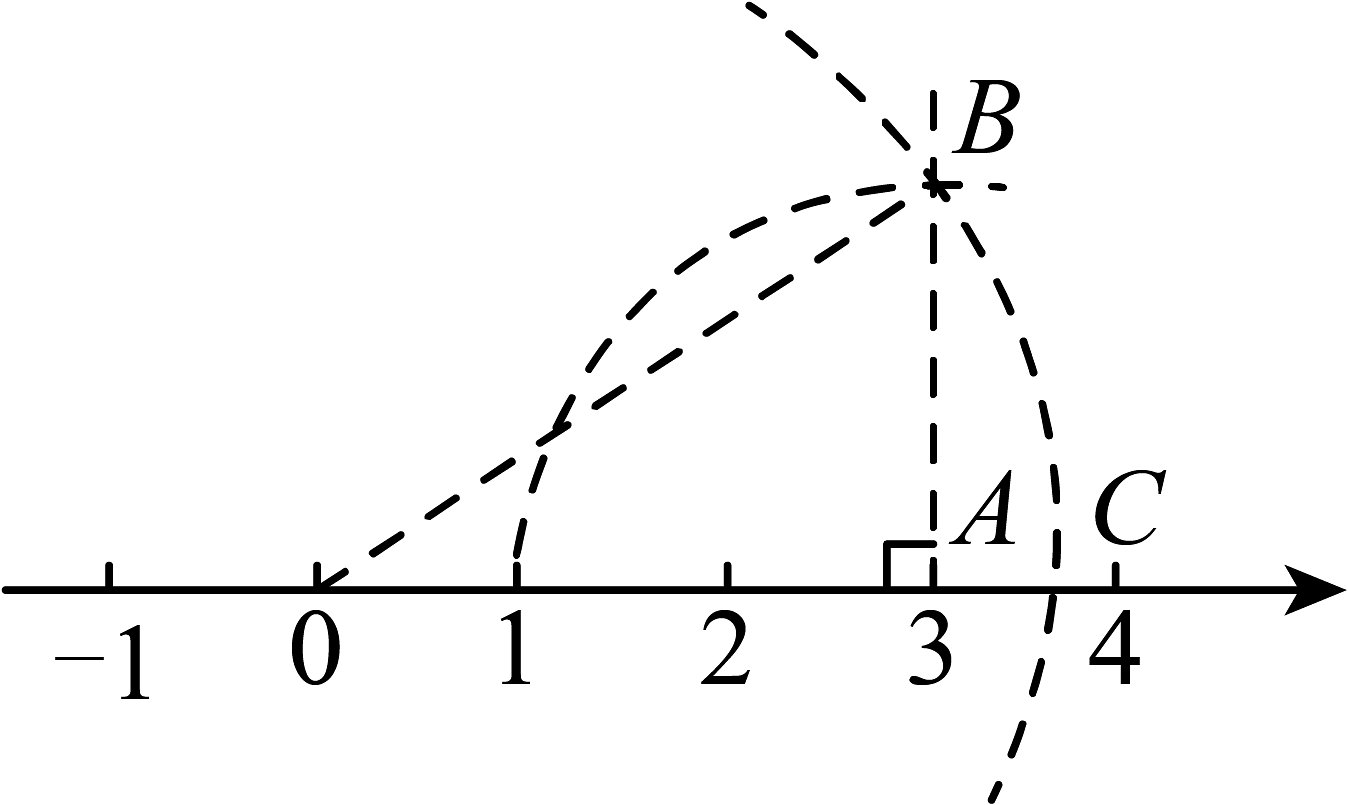7. 在我国古代数学著作《九章算术》中记载了一个有趣的问题，这个问题的意思是：如图，有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根新生的芦苇，它高出水面1尺．如果把这根芦苇沿与一边垂直的方向拉向岸边，那么它的顶端恰好到达岸边的水面，则水池的深度为（）

A、5尺 B、10尺 C、12尺 D、13尺

查看试题解析
8. 如图是 $4 \times 4$ 方格中的一个阴影正方形，若每个小方格的边长是1，则该阴影正方形的边长为（）．

A、 $\sqrt{12}$ B、 $\sqrt{9}$ C、 $\sqrt{8}$ D、 $\sqrt{10}$

查看试题解析
9. 一个正方形的面积是8，估计它的边长大小在（）

A、1与2之间 B、2与3之间 C、3与4之间 D、4与5之间

查看试题解析
10. 图1是第七届国际数学教育大会 $(I C M E - 7)$ 的会徽图案，它是由一串有公共顶点O的直角三角形(如图2所示)演化而成的．如果图2中 $O A_{1} = A_{1} A_{2} = A_{2} A_{3} = \dots = A_{7} A_{8} = 1$ ，那么 $O A_{8}$ 的长为( )

A、 $\sqrt{5}$ B、 $\sqrt{6}$ C、 $\sqrt{8}$ D、3

查看试题解析

二、填空题：本题共5小题，每小题3分，共15分.

11. 若整数 $a$ 满足条件 $\sqrt{5} < a < \sqrt{15}$ ，则 $a$ 的值是．

查看试题解析
12. 如图，在 $△ A B C$ 中， $∠ B = 35 °$ ，点 $D$ 是 $A B$ 的垂直平分线与 $B C$ 的交点，将 $△ A B D$ 沿着 $A D$ 翻折得到 $△ A E D$ ，则 $∠ C D E$ 的度数是．

查看试题解析
13. 如图所示的是某超市购物车的侧面简化示意图.测得支架AC=24cm，CB=18cm，两轮中心的距离AB=30cm，则点C到AB的距离为 cm.

查看试题解析
14. 已知 $\sqrt{a - 3} + \sqrt{b - 8} = 0$ ，则 ${(a - b)}^{2}$ 的平方根是．

查看试题解析
15. 如图，在Rt $△ A B C$ 中， $A C = 3, B C = 4, ∠ A C B = 9 0^{°}$ ，点P，Q分别是边AB和BC上的动点，始终保持 $A P = B Q$ ，连接AQ，CP，则 $A Q + C P$ 的最小值为.

查看试题解析

三、解答题：本题共8小题，共75分.

16. 将下列各实数按照分类将序号填入下面对应的横线上：
① $- \sqrt{10}$ ， ② $16$ ， ③ $- 4$ ， ④ $3.14$ ， ⑤ $0$ ， ⑥ $\frac{22}{7}$ ， ⑦ $\frac{π}{4}$ ．
整数：　　；
分数：　　；
负数：　　；
无理数：　　．

查看试题解析
17. 如图， $A D = B C$ ， $A C = B D$ ，求证： $∠ C = ∠ D$ ．

查看试题解析
18. 如图，在笔直的公路 $A B$ 旁有一座山，从山另一边的 $C$ 处到公路上的停靠站 $A$ 的距离为 $A C = 15 km$ ，与公路上另一停靠站 $B$ 的距离为 $B C = 20 km$ ，停靠站 $A$ 、 $B$ 之间的距离为 $A B = 25 km$ ，为方便运输货物现要从公路 $A B$ 上的 $D$ 处开凿隧道修通一条公路到 $C$ 处，且 $C D ⊥ A B$ ．

(1)、请判断 $△ A B C$ 的形状？

(2)、求修建的公路 $C D$ 的长．

查看试题解析
19. 如图所示， $A ， E ， B ， D$ 在同一直线上， $A B = D E$ ， $A C = D F$ ，要使 $△ A B C ≌ △ D E F$ ，需添加的一个条件是________，并说明理由．

查看试题解析
20. 如图1，正方形 $M N P Q$ 的面积为4，连结各边中点，得到一个新的正方形 $A B C D$ ．

(1)、求出图1中正方形 $A B C D$ 的面积及其边长；

(2)、如图2，把正方形 $A B C D$ 放到数轴上，使得边 $D A$ 与数轴重合，且点A落在数轴上表示 $- 1$ 的点处，现正方形 $A B C D$ 分别做以下运动：
①将正方形 $A B C D$ 绕点A顺时针旋转至边 $A B$ 与数轴重合，假设此时点B所表示的数为m；
②将正方形 $A B C D$ 沿数轴正方向移动2个单位，假设此时点A所表示的数为n．
试求m，n的值并比较m与n的大小．

查看试题解析
21. 如图，已知AD∥BC，点E是CD上一点，AE平分∠BAD，BF平分∠ABC，延长BE交AD的延长线于点F
（1）求证：△ABE≌△AFE；
（2）若AD＝2，BC＝6，求AB的长．

查看试题解析
22. 著名的赵爽弦图（如图①，其中四个直角三角形较大的直角边长都为 $a$ ，较小的直角边长都为 $b$ ，斜边长部为 $c$ ），大正方形的面积可以表示为 $c^{2}$ ，也可以表示为 $4 \times \frac{1}{2} a b + {(a - b)}^{2}$ ，由推导出重要的勾股定理：如果直角三角形两条直角边长为 $a$ ， $b$ ，斜边长为 $c$ ，则 $a^{2} + b^{2} = c^{2}$ ．

(1)、图②为美国第二十任总统伽菲尔德的“总统证法”，请你利用图②推导勾股定理：

(2)、如图③，在一条东西走向河流的一侧有一村庄 $C$ ，河边原有两个取水点 $A$ 、 $B$ ， $A B = A C$ ，由于某种原因，由 $C$ 到 $A$ 的路现在已经不通，该村为方便村民取水决定在河边新建一个取水点 $H$ （ $A$ 、 $H$ 、 $B$ 在同一条直线上），并新修一条路 $C H$ ，且 $C H ⊥ A B$ ．测得 $C H = 0.8$ 千米， $H B = 0.4$ 千米，求新路 $C H$ 比原路 $C A$ 少多少千米？

(3)、已知 $△ A B C$ 中， $A C = 10$ ， $B C = 17$ ， $A B = 21$ ，求 $△ A B C$ 的面积．

查看试题解析
23. 【探究与证明】
【新定义】顶角相等且顶角顶点重合的两个等腰三角形互为“兄弟三角形”.

(1)、如图1， $△ A B C$ 和 $△ A D E$ 互为“兄弟三角形”，点 $A$ 为重合的顶角顶点.则 $∠ B A D$ $∠ C A E$ （填“>”、“<”或“=”）；

(2)、如图2， $△ A B C$ 和 $△ A D E$ 互为“兄弟三角形”，点 $A$ 为重合的顶角顶点，连接 $B D$ 、 $C E$ ，试猜想线段 $B D$ 、 $C E$ 的大小关系，并证明你的结论；

(3)、如图3， $△ A B C$ 和 $△ A D E$ 互为“兄弟三角形”，点 $A$ 为重合的顶角顶点，点 $D$ 、点 $E$ 均在 $△ A B C$ 外，连接 $B D$ 、 $C E$ 交于点 $M$ ，连接 $A M$ ，求证： $M A$ 平分 $∠ B M E$ .

查看试题解析