鲁教版(五四制)数学七年级上学期期中仿真模拟试卷一(范围:1-3章)
试卷更新日期:2025-09-17 类型:期中考试
一、选择题:本题共10小题,每小题3分,共30分。每小题只有一个选项符合题目要求.
-
1. 如图所示,在△ABC和△DEF中,点A,E,B,D在同一条直线上,AC∥DF,AC=DF,只添加一个条件,不能判定△ABC≌△DEF的是( )
 A、AE=DB B、∠C=∠F C、BC=EF D、∠ABC=∠DEF2. 如图,AD是△ABC的中线,点E、F分别是射线AD上的两点,且DE=DF,则下列结论不正确的是( )
A、AE=DB B、∠C=∠F C、BC=EF D、∠ABC=∠DEF2. 如图,AD是△ABC的中线,点E、F分别是射线AD上的两点,且DE=DF,则下列结论不正确的是( ) A、△BDF≌△CDE B、△ABD和△ACD面积相等 C、BF∥CE D、AE=BF3. 如图,绕点顺时针旋转到的位置.如果 , 那么等于( )
A、△BDF≌△CDE B、△ABD和△ACD面积相等 C、BF∥CE D、AE=BF3. 如图,绕点顺时针旋转到的位置.如果 , 那么等于( ) A、 B、 C、 D、4. 如图,在中, , 以点为圆心,适当长为半径画弧分别交于点和点 , 再分别以点为圆心,大于的长为半径画弧,两弧交于点 , 连接并延长交于点 . 若的面积为8,则的面积是( )
A、 B、 C、 D、4. 如图,在中, , 以点为圆心,适当长为半径画弧分别交于点和点 , 再分别以点为圆心,大于的长为半径画弧,两弧交于点 , 连接并延长交于点 . 若的面积为8,则的面积是( ) A、8 B、16 C、12 D、245. 已知△ABC的三边长分别为5,13,12,则△ABC的面积为( )A、30 B、60 C、78 D、不能确定6. 如图,将△ABC放在正方形网格中(图中每个小正方形边长均为1),点A,B,C恰好在网格图中的格点上,那么∠ABC 的度数为 ( )
A、8 B、16 C、12 D、245. 已知△ABC的三边长分别为5,13,12,则△ABC的面积为( )A、30 B、60 C、78 D、不能确定6. 如图,将△ABC放在正方形网格中(图中每个小正方形边长均为1),点A,B,C恰好在网格图中的格点上,那么∠ABC 的度数为 ( ) A、90° B、60° C、45° D、30°7. 在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇沿与一边垂直的方向拉向岸边,那么它的顶端恰好到达岸边的水面,则水池的深度为( )
A、90° B、60° C、45° D、30°7. 在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇沿与一边垂直的方向拉向岸边,那么它的顶端恰好到达岸边的水面,则水池的深度为( ) A、5尺 B、10尺 C、12尺 D、13尺8. 如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )
A、5尺 B、10尺 C、12尺 D、13尺8. 如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( ) A、SAS B、ASA C、AAS D、SSS9. 在如图的正方形网格中,∠1+∠2+∠3=( )
A、SAS B、ASA C、AAS D、SSS9. 在如图的正方形网格中,∠1+∠2+∠3=( ) A、105° B、120° C、115° D、135°10. 如图,在△ABC中,∠ACB=60°,AG平分∠BAC交BC与点G , BD平分∠ABC交AC于点D , AG、BD相交于点F , BE⊥AG交AG的延长线于点E , 连接CE , 下列结论中正确的是( )
A、105° B、120° C、115° D、135°10. 如图,在△ABC中,∠ACB=60°,AG平分∠BAC交BC与点G , BD平分∠ABC交AC于点D , AG、BD相交于点F , BE⊥AG交AG的延长线于点E , 连接CE , 下列结论中正确的是( )
①若∠BAD=70°,则∠EBC=5°;②BF=2EF;③BE=CE;④AB=BG+AD .
A、4个 B、3个 C、2个 D、1个二、填空题:本题共5小题,每小题3分,共15分.
-
11. 如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC≌Rt△ABD.添加的条件是: . (写一个即可)
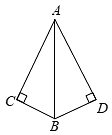 12. 如图,在中, , 平分 . 若 , , 则 .
12. 如图,在中, , 平分 . 若 , , 则 .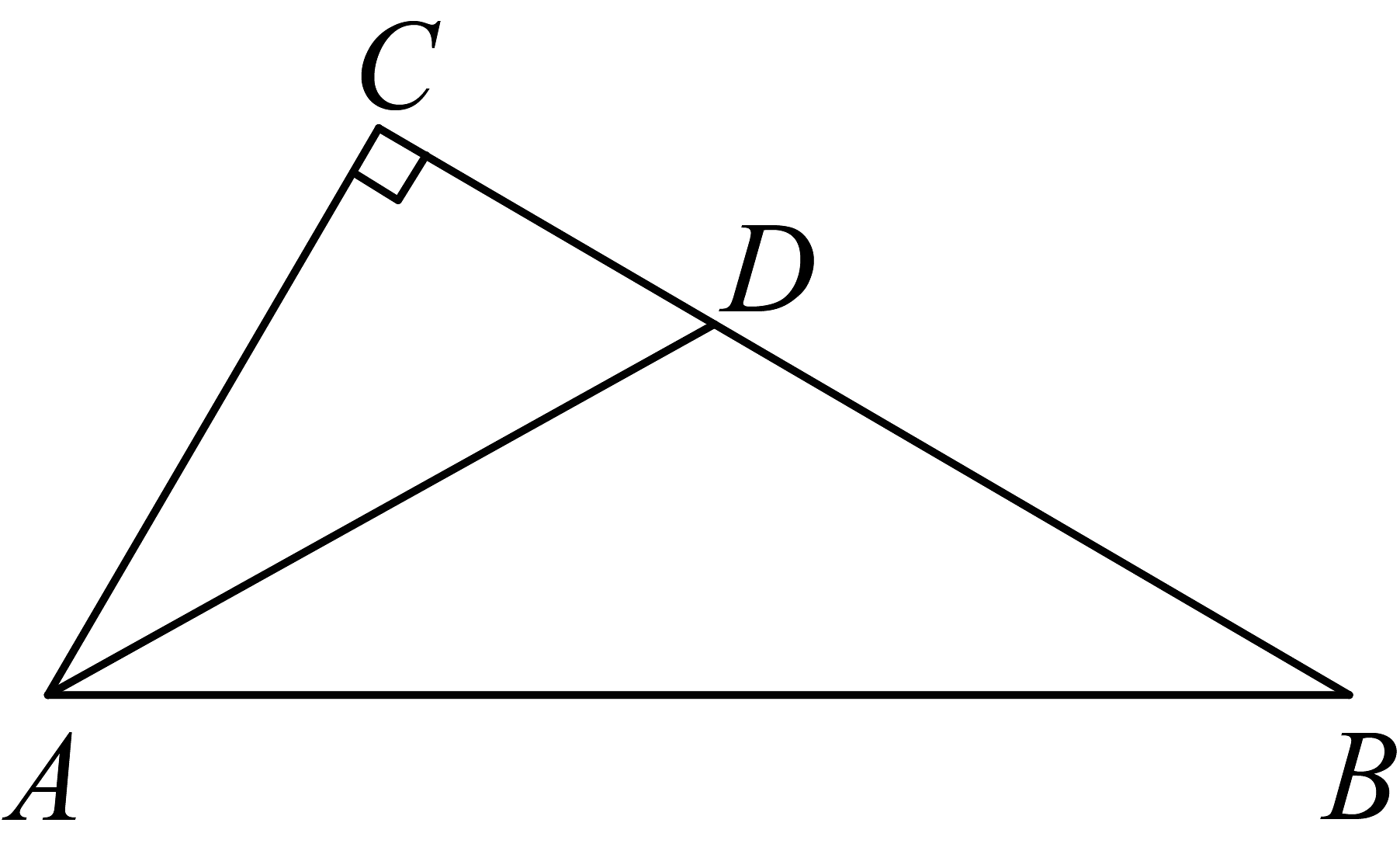 13. 如图,网格中每个小正方形的边长均为1,点在格点上,点在网格线上,线段的垂直平分线恰好经过格点 , 则的长是 .
13. 如图,网格中每个小正方形的边长均为1,点在格点上,点在网格线上,线段的垂直平分线恰好经过格点 , 则的长是 . 14. 在△ABC中,AB=AC,BC=10,AB的垂直平分线与AC的垂直平分线分别交BC于点D,E,且DE=4,则AD+AE的值为 .15. 小明在公园里荡秋千.如图,小明坐在秋千的起始位置A处,荡绳与地面垂直,荡至右侧最高位置为 , 荡至左侧最高位置为 . 已知起始位置A离地面垂直距离为 , 点B离地面垂直距离为 . 点B到的水平距离为 , . 则点C离地面的垂直距离为m.
14. 在△ABC中,AB=AC,BC=10,AB的垂直平分线与AC的垂直平分线分别交BC于点D,E,且DE=4,则AD+AE的值为 .15. 小明在公园里荡秋千.如图,小明坐在秋千的起始位置A处,荡绳与地面垂直,荡至右侧最高位置为 , 荡至左侧最高位置为 . 已知起始位置A离地面垂直距离为 , 点B离地面垂直距离为 . 点B到的水平距离为 , . 则点C离地面的垂直距离为m.
三、解答题:本题共8小题,共75分.解答应写出文字说明、证明过程或演算步骤.
-
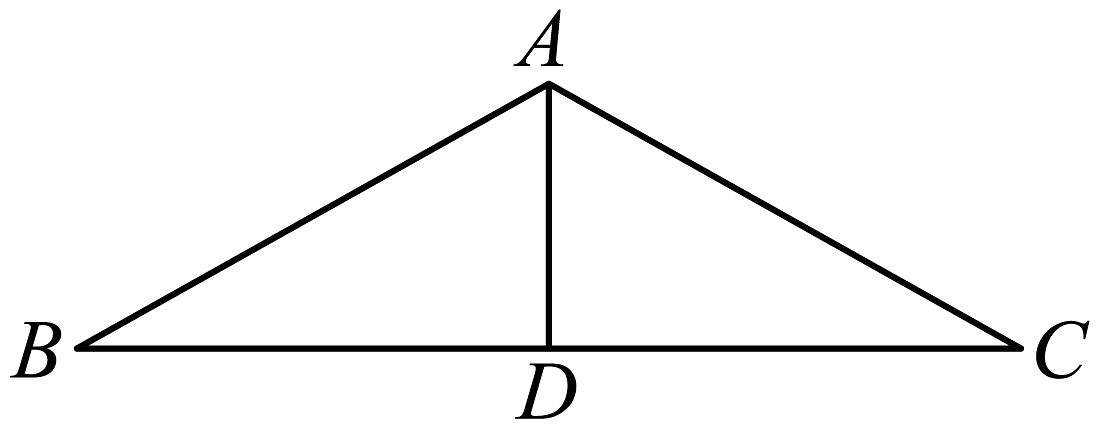
16. 如图,三角形钢架中, , AD是连接A与BC中点D的支架,
求证: .
 17. 如图,中,AC的垂直平分线分别交BC、AC于点E、F,且CE,作交BC于点.
17. 如图,中,AC的垂直平分线分别交BC、AC于点E、F,且CE,作交BC于点.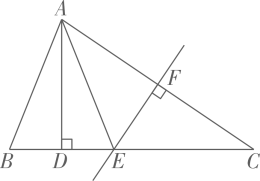 (1)、若 , 求的度数.(2)、若的周长为17cm,求DC的长.18. 如图,在一条紧的绳索一端系着一艘小船,河岸上一男孩拽着绳子另一端向右走,绳端从C移动到E,同时小船从A移动到 , 且绳长始终保持不变.回答下列问题:
(1)、若 , 求的度数.(2)、若的周长为17cm,求DC的长.18. 如图,在一条紧的绳索一端系着一艘小船,河岸上一男孩拽着绳子另一端向右走,绳端从C移动到E,同时小船从A移动到 , 且绳长始终保持不变.回答下列问题: (1)、根据题意可知:______(填“”、“”、“”).(2)、若 , 点B在直线AF上,米,米,米,求小男孩需向右移动的距离.(结果保留根号)19. 如图,在和中,在同一条直线上,已知: , 下列给出三个条件: . 解答下列问题:
(1)、根据题意可知:______(填“”、“”、“”).(2)、若 , 点B在直线AF上,米,米,米,求小男孩需向右移动的距离.(结果保留根号)19. 如图,在和中,在同一条直线上,已知: , 下列给出三个条件: . 解答下列问题: (1)、请选择两个合适的作为已知条件,余下一个作为结论,并给出证明过程:
(1)、请选择两个合适的作为已知条件,余下一个作为结论,并给出证明过程:我选择 作为已知条件, 作为结论(填写序号).
(2)、在(1)的条件下,若与相交于点 , 求 .20. 如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“梦想三角形”. (1)、如图,在中, , . 求证:是“梦想三角形”.(2)、在中, , . 若是“梦想三角形”,求的长.21. 如图,分别过点C、B作的边上的中线及其延长线的垂线,垂足分别为E、F.
(1)、如图,在中, , . 求证:是“梦想三角形”.(2)、在中, , . 若是“梦想三角形”,求的长.21. 如图,分别过点C、B作的边上的中线及其延长线的垂线,垂足分别为E、F. (1)、求证:;(2)、若的面积为6,的面积为2,求的面积.22. 如图,点E,A,D,B在同一条直线上, , , .
(1)、求证:;(2)、若的面积为6,的面积为2,求的面积.22. 如图,点E,A,D,B在同一条直线上, , , .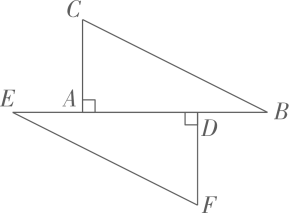 (1)、 与全等吗?请说明理由;(2)、 尺规作图:作的角平分线,与AC交于点P(不要求写作法,保留作图痕迹);(3)、 在条件(2)下,若 , , 求的面积.23. “一线三等角”模型是平面几何图形中的重要模型之一,“一线三等角”指的是图形中出现同一条直线上有3个角相等的情况,在学习过程中,我们发现“一线三等角”模型的出现,还经常会伴随着出现全等三角形.根据对材料的理解解决以下问题:
(1)、 与全等吗?请说明理由;(2)、 尺规作图:作的角平分线,与AC交于点P(不要求写作法,保留作图痕迹);(3)、 在条件(2)下,若 , , 求的面积.23. “一线三等角”模型是平面几何图形中的重要模型之一,“一线三等角”指的是图形中出现同一条直线上有3个角相等的情况,在学习过程中,我们发现“一线三等角”模型的出现,还经常会伴随着出现全等三角形.根据对材料的理解解决以下问题: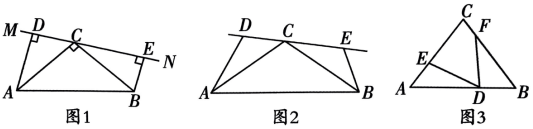 (1)、如图 1, 猜想DE,AD,BE之间的关系;(2)、如图2,将(1)中条件改为. 请问(1)中的结论是否成立?若成立,请给出证明;若不成立,请说明理由;(3)、如图3,在中,点D为AB上一点, , 请直接写出AB的长.
(1)、如图 1, 猜想DE,AD,BE之间的关系;(2)、如图2,将(1)中条件改为. 请问(1)中的结论是否成立?若成立,请给出证明;若不成立,请说明理由;(3)、如图3,在中,点D为AB上一点, , 请直接写出AB的长.