相关试卷
- 3.2整式的加减提升课时卷-北师大版数学七年级上册
- 鲁教版(五四制)数学六年级上学期期中仿真模拟试卷一
- 3.2 整式的加减基础课时卷-北师大版数学七年级上册
- 鲁教版(五四制)数学七年级上学期期中仿真模拟试卷二(范围:1.1-4.2)
- 2.1《 事件的可能性》(2)—浙教版数学九年级上册课堂分层训练
- 浙教版数学八年级上册4.3.2 坐标平面内图形的轴对称和平移 同步分层练习
- 浙教版 数学八年级上册4.3.1 坐标平面内图形的轴对称和平移 同步分层练习
- 浙教版数学八年级上册4.2 用方向和距离确定物体的位置 同步分层练习
- 浙江省九年级上学期数学期中仿真模拟试题(一)
- 鲁教版(五四制)数学七年级上学期期中仿真模拟试卷一(范围:1-3章)
-
1、 若点P(a,2025)在第二象限,则a的值可以是 ( )A、-2 B、0 C、1 D、2
-
2、两点间的距离
若P1(x1 , y1),P2(x2 , y2),则
(1)、当P1P2平行于x轴时,(2)、当P1P2平行于y轴时, -
3、点到坐标轴 (或原点)的距离
点P(x,y)到x轴的距离是 , 到y轴的距离是 , 到原点的距离是.
-
4、点的坐标特征
点的坐标
第一象限
第二象限
第三象限
第四象限
在x轴上
在y轴上
P(x,y)
(+,+)
(① )
(② )
(③ )
④=0
⑤=0
-
5、我们规定:若一个正整数 A 能写成 其中m与n都是两位数,且m与n的十位数字相同,个位数字之和为8,则称A为“方减数”,把A分解成 的过程,称为“方减分解”.例如:因为 25 与23的十位数字相同,个位数字5 与 3 的和为8,所以 602 是“方减数”,602 分解成602= 的过程就是“方减分解”.按照这个规定,最小的“方减数”是.
-
6、定义新运算“⊗”,规定:a⊗b= , 则(-2)⊗(-1)的运算结果为( )A、-5 B、-3 C、5 D、3
-
7、已知a1 为实数,规定运算: 按上述方法计算:当 时,a2024的值等于 ( )A、 B、 C、 D、
-
8、计算:(1)、20240+(2)、(π-6.8)0.
-
9、已知数轴上的点 A,B分别表示数a,b,其中-1<a<0,0<b<1.若 ab=c,数c在数轴上用点 C表示,则点 A,B,C在数轴上的位置可能是图中的 ( )A、
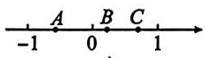 B、
B、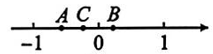 C、
C、 D、
D、
-
10、如图,数轴上三个不同的点A,B,P分别表示实数a,b,a+b,则下列关于数轴原点位置的描述正确的是 ( )
 A、原点在点A 的左侧 B、原点在A,B两点之间 C、原点在B,P两点之间 D、原点在点P 的右侧
A、原点在点A 的左侧 B、原点在A,B两点之间 C、原点在B,P两点之间 D、原点在点P 的右侧 -
11、如图1-4,数轴上位于数字1和2之间的点A表示的数为x+2,则x的取值范围是( )
 A、-2<x<-1 B、-1<x<0 C、0<x<1 D、1<x<2
A、-2<x<-1 B、-1<x<0 C、0<x<1 D、1<x<2 -
12、 计算:(1)、(2)、(3)、
-
13、 计算: ;;;
-
14、实数的运算
实数的运算
乘方
= , 其中a叫做 , n叫做
特别地
幂
(a≠0)
a-p=(a≠0,p是正整数),特别地:
实数的运算顺序
先算乘方和开方,再算乘除,最后算加减;若有括号,则先进行括号里的运算;同级运算,按照从左到右的顺序进行
-
15、 比较大小: (选填“>”“=”或“<”).
-
16、以下四个城市中某天中午 12时气温最低的是( )
北京
济南
太原
郑州
0 ℃
-1℃
-2℃
3 ℃
A、北京 B、济南 C、太原 D、郑州 -
17、实数a,b,c,d在数轴上的对应点的位置如图,则最小的实数为 ( )
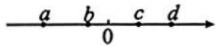 A、a B、b C、c D、d
A、a B、b C、c D、d -
18、实数的大小比较
数轴法
在数轴上表示的两个实数,右边的数总比左边的数 , 距离数轴原点越远的点表示的数,绝对值越
性质法
正数>0>负数;两个负数比较大小,绝对值大的数反而小
作差法
①a-b>0⇔;②a-b<0⇔;③a-b=0⇔
平方法
(常应用在无理数估值及含有无理数的大小比较中)
作商法
若a>0,b>0,则
②=1⇔a=b;
倒数法
若 ab>0,贝则 < ⇔a b
特殊值法
给字母取符合要求的数值,再代入验证比较大小
-
19、有下列说法:
①近似数3.50 是精确到个位的数;
②近似数 1.7 和1.70是一样的;
③近似数 1.05万是精确到百位的数;
④近似数 35.0是精确到十分位的数.
其中正确的是(填序号).
-
20、我国近年来大力推进国家教育数字化战略行动,截至 2024 年 6 月上旬,上线慕 课 数 量 超 过 7.8万 门,学习 人 次 达1290000000,建设和应用规模居世界第一.用科学记数法将数据1290000000 表示为( )A、1.29×108 B、12.9×108 C、1.29×109 D、129×107