-
1、
点与圆
设圆的半径是r，点到圆心的距离是d
点在圆外⇔①
点在圆上⇔②
点在圆内⇔③.
直线与圆
设⊙O的半径为 r，圆心 O到直线l的距离为d
直线l与⊙O 相交⇔④
直线 l与⊙O 相切⇔d=r
直线l与⊙O相离⇔⑤
-
2、如图，O为半圆的圆心，C，D为半圆上的两点，且 连结 AC 并延长，与BD 的延长线相交于点E.
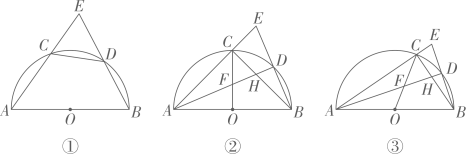(1)、求证：CD=ED.(2)、AD与OC，BC分别交于点F，H.①若 CF=CH，如图②，求证：CF·AF=FO·AH；
②若半圆的半径为2，BD=1，如图③，求 AC的长.
-
3、如图，在△ABC中，AB= D 为 AB 的中点，∠BAC=∠BCD， ⊙O：是△ACD的外接圆.
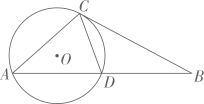(1)、求 BC的长；(2)、求⊙O的半径. -
4、 如图，在半径为3 的⊙O 中，直径 AB 与弦 CD相交于点 E，连结 AC，BD.若AC=2，则 cos D的值是（ ）
A、3 B、 C、 D、 -
5、如图，⊙O的弦AC=BD，且AC⊥BD于点E，连结AD.若 则⊙O的半径为（ ）
A、 B、2 C、3 D、3 -
6、 如图，⊙O的圆心O与正方形的中心重合，已知⊙O的半径和正方形的边长都为4，则圆上任意一点到正方形边上任意一点距离的最小值为 （ ）
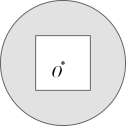A、 B、2 C、 D、 -
7、 某项目化研究小组只用一张矩形纸条和刻度尺来测量一次性纸杯杯底的直径.小敏同学想到了如下方法：如图，将纸条拉直并紧贴杯底，纸条的上下边沿分别与杯底相交于A，B，C，D四点，然后利用刻度尺量得该纸条的宽为3.5cm ，AB=3c m，CD=4 cm.请你帮忙计算纸杯杯底的直径为.
-
8、 如图，水暖管横截面是圆，半径r=5mm的水暖管有积水（阴影部分），水面的宽度AB 为8 mm，则积水的最大深度 CD（CD<r）是mm.
-
9、如图，AB是⊙O的直径，弦CD⊥OA 于点 E，连结OC，OD.若⊙O的半径为m，∠AOD=α，则下列结论一定成立的是 （ ）
A、OE=m·tanα B、CD=2m·sinα C、AE=m·cosα D、 -
10、 如图3，四边形 ABCD是⊙O的内接四边形，BE是⊙O的直径，连结 CE，DE.若∠BAD=110°，则∠DCE=°.
-
11、 如图，AB 是半圆O的直径，∠BAC=30°，则∠D 的度数是（ ）
A、130° B、125° C、120° D、115° -
12、
性质
圆内接四边形的对角
圆内接四边形的任意一个外角等于它的内对角
-
13、如图，点 A，B，C 在⊙O上，C 为. 的 中 点.若∠BAC = 2 ∠OAB， 则∠AOB等于（ ）
A、144° B、135° C、130° D、120° -
14、 如图，在⊙O中，△AOB 是 正 三 角形，点 C 在 上.若∠CAB=20°，则∠ABC=（ ）
A、10° B、15° C、20° D、25° -
15、
定义
顶 点 在 ， 并且 两 边 都 和 圆的角叫做圆周角
圆周角定理
圆周角的度数等于它所对弧上的圆心角度数的一半
圆周角定理的推论
半圆（或直径）所对的圆周角是；90°的圆周角所对的弦是
在同圆或等圆中，同弧或等弧所对的圆周角；相等的圆周角所对的弧也
防错提醒
圆的一条弧（弦）只对着一个圆心角，所对的圆周角有无数个；一条弧所对的圆周角的度数只有一个，而一条弦所对的圆周角的度数有两个，这两个度数的和为180°
-
16、 如图，AB，AC 是⊙O 的两条弦，OD⊥AB 于点D，OE⊥AC 于点E，连结OB，OC.若∠DOE=140°，则∠BOC的度数为 （ ）
A、70° B、80° C、90° D、100° -
17、 如图，AB是⊙O的直径， ∠COD=35°，则∠AOE的度数为 .
-
18、 如图，AB 是半圆O的直径，弦CD∥AB，CD=8，弦CD与直径AB 之间的距离为3，则AB=.
-
19、 如图，在⊙O中，点 C 在弦AB 上，连结OB，OC.若OB=5，AC=1，BC=5，则线段OC的长为.
-
20、如图，⊙O的直径CD垂直弦AB于点E，且CE=3，DE=7，则AE=（ ）
A、4 B、2 C、 D、