相关试卷
- 湘教版数学七年级上册3.4一元一次方程的应用 第二课时 同步分层练习
- 湘教版数学七年级上册3.4 一元一次方程的应用 第一课时 同步分层练习
- 浙教版数学八年级上册4.1.2 平面直角坐标系 同步分层练习
- 浙教版数学八年级上册4.1.1 平面直角坐标系 同步分层练习
- 浙教版数学八年级上册第3章 一元一次不等式 单元检测提升卷
- 浙教版数学八年级上册第3章 一元一次不等式 单元检测培优卷
- 浙教版数学八年级上册第3章 一元一次不等式 单元检测基础卷
- 北师大版数学八年级上册单元分层检测卷第二章 《实数》B卷
- 浙教版数学八年级上册3.5 一元一次不等式组 同步分层练习
- 湘教版数学七年级上册 3.3 一元一次方程的解法 第二课时 同步分层练习
-
1、 一个几何体是由若干个相同的正方体组成的,其主视图和左视图如图所示,则这个几何体最多可由多少个这样的正方体组成?( )
 A、12个 B、13个 C、14个 D、18个
A、12个 B、13个 C、14个 D、18个 -
2、 如图,用一个平面去截长方体,则截面形状为( )
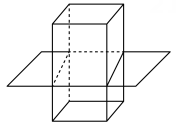 A、
A、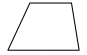 B、
B、 C、
C、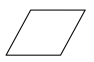 D、
D、
-
3、如图(1)是一个小正方体的侧面展开图,小正方体从图(2)所示的位置依次翻到第1格、第2格、第3格,这时小正方体朝上一面的字是( )
 A、奥 B、运 C、圣 D、火
A、奥 B、运 C、圣 D、火 -
4、如图是一个正四面体,它的四个面都是正三角形,现沿它的三条棱AC、BC、CD剪开展成平面图形,则所得的展开图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
5、下列物体的形状类似于球体的是( )A、茶杯 B、羽毛球 C、乒乓球 D、白炽灯泡
-
6、我们知道,将一个正方体或长方体的表面沿某些棱剪开,可以展成一个平面图形.
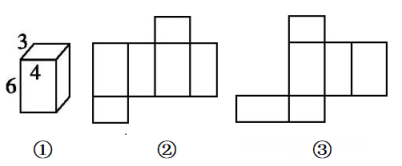 (1)、下列图形中,是正方体的表面展开图的是( )A、
(1)、下列图形中,是正方体的表面展开图的是( )A、 B、
B、 C、
C、 D、
D、 (2)、如图①所示的长方体,长、宽、高分别为4,3,6.若将它的表面沿某些棱剪开,展成一个平面图形,则下列图形中,是该长方体表面展开图的是( )A、
(2)、如图①所示的长方体,长、宽、高分别为4,3,6.若将它的表面沿某些棱剪开,展成一个平面图形,则下列图形中,是该长方体表面展开图的是( )A、 B、
B、 C、
C、 D、
D、 (3)、图②③分别是图①的一种表面展开图,已知图②的周长为52,请求图③的周长.(4)、图①的表面展开图还有不少,聪明的你能画出一个使周长最大的表面展开图吗?请画出这个表面展开图,并求出它的周长.
(3)、图②③分别是图①的一种表面展开图,已知图②的周长为52,请求图③的周长.(4)、图①的表面展开图还有不少,聪明的你能画出一个使周长最大的表面展开图吗?请画出这个表面展开图,并求出它的周长. -
7、(1)、根据图示规律填表:

图形编号
1×1的
正方形个数
2×2的
正方形个数
3×3的
正方形个数
4×4的
正方形个数
①
②
③
④
(2)、猜想:第n个图形共有多少个正方形? -
8、一个物体是由棱长为3 cm的正方体模型堆砌而成的,其从不同方向看到的形状图如图所示.
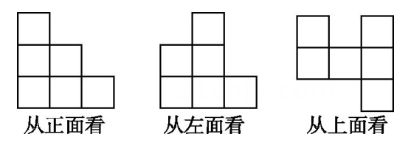 (1)、请在从上面看到的形状图上标出每个位置小正方体的个数;(2)、求该几何体的体积;(3)、求该几何体的表面积.
(1)、请在从上面看到的形状图上标出每个位置小正方体的个数;(2)、求该几何体的体积;(3)、求该几何体的表面积. -
9、一个几何体由若干个大小相同的小立方块搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请画出从正面和从左面看到的这个几何体的形状图.


-
10、将下列几何体进行分类:(在横线上写明序号即可)
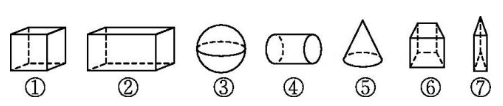 (1)、有顶点的几何体有;(2)、截面可能为四边形的有;(3)、能由平面旋转形成的有;(4)、截面不可能是圆的有.
(1)、有顶点的几何体有;(2)、截面可能为四边形的有;(3)、能由平面旋转形成的有;(4)、截面不可能是圆的有. -
11、四个长都是4 cm,宽都是3 cm,高都是2 cm的长方体,如果拼接在一起组成一个新的长方体,那么新长方体表面积的最大值为cm2.

-
12、如图所示是由10个大小相同的小立方块搭成的几何体,在保持从正面看和从左面看得到的平面图形不变的情况下,最多可以拿掉个小立方块.

-
13、如图所示,长方形ABCD的长AB=4,宽BC=3,以AB所在直线为轴,将长方形旋转一周后所得几何体从正面看到的图形的面积是.
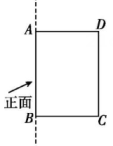
-
14、在墙角用若干个棱长为1 cm的小正方体摆成如图所示的几何体,则此几何体的体积为cm3.

-
15、一个正方体的六个面上分别写有数字1,2,3,4,5,6,三名同学从不同的角度观察的结果如图所示.若记2的对面为数字m,6的对面为数字n,则2m-n的值为.
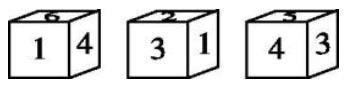
-
16、将正方体切去一块后,得到的如图所示的几何体有个面,有个顶点,有条棱.

-
17、如图所示是某个立体图形的展开图,请你从不同的角度描述这个几何体的特点(写出三点):.

-
18、用小立方块搭成的几何体,从正面和从上面看到的形状图如图所示,则搭成这样的几何体需要小立方块的块数为( )
 A、最多需要8块,最少需要6块 B、最多需要9块,最少需要6块 C、最多需要8块,最少需要7块 D、最多需要9块,最少需要7块
A、最多需要8块,最少需要6块 B、最多需要9块,最少需要6块 C、最多需要8块,最少需要7块 D、最多需要9块,最少需要7块 -
19、用5个大小相同的小正方体搭一个几何体,其从正面和左面看到的图形如图②所示,现将其中4个小正方体按图①所示方式摆放,则最后一个小正方体应放在( )
 A、①号位置 B、②号位置 C、③号位置 D、④号位置
A、①号位置 B、②号位置 C、③号位置 D、④号位置 -
20、用大小相同的小立方体搭成如图所示的几何体,现拿掉其中的一个小立方体后,从左面看这个几何体得到的平面图形与拿掉前相同,则这个被拿掉的小立方体可以是( )
 A、②或④ B、②或③ C、③②或① D、④③或②
A、②或④ B、②或③ C、③②或① D、④③或②