北师大版数学八年级上册单元分层检测卷第二章《实数》B卷

试卷更新日期：2025-09-08 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列运算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{2} \times \sqrt{5} = \sqrt{10}$ C、 $2 \div \sqrt{2} = 1$ D、 $\sqrt{(- 5)^{2}} = - 5$

查看试题解析
2. 已知数轴上点A所表示的数是 $\sqrt{2}$ ，则与点A相距2个单位长度的点表示的数是（）

A、 $\sqrt{2} + 2$ 或 $\sqrt{2} - 2$ B、 $2 + \sqrt{2}$ 或 $2 - \sqrt{2}$ C、 $\sqrt{2} + 2$ D、 $\sqrt{2} - 2$

查看试题解析
3. 公元前5世纪，毕达哥拉斯学派的一个成员发现了一个新数——无理数 $\sqrt{2}$ .他的发现，在当时的数学界掀起了一场巨大风暴，导致西方数学史上的“第一次数学危机”.请估计 $\sqrt{2}$ 的值在（）

A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间

查看试题解析
4. 已知 $1 < x < 2$ ，化简 $\sqrt{{(x - 1)}^{2}} + | x - 2 |$ 的结果为（）

A、 $- 1$ B、1 C、 $2 x - 3$ D、 $3 - 2 x$

查看试题解析
5. 已知 $a = \sqrt{5} ， b = 2 ， c = \sqrt{3}$ ，则a、b、c的大小关系是（）

A、 $b > a > c$ B、 $a > c > b$ C、 $a > b > c$ D、 $b > c > a$

查看试题解析
6. 已知 $2 a$ 的平方根是 $\pm 2$ ， $3$ 是 $3 a + b$ 的立方根，则 $a - 2 b$ 的值是（）

A、 $- 20$ B、 $- 25$ C、 $- 30$ D、 $- 40$

查看试题解析
7. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °, B C = 2, A C = 1, B C$ 在数轴上，以点 $B$ 为圆心， $A B$ 的长为半径画弧，交数轴于点 $D$ ，则点 $D$ 表示的数是（）

A、 $2 - \sqrt{5}$ B、 $\sqrt{5}$ C、 $\sqrt{5} - 2$ D、 $2 - \sqrt{3}$

查看试题解析
8. 规定用符号[m]表示m 的整数部分，如： $[\frac{2}{3}] = 0, [3.14] = 3,$ 若 $[5 + \sqrt{3}] = a, [7 - \sqrt{3}] = b,$ ，则a+b的值为（）

A、9 B、10 C、11 D、12

查看试题解析
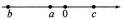9. 如果实数a，b，c在数轴上的位置如图所示：，那么代数式 $\sqrt{a^{2}} - ∣ a + b ∣ +$ $\sqrt{{(c - a)}^{2}} + ∣ b + c ∣$ 可以化简为（）.

A、2c-a B、2a-2b C、-a D、a

查看试题解析
10. 按如图所示的程序计算，若开始输入的值为25，则最后输出的 $y$ 值是（）

A、 $\sqrt{5}$ B、 $\pm \sqrt{5}$ C、 $\pm 5$ D、5

查看试题解析

二、填空题（每题3分，共18分）

11. 已知实数x，y满足 $|x - 4| + \sqrt{y + 11} = 0$ ，则 $x - y + 1$ 的值为．

查看试题解析
12. 我们知道 $\sqrt{3}$ 是无理数，而无理数是无限不循环小数，它的小数部分我们不可能全部地写出来，但是由于 $1 < \sqrt{3} < 2$ ，所以 $\sqrt{3}$ 的整数部分为1，小数部分为 $\sqrt{3} - 1$ 。根据以上的内容，解答下面的问题：若 $\sqrt{7}$ 的小数部分为a， $\sqrt{26}$ 的整数部分为b，则 $a + b - \sqrt{7}$ 的值是。

查看试题解析
13. 当 $a < - 1$ 时， $\sqrt{(a + 1)^{2}} =$ ．

查看试题解析
14. 已知 $y = \sqrt{2 x - 5} + \sqrt{5 - 2 x} - 3$ ，则 $2 x y$ 的值为．

查看试题解析
15. 如图所示，长方形内两个相邻正方形的面积分别为4和2，则阴影部分的面积为.

查看试题解析
16. 如图，正方形ABCD的面积为3，点A在数轴上，且表示的数为－2，以点A为圆心，AB长为半径画弧，与数轴交于点E（点E在点A的右侧），则点E所表示的数为．

查看试题解析

三、解答题（共8题，共72分）

17. 计算：

(1)、 $\sqrt{18} - \sqrt{2} + 6 \sqrt{\frac{1}{2}}$

(2)、 $\sqrt{72} \times \sqrt{3} - \sqrt{\frac{1}{5}} \times \sqrt{30}$

查看试题解析
18. 计算：

(1)、 $\frac{1}{2 + \sqrt{3}} + \sqrt{12} - {(\frac{\sqrt{3}}{3})}^{- 1} .$

(2)、 $2 \sqrt{\frac{1}{3}} \times \sqrt{9} - \sqrt{12} + \sqrt[3]{\frac{7}{8} - 1} .$

查看试题解析
19. 已知 $5 a + 2$ 的立方根是 $3$ ， $3 a + b - 1$ 的算术平方根是 $4$ ， $c$ 是 $\sqrt{13}$ 的整数部分，求 $3 a - b + c$ 的平方根．

查看试题解析
20. 阅读下面的文字，解答问题．
例如：∵ $\sqrt{4} < \sqrt{7} < \sqrt{9}$ ，即 $2 < \sqrt{7} < 3$ ，
∴ $\sqrt{7}$ 的整数部分为2，小数部分为 $\sqrt{7} - 2$ ，
请解答：

(1)、 $\sqrt{15}$ 的整数部分是；

(2)、已知： $8 - \sqrt{15}$ 小数部分是 $m$ ， $8 + \sqrt{15}$ 小数部分是 $n$ ，且 ${(x - 1)}^{2} - m = n$ ，求 $x$ 的值．

查看试题解析
21. 已知5a+2的立方根是3，3a+b-1的算术平方根是4，c是 $\sqrt{13}$ 的整数部分.

(1)、求a，b，c的值；

(2)、求3a-b+c的平方根.

查看试题解析
22. 魔方又叫鲁比克方块，与华容道、独立钻石棋一同被称为智力游戏界的三大不可思议、如图（1）是一个4阶魔方，由四层完全相同的64个小正方体组成，体积为 ${64cm}^{3}$ ．

(1)、求组成这个4阶魔方的小正方体的棱长．

(2)、若图（1）中的四边形 $A B C D$ 是一个正方形，求该正方形的面积及边长．

(3)、若把图（1）中正方形 $A B C D$ 放在数轴上，如图（2），使得点A与表示1的点重合，那么点D在数轴上表示的数为________，这个数的绝对值是．

查看试题解析
23. 我们知道， $（ \sqrt{3} ）^{2} = 3$ ， $(3 + \sqrt{5}) (3 - \sqrt{5}) = 3^{2} - {(\sqrt{5})}^{2} = 4$ ， …如果两个含有二次根式的非零代数式相乘，它们的积不含有二次根式，就说这两个非零代数式互为有理化因式.如 $3 + \sqrt{5}$ 与 $3 - \sqrt{5}$ 互为有理化因式.利用这种方法，可以将分母中含有二次根式的代数式化为分母是有理数的代数式，这个过程称为分母有理化，例如： $\frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{\sqrt{3}}{3}$ ， $\frac{1}{2 - \sqrt{3}} = \frac{2 + \sqrt{3}}{(2 - \sqrt{3}) (2 + \sqrt{3})} = \frac{2 + \sqrt{3}}{1} = 2 + \sqrt{3}$ .

(1)、 $\frac{2}{\sqrt{5}}$ 分母有理化的结果是；

(2)、 $\frac{1}{\sqrt{11} + \sqrt{10}}$ 分母有理化的结果是；

(3)、 $\frac{1}{\sqrt{n + 1} - \sqrt{n}}$ 分母有理化的结果是；

(4)、利用以上知识计算： $\frac{1}{1 + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{5}} + \frac{1}{\sqrt{5} + \sqrt{7}} + ⋯ + \frac{1}{\sqrt{2021} + \sqrt{2023}}$ .

查看试题解析
24. 阅读材料，完成下列任务：
【材料一】 $∵ 4 < 6 < 9$ ， $∴ \sqrt{4} < \sqrt{6} < \sqrt{9}$ ，即 $2 < \sqrt{6} < 3$ ， $∴ \sqrt{6}$ 的整数部分为 2，小数部分为 $\sqrt{6} - 2$ .
【材料二】若正方形面积为 105，则它的边长为 $\sqrt{105}$ . 我们可以按照以下方法求得 $\sqrt{105}$ 近似值：
$∵ 100 < 105 < 121$ ， $∴ \sqrt{100} < \sqrt{105} < \sqrt{121}$ ，即 $10 < \sqrt{105} < 11$ ，
$∴$ 设 $\sqrt{105} = 10 + x$ ，其中 $0 < x < 1$ ，
如图 1，画出边长为 $10 + x$ 的正方形，根据图中面积，得 $1 0^{2} + 2 \times 10 x + x^{2} = 105$ ，
$∵ x^{2}$ 较小，
$∴$ 忽略 $x^{2}$ ，得： $1 0^{2} + 2 \times 10 x \approx 105$ ，解得 $x \approx 0.25$ ， $∴ \sqrt{105} = 10 + x \approx 10.25$ .
【探究问题】

(1)、利用材料一中的方法， $\sqrt{31}$ 的整数部分是，小数部分是；

(2)、利用材料二中的方法，探究 $\sqrt{149}$ 的近似值（要求写出求解过程，结果精确到 0.01）；

(3)、【思维拓展】
a是 $\sqrt{17} - 1$ 的小数部分，b是 $6 - \sqrt{17}$ 的小数部分，则 $(a + b)^{2025}$ 的值是多少？

(4)、探究 $\sqrt{223}$ 的近似值，直接写出结果： $\sqrt{223} \approx$ （结果精确到 0.01）

查看试题解析

北师大版数学八年级上册单元分层检测卷第二章 《实数》B卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共8题，共72分）

北师大版数学八年级上册单元分层检测卷第二章《实数》B卷