浙教版数学八年级上册第3章 一元一次不等式 单元检测基础卷
试卷更新日期:2025-09-08 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 若 , 下列运用不等式基本性质变形正确的是( )A、 B、 C、 D、2. 不等式组的解是( )A、 B、 C、 D、3. 不等式组的解集在数轴上表示正确的是( )A、
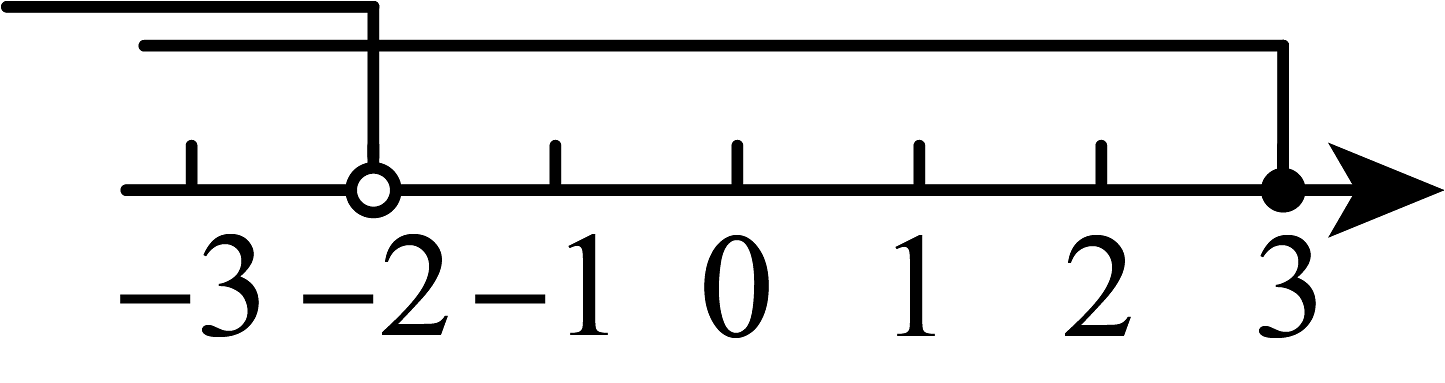 B、
B、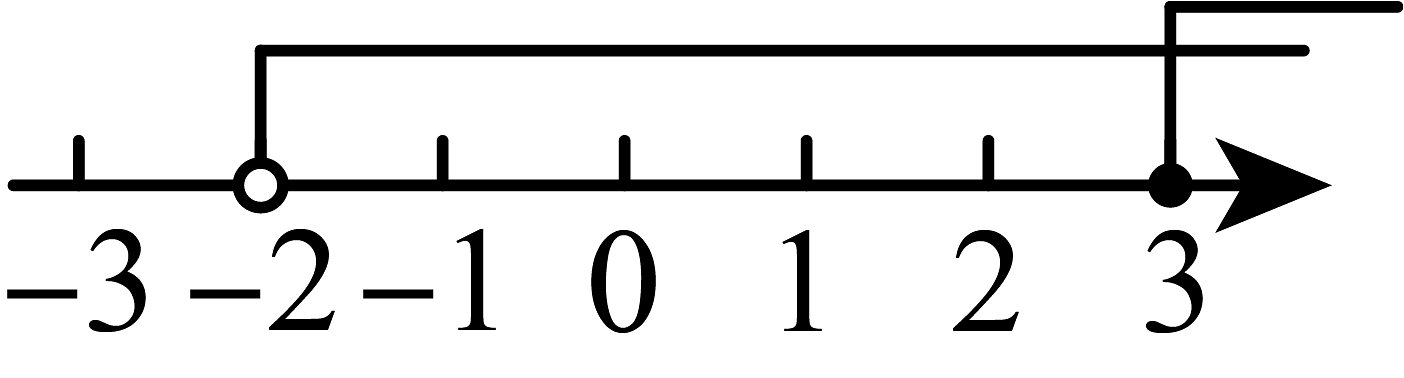 C、
C、 D、
D、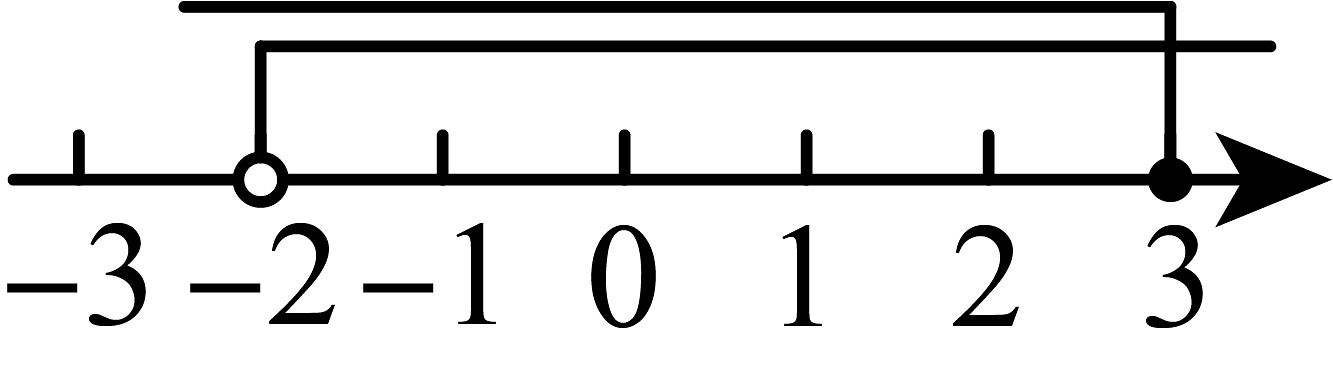 4. 下列选项中,不是不等式x-3<6-2x的一个解的是( ).A、-3 B、 C、 D、35. 一个不等式的解集为x≤1,那么在数轴上表示正确的是( )A、
4. 下列选项中,不是不等式x-3<6-2x的一个解的是( ).A、-3 B、 C、 D、35. 一个不等式的解集为x≤1,那么在数轴上表示正确的是( )A、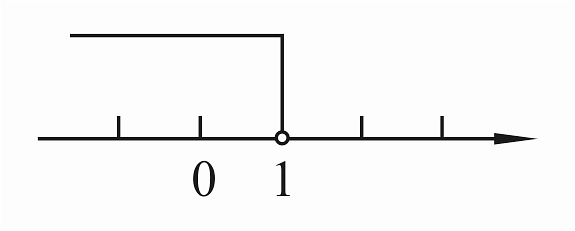 B、
B、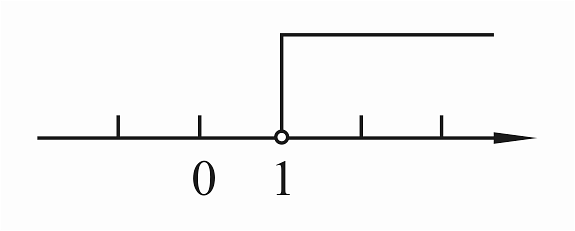 C、
C、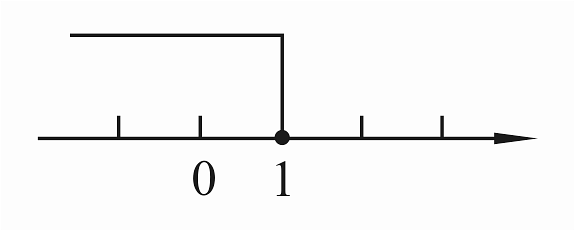 D、
D、 6. 若不等式组的解为 , 则下列各式正确的是( )A、 B、 C、 D、7. 将已知关于x的不等式的解集为 , 则a的取值范围是( )A、 B、 C、 D、8. 某电梯乘载的重量超过1000公斤时会响起警示音,小刚、小明的体重分别为55公斤、70公斤.小刚、小明依序进入电梯,小刚走进后,警示音没响,小明走进后,警示音响起.设两人没进入电梯前已乘载的重量为x公斤,则x满足( )A、 B、 C、 D、9. 已知关于的不等式组的整数解共有4个,则的取值范围是( )A、 B、 C、 D、10. 从3, , , 1,这5个数中,随机抽取一个数记为a , 若数a使关于x的不等式组无解,且使关于x的分式方程有整数解,那么这5个数中所有满足条件的a的值之积是( )A、 B、3 C、 D、
6. 若不等式组的解为 , 则下列各式正确的是( )A、 B、 C、 D、7. 将已知关于x的不等式的解集为 , 则a的取值范围是( )A、 B、 C、 D、8. 某电梯乘载的重量超过1000公斤时会响起警示音,小刚、小明的体重分别为55公斤、70公斤.小刚、小明依序进入电梯,小刚走进后,警示音没响,小明走进后,警示音响起.设两人没进入电梯前已乘载的重量为x公斤,则x满足( )A、 B、 C、 D、9. 已知关于的不等式组的整数解共有4个,则的取值范围是( )A、 B、 C、 D、10. 从3, , , 1,这5个数中,随机抽取一个数记为a , 若数a使关于x的不等式组无解,且使关于x的分式方程有整数解,那么这5个数中所有满足条件的a的值之积是( )A、 B、3 C、 D、二、填空题(每题3分,共18分)
-
11. 若 , 则(填“>”或“<”).12. 根据下列数量关系列不等式: 的 5 倍不大于 4 的不等式是。13. 要说明命题“若 , 则”是假命题,反例的值可以是(写出一个即可).14. 若关于x的不等式只有3个正整数解,则m的取值范围是 .15. 小明准备用零花钱购买一个学生眼镜,他已经存有60元,从现在起计划每月平均存25元.他想购买的这款眼镜至少需要480元,如果存钱个月,不等式可列为 .16. 若关于x的不等式组恰有4个整数解,关于t的分式方程的解也为整数,则所有满足条件的整数a的和为 .
三、解答题(共8题,共72分)
-
17. 在数轴上表示下列不等式:(1)、x<5;(2)、x≥-3;(3)、 - 5<x≤1。18. 解下列不等式(组),并把解在数轴上表示出来.(1)、;(2)、 .19. 已知代数式(1)、当x取何值时,它的值为负数?(2)、当x取何值时,它的值为非负数?20. 某商店为了促销某种商品,将定价为5元的商品按下列方式优惠销售:若购买不超过4件,按原价付款;若一次性购买4件以上,超过部分打八折.现有37元钱,最多可以购买该商品多少件?21. 为全面落实长沙市“三高四新”美好蓝图,市政府计划对城区道路进行改造,现安排甲、乙两个工程队完成.已知甲队的工作效率是乙队工作效率的2倍,甲队改造400米的道路比乙队改造同样长的道路少用5天.(1)、甲、乙两工程队每天能改造道路的长度分别是多少米?(2)、若甲队工作一天需付费用5万元,乙队工作一天需付费用3万元,如需改造的道路全长1000米.改造总费用不超过65万元,至少安排甲队工作多少天?