相关试卷

1、用48米长的木料制作如图所示的矩形窗框(横档 EF，GH 也用木料)，其中AB∥EF∥GH∥CD.若要使窗框ABCD 的面积最大，则AB 的长为( )

A、6米 B、8米 C、12 米 D、4 $\sqrt{3}$

查看解析
2、某班数学兴趣小组对函数 $y = ∣ x^{2} -$ 2x|的图象和性质进行了探究，探究过程如下：

(1)、自变量x 的取值范围是全体实数，x与y的几组对应值列表如下：
x
…
-1
-0.5
0
0.5
1
1.5
2
2.5
3
…
y
…
3
m
0
0.75
1
0.75
0
1.25
3
…
求上表中m 的值.

(2)、根据(1)中的数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请画出该函数图象的另一部分.

(3)、观察函数图象，写出该函数的一条性质.

(4)、通过进一步探究函数图象，解决下列问题：
①方程 $∣ x^{2} - 2 x ∣ = \frac{1}{2}$ 有个实数根.
②在(2)的平面直角坐标系中画出直线y=-x+1，根据图象及(1)中的数据可知，方程 $∣ x^{2} - 2 x ∣ = - x + 1$ 的一个正实数根约为 (结果精确到0.1).

查看解析
3、如图，二次函数 $y = a x^{2} + b x + c$ 的图象过A(2，0)，B(0，-1)和C(4，5)三点.

(1)、求二次函数的表达式.

(2)、设二次函数的图象与x轴的另一个交点为D，求点 D 的坐标.

(3)、在同一平面直角坐标系中画出直线y=x+1，并写出当x在什么范围内时，一次函数的值大于二次函数的值.

查看解析
4、规定：如果两个函数的图象关于y轴对称，那么称这两个函数互为“Y函数”.例如：函数y=x+3与y=-x+3互为“Y 函数”.若函数 $y = \frac{k}{4} x^{2} + (k - 1) x + k - 3$ 的图象与x轴只有一个交点，则它的“Y函数”图象与x 轴的交点坐标为.

查看解析
5、二次函数 $y = x^{2} + b x$ 的图象如图所示，对称轴为直线x=1.若关于x 的一元二次方程 $x^{2} + b x - t = 0$ (b，t为实数)在-1<x<4的范围内有解，则t 的取值范围是.

查看解析
6、已知抛物线y=a(x-1)(x-5)+c(a≠0)与x 轴的一个交点为(2，0)，则方程 $x^{2} + 5 =$ $6 x - \frac{c}{a}$ 的解为 .

查看解析
7、数形结合思想如图，抛物线 $y = a x^{2} +$ bx+c(a≠0)的对称轴为直线x=2.若x₁ ， x₂是一元二次方程 $a x^{2} +$ bx+c=0(a≠0)的两个根，且x₁＜x_2，-1＜x₁<0，则下列说法中，正确的是( )

A、 $x_{1} + x_{2} < 0$ B、 $4 < x_{2} < 5$ C、 $b^{2} - 4 a c < 0$ D、ab>0

查看解析
8、已知二次函数 $y = x^{2} + m x + m^{2} - 3 ($ 1为常数，且m>0)的图象过点 P(2，4).

(1)、求m 的值.

(2)、试判断二次函数 $y = x^{2} + m x + m^{2} - 3$ 的图象与x 轴交点的个数，并说明理由.

查看解析
9、如图，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的对称轴为直线x=1，与x轴分别交于点(m，0)，(n，0)，m $a x^{2} + b x + c - 1 = 0$ 的两个实数根分别为x₁ ， x₂ ，且. $x_{1} < x_{2} ，$ ，则x₁(填“>”或“<”，下同)m，x₂n.

查看解析
10、炮弹从炮口射出后飞行的高度h(m)与飞行的时间t(s)之间的函数表达式为 $h = \frac{1}{2} v_{0} t -$ 5t² ，其中 v₀(m/s)是发射时的初速度.当 $v_{0} = 300$ 时，炮弹飞行的最大高度为m，该炮弹在空中飞行了s后落到地面上.

查看解析
11、一元二次方程 $2 x^{2} - x - 2 = 0$ 的近似根可以看做是两个函数图象交点的横坐标，则两个函数的表达式可以为( )

A、 $y = 2 x^{2}$ 和y=x+2 B、 $y = 2 x^{2}$ 和y=-x-2 C、 $y = - 2 x^{2}$ 和y=x+2 D、 $y = - 2 x^{2}$ 和y=-x+2

查看解析
12、如图，点A(2.18，-0.51)，B(2.68，0.54)在二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象上，则关于x 的方程 $a x^{2} + b x + c = 0$ 的一个近似值可能是( )

A、1.5 B、2.18 C、2.45 D、2.6

查看解析
13、已知A(1，0)，B(0，-1)，C(-1，2)，D(2，—1)，E(4，2)五个点，抛物线 $y = a {(x - 1)}^{2} + k (a⟩ 0)$ 经过其中三个点.

(1)、求证：C，E两点不可能同时在抛物线 $y = a {(x - 1)}^{2} + k (a⟩ 0)$ 上.

(2)、点A 是否在抛物线 $y = a {(x - 1)}^{2} + k$ (a>0)上? 请说明理由.

(3)、求a 和k 的值.

查看解析
14、如图，直线 y=-3x+3与x 轴、y 轴分别交于点A，B，抛物线 $y = a {(x - 2)}^{2} + k$ 经过点A，B，并与x 轴交于另一点C，其顶点为 P.

(1)、求a，k 的值及点C 的坐标.

(2)、若抛物线的对称轴上有一点 Q，且使得△ABQ 是以AB 为底边的等腰三角形，求点 Q 的坐标.

查看解析
15、如图，点 P(a，3)在抛物线y=4-(6-x)²上，且在抛物线的对称轴右侧.

(1)、写出抛物线的对称轴，并求a 的值.

(2)、平移此抛物线，使平移后的抛物线对应的函数表达式为 $y = - {(x - 3)}^{2} .$ 求顶点移动的最短路程.

查看解析
16、如图，抛物线 $y_{1} = - \frac{1}{2} x^{2} + 1$ 与 $y_{2} = - \frac{1}{2} x^{2} -$ 1分别经过点(-2，-1)，(2，-3)，则它们与平行于 y 轴的两条平行线围成的涂色部分的面积为.

查看解析
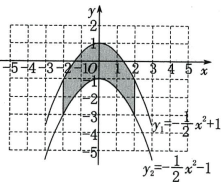
17、在平面直角坐标系中，抛物线 y= $- {(x + 6)}^{2} + 5$ 与 x 轴相交于(a，0)，(b，0)两点，其中a<b.现在将此抛物线向上平移，平移后的抛物线与x 轴相交于(c，0)，(d，0)两点，其中c<d，则下列叙述正确的是( )

A、a+b=c+d，b-a<d-c B、a+b=c+d，b-a>d-c C、a+b<c+d，b-a<d-c D、a+b<c+d，b-a>d-c

查看解析
18、将抛物线 $y = a x^{2} - 1$ 平移后与抛物线 y= $a {(x - 1)}^{2}$ 重合，抛物线 $y = a x^{2} - 1$ 上的点A(2，3)同时平移到点 A^' ，则点 A^'的坐标为( )

A、(3，4) B、(1，2) C、(3，2) D、(1，4)

查看解析
19、二次函数 $y = {(x + m)}^{2} + n$ 的图象如图所示，则一次函数y=mx+n的图象不经过( )

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看解析
20、把抛物线 $y = a {(x - h)}^{2} + k$ 先向左平移2个单位，再向上平移4个单位，得到抛物线y= $\frac{1}{2} {(x + 1)}^{2} - 1 .$

(1)、试确定a，h，k的值.

(2)、指出抛物线 $y = a {(x - h)}^{2} + k$ 的开口方向、对称轴和顶点坐标.

查看解析

上一页 436 437 438 439 440 下一页跳转

x	…	-1	-0.5	0	0.5	1	1.5	2	2.5	3	…
y	…	3	m	0	0.75	1	0.75	0	1.25	3	…