-
1、 如图,AB 是⊙O的直径,C,D 是⊙O上的点,∠CDB=15°,过点C作⊙O 的切线交AB 的延长线于点E,则 sin E 的值为( )
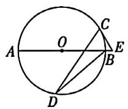 A、12 B、 C、 D、
A、12 B、 C、 D、 -
2、 如图, M是边OA 上一点,以点M 为圆心,3cm为半径作⊙M.当OM=5cm时,⊙M 与直线OB 的位置关系是( )
 A、相离 B、相交 C、相切 D、无法确定
A、相离 B、相交 C、相切 D、无法确定 -
3、 在△ABC 中,若 则△ABC为( )A、直角三角形 B、等边三角形 C、含 60°角的任意三角形 D、顶角是钝角的等腰三角形
-
4、下列物体的影子中,不正确的是( )A、
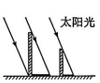 B、
B、 C、
C、 D、
D、
-
5、篆刻是中华传统艺术之一,雕刻印章是篆刻基本功.如图所示为一块雕刻印章的材料,其俯视图为( )
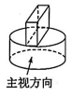 A、
A、 B、
B、 C、
C、 D、
D、
-
6、综合与实践课上,老师让同学们以“三角形的角与三角形的特殊线段”为主题开展数学活动.

 (1)、【操作判断】在△ABC中,∠B=40°,∠C=70°,作∠BAC 的平分线AD交BC于点 D.
(1)、【操作判断】在△ABC中,∠B=40°,∠C=70°,作∠BAC 的平分线AD交BC于点 D.①操作一:在图(1)中,用三角尺作 BC 边上的高AE,垂足为点 E,求∠DAE的度数;
②操作二:如图(2),在 AD 上任取点 F,作FE⊥BC,垂足为点 E,直接写出∠DFE 的度数.
(2)、【迁移探究】如图(3),将操作二中“在AD上任取点 F”改为“在DA 的延长线上任取点F”,其他条件不变,判断∠DFE 的度数是否会发生变化,并说明理由.(3)、【拓展应用】如图(4)、图(5),在△ABC中,∠ABC=α,∠ACB=β,AD 是∠BAC 的平分线,在直线AD 上任取点 F,过点 F 作EF⊥AD与直线 BC 交于点 E,请求出∠DEF 与α,β之间的数量关系. -
7、如图,△ABC中,AD是 BC 边上的高,AE 是∠BAC 的平分线,∠EAD=15°,∠B=50°,求∠C的度数.

-
8、
 (1)、探究:如图(1),在△ABC 中,∠ACB=90°,CD⊥AB 于点 D,若∠B=30°,则∠ACD 的度数是°;(2)、拓展:如图(2),∠MCN=90°,射线 CP 在∠MCN 的内部,点A,B分别在 CM,CN上,分别过点A,B 作AD⊥CP,BE⊥CP,垂足分别为D,E,若∠CBE=70°,求∠CAD 的度数;(3)、应用:如图(3),点A,B 分别在∠MCN 的边CM,CN上,射线CP 在∠MCN 的内部,点D,E在射线 CP 上,连结AD,BE,若∠ADP=∠BEP = 60°, 则 ∠CAD+∠CBE +∠ACB =°.
(1)、探究:如图(1),在△ABC 中,∠ACB=90°,CD⊥AB 于点 D,若∠B=30°,则∠ACD 的度数是°;(2)、拓展:如图(2),∠MCN=90°,射线 CP 在∠MCN 的内部,点A,B分别在 CM,CN上,分别过点A,B 作AD⊥CP,BE⊥CP,垂足分别为D,E,若∠CBE=70°,求∠CAD 的度数;(3)、应用:如图(3),点A,B 分别在∠MCN 的边CM,CN上,射线CP 在∠MCN 的内部,点D,E在射线 CP 上,连结AD,BE,若∠ADP=∠BEP = 60°, 则 ∠CAD+∠CBE +∠ACB =°. -
9、如图,在△ABC 中,AB=8,BC=10,CF⊥AB 于点 F,AD⊥BC 于点D,AD与CF交于点E,∠B=46°.
 (1)、求∠AEC 的度数.(2)、若AD=6,求CF 的长.
(1)、求∠AEC 的度数.(2)、若AD=6,求CF 的长. -
10、在△ABC 中,∠ABC 与∠ACB 的平分线相交于点 P.
 (1)、如图 (1), 若 ∠BPC = α, 则 ∠A =;(用含α的代数式表示)(2)、如图(2),作△ABC 外角∠MBC,∠NCB的平分线交于点 Q,试探究∠Q 与∠BPC 之间的数量关系,并说明理由.
(1)、如图 (1), 若 ∠BPC = α, 则 ∠A =;(用含α的代数式表示)(2)、如图(2),作△ABC 外角∠MBC,∠NCB的平分线交于点 Q,试探究∠Q 与∠BPC 之间的数量关系,并说明理由. -
11、如图,在△ABC 中,∠A=α,∠ABC 的平分线与△ACB 的外角(∠ACD)的平分线交于点A1; ∠A1BC 的 平 分 线 与 △A1CB 的 外 角(∠A1CD)的平分线交于点A2 , …,以此类推,则 .(用含α的式子表示)

-
12、如图,△ABC 的角平分线 BD,CE 相交于点F.
 (1)、若∠A = 54°,∠ABC = 50°,求∠CFD 的度数;(2)、证明:2∠BFC=∠A+180°.
(1)、若∠A = 54°,∠ABC = 50°,求∠CFD 的度数;(2)、证明:2∠BFC=∠A+180°. -
13、如图,在△ABC 中,∠A=52°,∠ABC 与∠ACB 的平分线交于点 D1 , ∠ABD1与∠ACD1的平分线交于点 D2 , …,依次类推,∠ABD3与∠ACD3的平分线交于点D4 , 则∠BD4C 的度数是.

-
14、如图,∠BAD 与)∠BCE的平分线交于点 P,BC 交AD 于 O,CE的反向延长线交AD于D,则∠P 与∠B,∠D 的数量关系是( )
 A、2∠P-∠B+∠D=180° B、2∠P-∠B-∠D=180° C、2∠P+∠B-∠D=180° D、2∠P+∠B+∠D=360°
A、2∠P-∠B+∠D=180° B、2∠P-∠B-∠D=180° C、2∠P+∠B-∠D=180° D、2∠P+∠B+∠D=360° -
15、问题情境:

如图(1)所示的图形像我们常见的学习用品——圆规.我们不妨把这样的图形叫作“规形图”.
(1)、探究发现:观察“规形图”,试探究∠D 与∠BAC,∠B,∠C 之间的数量关系,并说明理由;
(2)、解决问题:请你利用以上结论,解决下列问题:
①如图(2),把一块含45°角的三角尺DEF 放置在△ABC上,使三角尺的两条直角边DE,DF恰好经过点 B,C, 若 ∠A = 40°, 则 ∠ABD +∠ACD=°;
②如图(3),BD平分∠ABP,CD平分∠ACP,若∠A=40°,∠P=130°,则∠D 的度数为.
-
16、如图,∠ABD,∠ACD的平分线交于点 P,若∠A=55°,∠D=15°,则∠P 的度数为( )
 A、15° B、20° C、25° D、30°
A、15° B、20° C、25° D、30° -
17、如图,将三角形纸片ABC 沿 DE 折叠,当点 A 落在四边形 BCED的外部点A'处时,测得∠1=70°,∠2=140°,则∠A 的度数为( )
 A、25° B、30° C、35° D、40°
A、25° B、30° C、35° D、40° -
18、如图,△ABC 中,∠A=65°,直线DE 交AB 于点 D,交AC 于点 E,则∠BDE+∠CED=( )
 A、180° B、215° C、235° D、245°
A、180° B、215° C、235° D、245° -
19、如图(1),AB=4 cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P 在线段AB 上以1 cm/s 的速度由A 向B运动,同时点Q 在线段 BD 上由点 B 向点 D 运动.它们运动的时间为ts.
 (1)、若点 Q 的运动速度与点 P 的运动速度相同,当t=1时,△ACP 与△BPQ 是否全等? 请说明理由,并判断此时线段 PC 和线段PQ 的位置关系.(2)、如图(2),将“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA”,其他条件不变,设点 Q 运动速度为x cm/s,是否存在实数x,使得△ACP 与△BPQ 全等?若存在,求出相应的x,t的值;若不存在,请说明理由.
(1)、若点 Q 的运动速度与点 P 的运动速度相同,当t=1时,△ACP 与△BPQ 是否全等? 请说明理由,并判断此时线段 PC 和线段PQ 的位置关系.(2)、如图(2),将“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA”,其他条件不变,设点 Q 运动速度为x cm/s,是否存在实数x,使得△ACP 与△BPQ 全等?若存在,求出相应的x,t的值;若不存在,请说明理由. -
20、如图,某村庄有一块五边形的田地,即五边形ABCDE,其中AB=AE=60 m,CD=70 m,∠ABC=∠AED=90°,连结AC,AD,∠BAE=2∠CAD.
 (1)、∠BAC, ∠DAE与∠CAD之间的数量关系为;(2)、为保护田内农作物不被牲畜踩踏,村里决定给这块田地的五边上围一圈栅栏,已知每米栅栏的建造成本是50元,则建造栅栏共需花费多少元?(3)、在△ADE和△ABC区域种上小麦,已知每平方米田地的小麦播种量为21克,则需要提前准备小麦种子千克.
(1)、∠BAC, ∠DAE与∠CAD之间的数量关系为;(2)、为保护田内农作物不被牲畜踩踏,村里决定给这块田地的五边上围一圈栅栏,已知每米栅栏的建造成本是50元,则建造栅栏共需花费多少元?(3)、在△ADE和△ABC区域种上小麦,已知每平方米田地的小麦播种量为21克,则需要提前准备小麦种子千克.