4.6 利用相似三角形测高-北师大版数学九年级上册

试卷更新日期：2025-11-09 类型：同步测试

进入出卷网下载

一、选择题

1. 在相同的时刻，太阳光下物高与影长成正比．如果高为1.5米的人的影长为2.5米，那么影长为30米的旗杆的高是（　　）.

A、18米 B、16米 C、20米 D、15米

查看试题解析
2. 如图，在同一时刻，身高1.6米的小丽在阳光下的影长为2.5米，一棵大树的影长为5米，则这棵树的高度为（）

A、7.8米 B、3.2米 C、2.30米 D、1.5米

查看试题解析
3. 图1是装了液体的高脚杯示意图（数据如图），用去一部分液体后如图2所示，此时液面 $A B =$ （）

A、 $1 cm$ B、 $2 cm$ C、 $3 cm$ D、 $4 cm$

查看试题解析
4. 大约在两千四五百年前，墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录：“景到，在午有端，与景长，说在端”.如图所示的小孔成像实验中，若物距为10cm，像距为15cm，蜡烛火焰倒立的像的高度是8cm，则蜡烛火焰的高度是（）cm

A、 $\frac{9}{2}$ B、 $\frac{16}{3}$ C、6 D、8

查看试题解析
5. 图 1 是捣谷物的＂碓＂，图 2 是其示意图， $O$ 为转动支点， $C D ⊥ A B$ 于点 $B, A B$ 与水平线 $M N$ 夹角 $∠ B O M = 30^{\circ}, B C = 40 c m, O B = 120 c m$ ， $O A = 40 c m$ ．当点 $C$ 绕点 $O$ 旋转下落到 $M N$ 上时，点 $A$ 上升（）

A、 $2 \sqrt{10} cm$
B、 $(20 - 2 \sqrt{10}) c m$ C、 $4 \sqrt{10} cm$
D、 $(20 - 4 \sqrt{10}) c m$

查看试题解析
6. 天坛是古代帝王祭天的地方，其中最主要的建筑就是祈年殿．老师希望同学们利用所学过的知识测量祈年殿的高度，数学兴趣小组的同学们设计了如图所示的测量图形，并测出竹竿 $A B$ 长2米，在太阳光下，它的影长 $B C$ 为 $1.5$ 米，同一时刻，祈年殿的影长 $E F$ 约为 $28.5$ 米．请你根据这些数据计算出祈年殿 $D E$ 的高度约（）米．

A、20 B、15 C、28 D、38

查看试题解析
7. 如图1是《九章算术》中记载的“测井深”示意图，译文指出：“如图2，今有井直径 $C D$ 为5尺，不知其深 $A D$ ，立5尺长的木 $C E$ 于井上，从木的末端E点观察井水水岸A处，测得“入径 $C F$ ”为4寸，问井深 $A D$ 是多少？（其中1尺 $= 10$ 寸）”根据译文信息，则井深 $A D$ 为（　　）

A、500寸 B、525寸 C、50寸 D、575寸

查看试题解析
8. 如图，一块材料的形状是锐角三角形 $A B C$ ，边 $B C$ 长 $12 cm, B C$ 边上的高 $A D$ 为 $10cm$ ，把它加工成正方形零件，使正方形的一边 $G H$ 在 $B C$ 上，其余两个顶点E、F分别在 $A B 、 A C$ 上，则这个正方形零件的边长是（）

A、 $5 cm$ B、 $\frac{60}{11} cm$ C、 $6 cm$ D、 $\frac{72}{11} cm$

查看试题解析

二、填空题

9. 如图，某小区地下车库入口栏杆短臂 $A O = 1.2 m$ ，长臂 $O B = 3.6 m$ ，当短臂端点A下降 $0.6 m$ 时，长臂端点B升高 m．

查看试题解析
10. 四分仪是一种十分古老的测量仪器．其出现可追溯到数学家托勒密的《天文学大成》图1是描述古代测量员用四分仪测量一方井的深度，将四分仪置于方井上的边沿，通过观衡杆测望井底点 $F$ 、窥衡杆与四分仪的一边 $B C$ 交于点 $H$ ．如图2，四分仪为正方形 $A B C D$ ．方井为矩形 $B E F G$ ．若测量员从四分仪中读得 $A B$ 为 $0.8. B H$ 为0.4实地测得 $B E$ 为2，则井深 $B G$ 为．

查看试题解析
11. 如图，小明同学用木棍制成的 $Rt △ D E F$ 测量旗杆的高度 $A B$ ．他调整自己的位置，使斜边 $D E$ 保持与地面 $A C$ 平行，直角边 $D F$ 与点 $B$ 在同一直线上．已知 $D F = 2$ 米， $E F = 1.5$ 米，斜边 $D E$ 离地面的高度 $D C = 1.5$ 米， $A C = 14$ 米，则旗杆的高度 $A B =$ 米．

查看试题解析
12. 《九章算术》是我国古代数学名著，书中有如下问题： “今有井径 $5$ 尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸．问井深几何？”意思是：如图，井径 $B E = 5$ 尺，立木高 $A B = 5$ 尺， $B D = 4$ 寸 $= 0.4$ 尺，则井深 $x$ 为尺．

查看试题解析
13. 如图，在某小区内拐角处的一段道路上，有一儿童在C处玩耍，一辆汽车从被楼房遮挡的拐角另一侧的A处驶来（ $C M ⊥ D M$ ， $B D ⊥ D M$ ， $B C$ 与 $D M$ 相交于点O），已知 $O M = 4$ 米， $C O = 5$ 米， $D O = 3$ 米， $A O = \sqrt{73}$ 米，则汽车从A处前行的距离 $A B =$ 米时，才能发现C处的儿童．

查看试题解析

三、解答题

14. 如图，在 $△ A B C$ 中，点 $D$ 在 $A B$ 边上，点 $E$ 在 $A C$ 边上，且 $∠ A E D = ∠ B$ ，若 $A E = 3$ ， $E C = 1$ ， $A D = 2$ ，求 $A B$ 的长．

查看试题解析
15. 如图，路灯（P点）距地面8米，小明在距路灯的底部（O点）20米的A点时，测得此时他的影长 $A M$ 为5米．

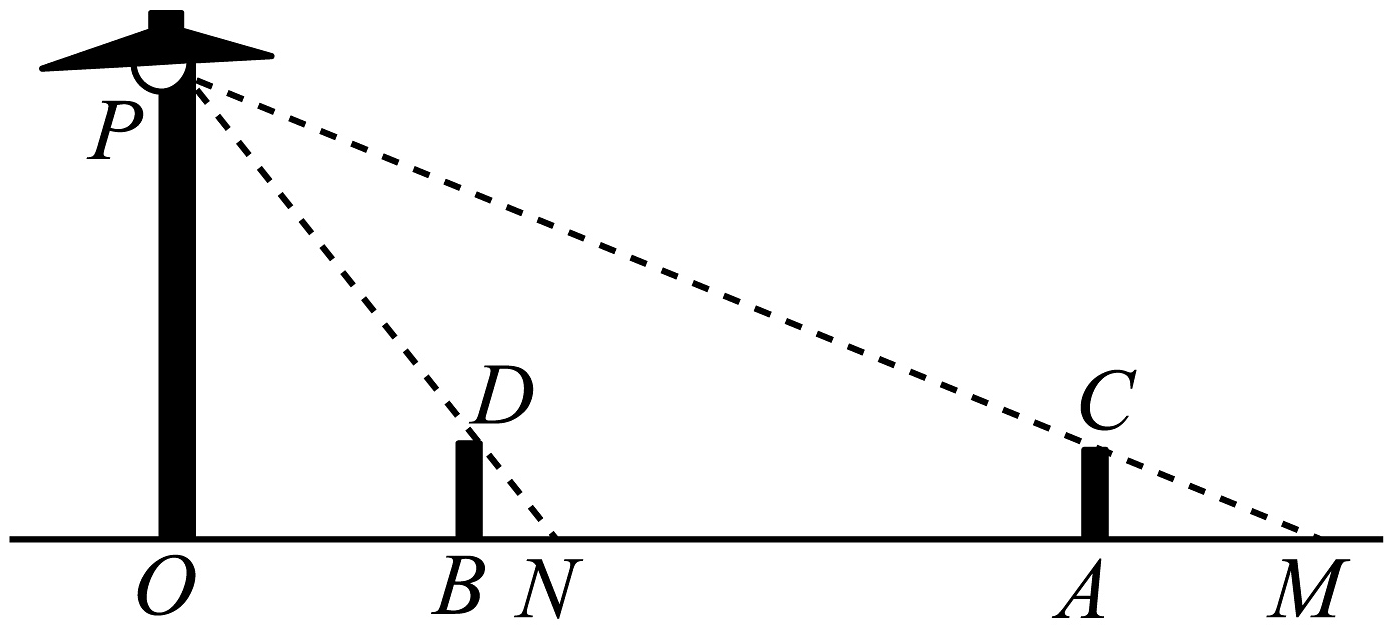(1)、求小明的身高；

(2)、小明沿 $O A$ 所在的直线行走14米到B点时，身影的长度是变长了还是变短了？变长或变短了多少米？

查看试题解析
16. 如图，河的两岸是平行的，两岸边各有一排树，每排树相邻两棵的间距是10m，在距离岸边16m的A处看对岸，可以看到对岸的两棵树 $B 、 C$ 的树干恰好被这岸的两棵树 $E 、 D$ 的树干遮住，又知这岸的两棵树 $D 、 E$ 之间有一棵树，对岸的两棵树 $B 、 C$ 之间有四棵树，请你根据这些条件求出河宽．

查看试题解析
17. 如图所示，某测量工作人员头顶A与标杆顶点F、电视塔顶端E在同一直线上，已知此测量人员的头顶距地面的高 $A B$ 为1.4m，标杆 $F C$ 的长为2.8m，且测量人员与标杆的距离 $B C$ 为3.5m，标杆与电视塔的距离 $C D$ 为6.5m， $A B ⊥ B C$ ， $F C ⊥ B D$ ， $E D ⊥ B D$ ，求电视塔的高 $D E$ ．

查看试题解析
18. 为了加快城市发展，保障市民出行方便，在流经该市的河流上架起一座桥，连通南北，铺就城市繁荣之路.小明和小颖想通过自己所学的数学知识计算该桥AF的长.如图，该桥两侧河岸平行他们在河的对岸选定一个目标作为点A，再在河岸的这一边选出点B和点C，分别在AB，AC的延长线上取点D，E，使得 DE∥BC .经测量BC=80米，DE=140米，且点E到河岸BC的距离为90米，已知AF⊥BC于点F，请你根据提供的数据，帮助他们计算桥AF的长度

查看试题解析
19. 一块直角三角形木板的一条直角边 $A B$ 为1.5米，面积为1.5平方米，要把它加工成一个面积最大的正方形桌面，小明打算按图1的方式进行加工，小华准备按图2的方式进行加工，加工损耗忽略不计，请用学过的知识说明谁的加工方案符合要求？

查看试题解析
20. 小玲和晓静很想知道某塔的高度PQ，于是，他们带着标杆和皮尺进行测量，测量方案如下：如图所示，首先，小玲在 $C$ 处放置一平面镜，她从点 $C$ 沿QC后退，当退行 $1.8 m$ 到 $B$ 处时，恰好在镜子中看到塔顶 $P$ 的像，此时测得小玲眼睛到地面的距离AB为 $1.5 m$ ；然后，晓静在 $F$ 处竖立了一根高 $1.6 m$ 的标杆EF，发现地面上的点 $M$ 、标杆顶点 $E$ 和塔顶 $P$ 在一条直线上，此时测得FM为 $2.4 m ， C F$ 为 $11.7 m$ ，已知 $P Q ⊥ Q M ， A B ⊥ Q M ， E F ⊥ Q M$ ，点Q，C，B，F，M在一条直线上，请根据以上所测数据，计算该塔的高度PQ.

查看试题解析

21. 为了测量一条两岸平行的河流的宽度，三个数学活动小组设计了不同的方案，他们在河南岸的点

B

处测得河北岸的树

A B

恰好在

B

的正北方向，测量方案如下表：

课题	测量河流宽度
工具	测量角度的仪器，标杆，皮尺等
小组	第一小组	第二小组	第三小组
测量方案	观测者从 $B$ 点向东走到 $C$ 点，此时测得点 $C$ 恰好在东南方向上．	观测者从 $B$ 点出发，沿着南偏西 $70 °$ 的方向走到点 $C$ ，此时恰好测得 $∠ A C B = 35 °$ ．	观测者从 $B$ 点向东走到 $O$ 点，在 $O$ 点插上一面标杆，继续向东走一定的路程到达 $C$ 点后，一直向南走到点 $D$ ，使得树、标杆、人在同一直线上．
测量示意图

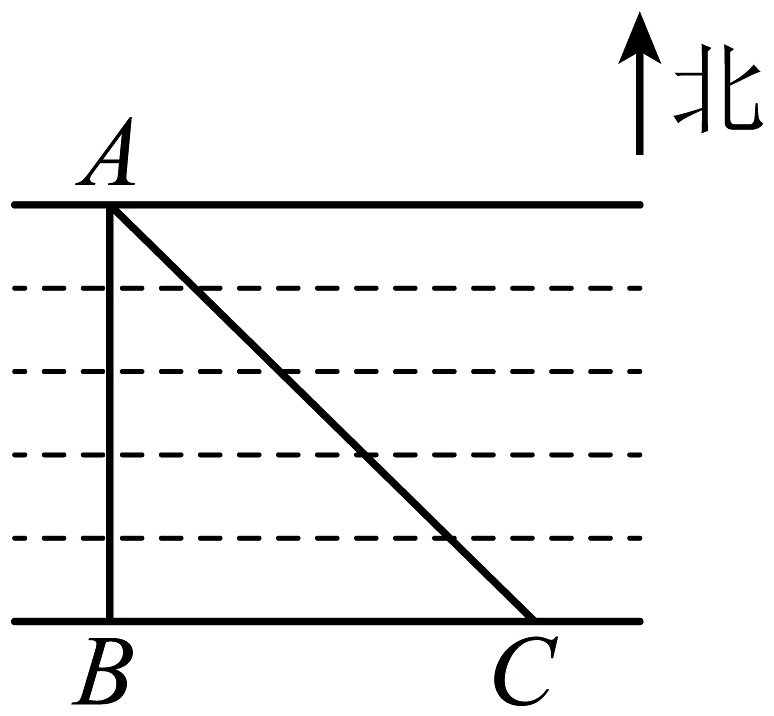
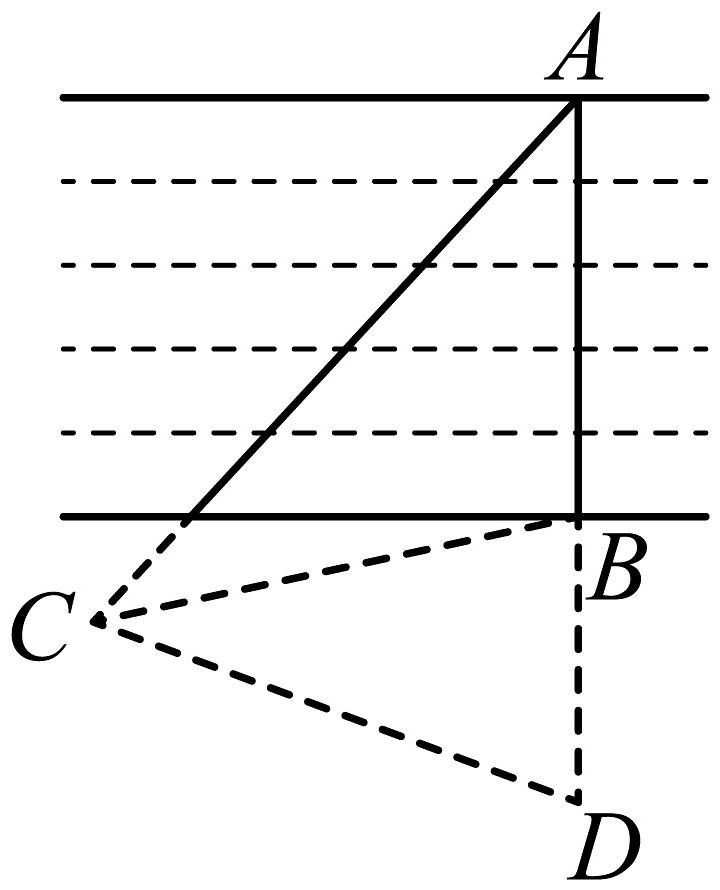
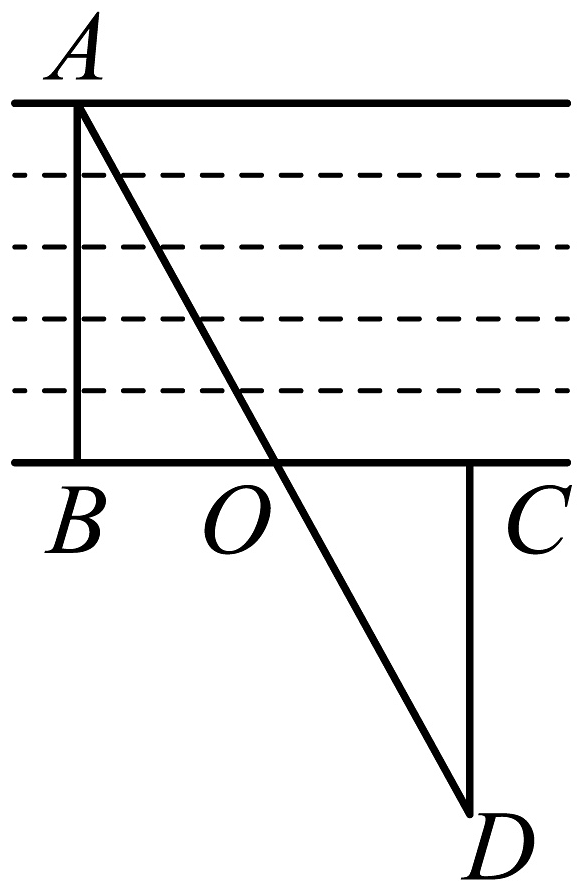(1)、第一小组认为要知道河宽

A B

，只需要知道线段______的长度．

(2)、第二小组测得

B C = 30

米，则

A B =

______米．

(3)、第三小组认为只要测得

B O, O C, C D

就能得到河宽

A B

，你认为第三小组的方案可行吗？如果可行，请给出证明；如果不可行，请说明理由．

查看试题解析

22. 综合与实践：某数学兴趣小组测量一座塔的高度 $A B$ ，有以下两种方案：
方案一：如图1，在距离塔底B点 $45 m$ 远的D处竖立一根高 $1.5 m$ 的标杆 $C D$ ，小明在F处蹲下，他的眼睛所在位置E、标杆的顶端C和塔顶点A三点在一条直线上．已知小明的眼睛到地面的距离 $E F = 0.8 m$ ， $D F = 1 m$ ， $A B ⊥ B M$ ， $C D ⊥ B M$ ， $E F ⊥ B M$ ，点B，D，F，M在同一直线上．
方案二：如图2，小华拿着一把长为 $22 cm$ 的直尺 $C D$ 站在离塔 $A B$ 距离 $45 m$ 的地方（即点E到 $A B$ 的距离为 $45 m$ ）．他把手臂向前伸，尺子竖直， $C D ∥ A B$ ，尺子两端恰好遮住塔 $A B$ （即A，C，E在一条直线上，B，D，E在一条直线上），已知点E到直尺 $C D$ 的距离为 $30 cm$ ．
请你结合上述两个方案，选择其中的一个方案求塔的高度 $A B$ ．

查看试题解析