5.1 投影-北师大版数学九年级上册
试卷更新日期:2025-11-09 类型:同步测试
一、选择题
-
1. 下列哪种影子不是中心投影( )A、月光下房屋的影子 B、晚上在房间内墙上的手影 C、都市霓虹灯形成的影子 D、皮影戏中的影子2. 日晷是我国古代利用日影测定时刻的一种计时仪器, 它由"晷面"和"晷针"组成. 当太阳光 照在日晷上时, 晷针的影子就会投向晷面. 随着时间的推移, 晷针的影子在原面上慢慢地移动,以此来显示时刻。则晷针在晷面上形成的投影是( )
 A、中心投影 B、平行投影 C、既是平行投影又是中心投影 D、不能确定3. 如图是嘉淇在室外用手机拍下大树的影子随太阳转动情况的照片(上午8时至下午5时之间),这五张照片拍摄的时间先后顺序是( )
A、中心投影 B、平行投影 C、既是平行投影又是中心投影 D、不能确定3. 如图是嘉淇在室外用手机拍下大树的影子随太阳转动情况的照片(上午8时至下午5时之间),这五张照片拍摄的时间先后顺序是( ) A、 B、 C、 D、4. 如图,三角板在手电筒光源的照射下形成了投影,三角板与其投影是位似图形,其相似比是 , 若三角板的面积是 , 则其投影的面积是( )
A、 B、 C、 D、4. 如图,三角板在手电筒光源的照射下形成了投影,三角板与其投影是位似图形,其相似比是 , 若三角板的面积是 , 则其投影的面积是( ) A、 B、 C、 D、5. 如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20 m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5 m,两个路灯的高度都是9 m,则两路灯之间的距离是( )
A、 B、 C、 D、5. 如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20 m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5 m,两个路灯的高度都是9 m,则两路灯之间的距离是( ) A、24 m B、25 m C、28 m D、30 m6. 如图,小明居住的小区内有一条笔直的小路,有一盏路灯位于小路上 两点的正中间,晚上,小明由点 处径直走到点 处,他在灯光照射下的影长 与行走路程 之间的变化关系用图象表示大致是( )
A、24 m B、25 m C、28 m D、30 m6. 如图,小明居住的小区内有一条笔直的小路,有一盏路灯位于小路上 两点的正中间,晚上,小明由点 处径直走到点 处,他在灯光照射下的影长 与行走路程 之间的变化关系用图象表示大致是( )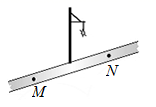 A、
A、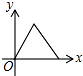 B、
B、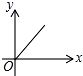 C、
C、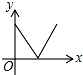 D、
D、 7. 一块三角形纸板如图所示, , , 测得边的中心投影的长为 , 则边的中心投影的长为( )
7. 一块三角形纸板如图所示, , , 测得边的中心投影的长为 , 则边的中心投影的长为( ) A、 B、 C、 D、8. 下列说法正确的是( )A、任意两个位似三角形一定相似 B、物体在任何光线照射下影子的方向都是相同的 C、如果2a=3b , 则 D、点P是长为2的线段AB的黄金分割点,则AP=-1
A、 B、 C、 D、8. 下列说法正确的是( )A、任意两个位似三角形一定相似 B、物体在任何光线照射下影子的方向都是相同的 C、如果2a=3b , 则 D、点P是长为2的线段AB的黄金分割点,则AP=-1二、填空题
-
9. 如图,当太阳光与地面上的树影成45°角时,树影投射在墙上的影高CD等于2米,若树根到墙的距离BC等于8米,则树高AB等于米.
 10. 早在多年前的宋朝,手影就已经作为民间一种有趣的游戏而存在.诗人释惠明在《手影戏》中写到:“三尺生绡作戏台,全凭十指送诙谐.有时明月灯窗下,一笑还从掌握来”.手影戏全凭手影艺人的十指借光弄影,表演各色人物、花草虫鱼、飞禽走兽甚至是寓言故事.如图,手影戏中的手影属于(填“平行投影”或“中心投影”).
10. 早在多年前的宋朝,手影就已经作为民间一种有趣的游戏而存在.诗人释惠明在《手影戏》中写到:“三尺生绡作戏台,全凭十指送诙谐.有时明月灯窗下,一笑还从掌握来”.手影戏全凭手影艺人的十指借光弄影,表演各色人物、花草虫鱼、飞禽走兽甚至是寓言故事.如图,手影戏中的手影属于(填“平行投影”或“中心投影”). 11. 如图,在斜坡的顶部有一铁塔AB,B是CD 的中点,CD 是水平的,在阳光的照射下,塔影DE 留在坡面上.已知铁塔底宽CD=12m,塔影长DE=18m,小明和小华的身高都是1.6m,同一时刻,小明站在点E 处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m 和1m,那么塔高 AB 为m.
11. 如图,在斜坡的顶部有一铁塔AB,B是CD 的中点,CD 是水平的,在阳光的照射下,塔影DE 留在坡面上.已知铁塔底宽CD=12m,塔影长DE=18m,小明和小华的身高都是1.6m,同一时刻,小明站在点E 处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m 和1m,那么塔高 AB 为m. 12. 《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的ABC).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度。如图,是用“矩”测量一个5G信号塔高度的示意图,点A,B,N在同一水平线上,∠ABC和∠ANM均为直角,AM与BC交于点D,测得AB=40cm,BD=30cm,BN=22m,则信号塔MN的高度为m.
12. 《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的ABC).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度。如图,是用“矩”测量一个5G信号塔高度的示意图,点A,B,N在同一水平线上,∠ABC和∠ANM均为直角,AM与BC交于点D,测得AB=40cm,BD=30cm,BN=22m,则信号塔MN的高度为m. 13. 古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔塔顶A的影子处直立一根木杆 , 借助太阳光测金字塔的高度.如图所示,木杆长2米.它的影长是3米,同一时刻测得是201米,则金字塔的高度是米.
13. 古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔塔顶A的影子处直立一根木杆 , 借助太阳光测金字塔的高度.如图所示,木杆长2米.它的影长是3米,同一时刻测得是201米,则金字塔的高度是米.
三、解答题
-
14. 在公园有两座垂直于水平地面且高度不一的圆柱,两座圆柱后面有一堵与地面互相垂直的墙,且圆柱与墙的距离皆为公分.敏敏观察到高度公分矮圆柱的影子落在地面上,其影长为公分;而高圆柱的部分影子落在墙上,如图所示.

已知落在地面上的影子皆与墙面互相重直,并视太阳光为平行光,在不计圆柱厚度与影子宽度的情况下,请回答下列问题:
(1)若敏敏的身高为公分,且此刻她的影子完全落在地面上,则影长为多少公分?
(2)若同一时间量得高圆柱落在墙上的影长为公分,则高圆柱的高度为多少公分?请详细解释或完整写出你的解题过程,并求出答案.
15. 为了测得一棵树的高度 , 一个小组的同学进行了如下测量:在阳光下,测得一根与地面垂直、长为1米的竹竿的影长为0.8米.同时发现这棵树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),测得墙壁上的影长为1.5米,落在地面上的影长为3米.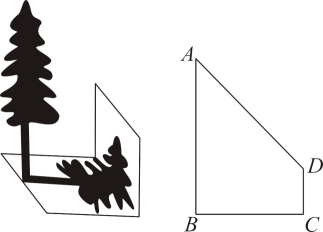 (1)、该小组同学是利用投影的有关知识进行计算的;(填“平行”或“中心”)(2)、求这棵树的高度 .16. 如图,在路灯下,表示小明的身高的线段如AB所示,他在地面上的影子如图中线AC所示,表示小亮的身高的线段如FG所示,路灯灯泡O在线段DE上.
(1)、该小组同学是利用投影的有关知识进行计算的;(填“平行”或“中心”)(2)、求这棵树的高度 .16. 如图,在路灯下,表示小明的身高的线段如AB所示,他在地面上的影子如图中线AC所示,表示小亮的身高的线段如FG所示,路灯灯泡O在线段DE上. (1)、请你确定灯泡O所在的位置,并画出小亮在灯光下形成的影子.(2)、如果小明的身高 , 他的影子长 , 且他到路灯的距离 , 求灯泡的高.17. 为测量水平操场上旗杆的高度,九(2)班各学习小组运用了多种测量方法.
(1)、请你确定灯泡O所在的位置,并画出小亮在灯光下形成的影子.(2)、如果小明的身高 , 他的影子长 , 且他到路灯的距离 , 求灯泡的高.17. 为测量水平操场上旗杆的高度,九(2)班各学习小组运用了多种测量方法. (1)、如图1,小张在测量时发现,自己在操场上的影长恰好等于自己的身高 . 此时,小组同学测得旗杆的影长为 , 据此可得旗杆高度为________m;(2)、如图2,小李站在操场上E点处,前面水平放置镜面C,并通过镜面观测到旗杆顶部A.小组同学测得小李的眼睛距地面高度 , 小李到镜面距离 , 镜面到旗杆的距离 . 求旗杆高度;(3)、小王所在小组采用图3的方法测量,结果误差较大.在更新测量工具,优化测量方法后,测量精度明显提高,研学旅行时,他们利用自制工具,成功测量了江姐故里广场雕塑的高度.方法如下:
(1)、如图1,小张在测量时发现,自己在操场上的影长恰好等于自己的身高 . 此时,小组同学测得旗杆的影长为 , 据此可得旗杆高度为________m;(2)、如图2,小李站在操场上E点处,前面水平放置镜面C,并通过镜面观测到旗杆顶部A.小组同学测得小李的眼睛距地面高度 , 小李到镜面距离 , 镜面到旗杆的距离 . 求旗杆高度;(3)、小王所在小组采用图3的方法测量,结果误差较大.在更新测量工具,优化测量方法后,测量精度明显提高,研学旅行时,他们利用自制工具,成功测量了江姐故里广场雕塑的高度.方法如下:
如图4,在透明的塑料软管内注入适量的水,利用连通器原理,保持管内水面M,N两点始终处于同一水平线上.
如图5,在支架上端P处,用细线系小重物Q,标高线始终垂直于水平地面.
如图6,在江姐故里广场上E点处,同学们用注水管确定与雕塑底部B处于同一水平线的D,G两点,并标记观测视线与标高线交点C,测得标高 , . 将观测点D后移到处,采用同样方法,测得 , . 求雕塑高度(结果精确到).
18. 通常,路灯、台灯、手电筒……发出的光可以看成是从一个点发出的,在点光源的照射下,物体所产生的影称为中心投影.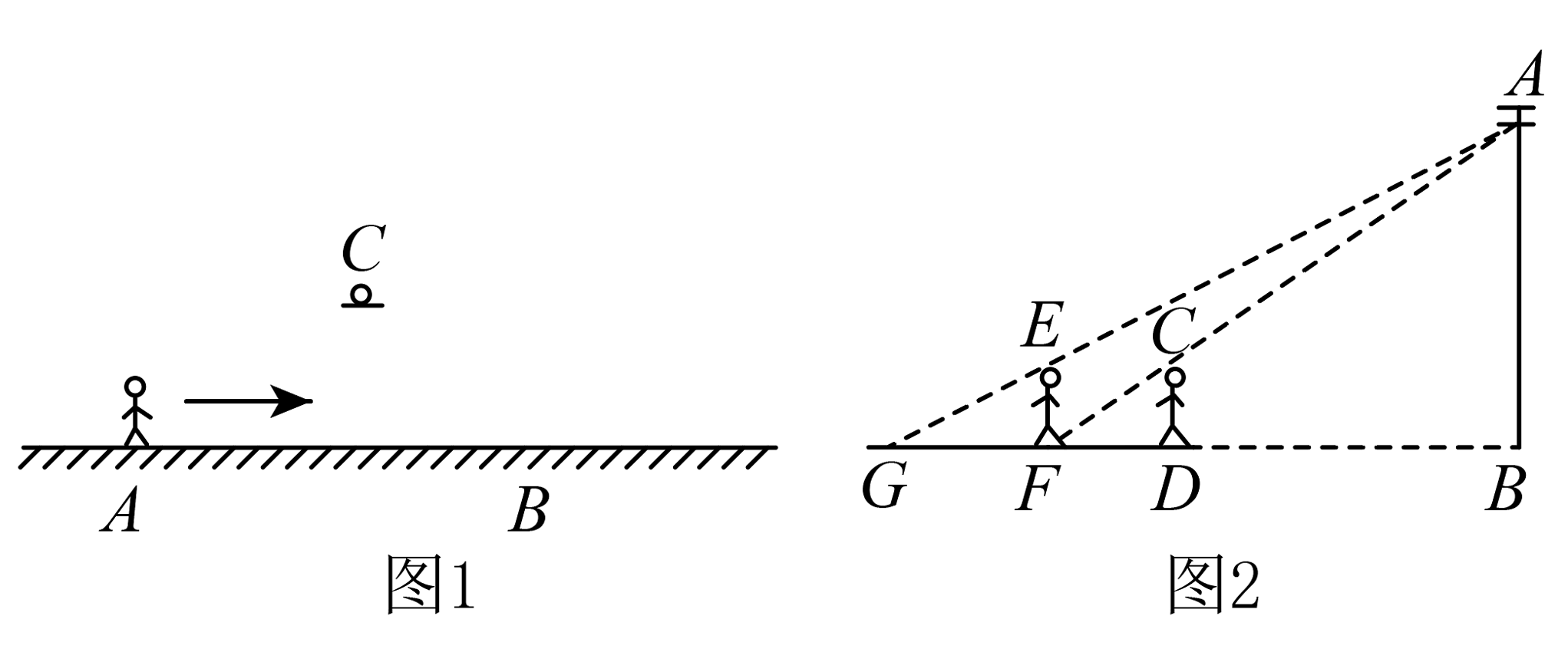 (1)、如图1,夜晚,小明从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间函数关系的图像大致为_________;
(1)、如图1,夜晚,小明从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间函数关系的图像大致为_________;A.
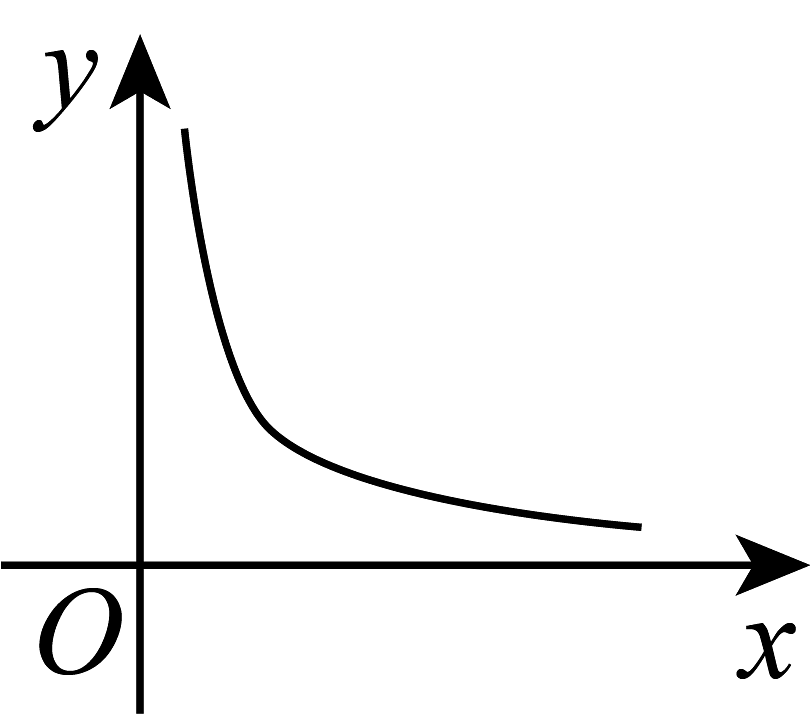 B.
B. 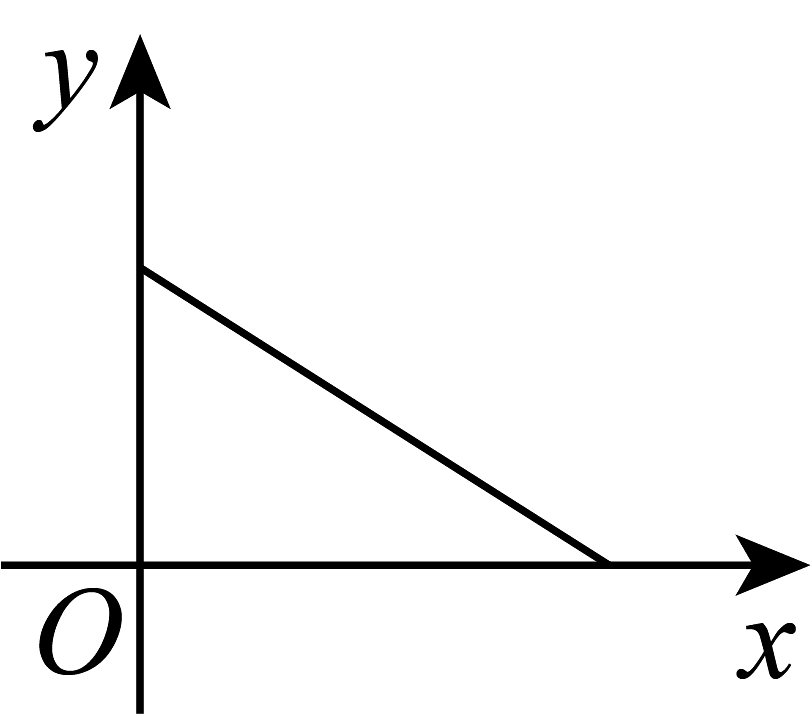 C.
C.  D.
D. 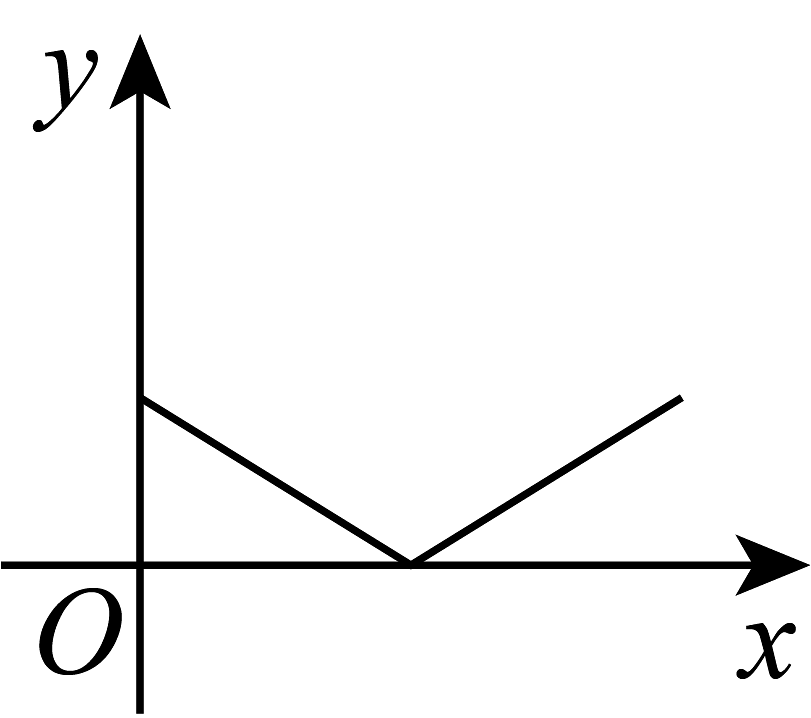 (2)、如图2,小明为测河对岸的路灯杆的高度,在路灯A的灯光下,小明在点D处测得自己的影长 , 沿方向前进到达点F处测得自己的影长 . 已知小明的身高为 , 求路灯杆的高度.19.(1)、从A,B两题中任选一题解答,我选择 .
(2)、如图2,小明为测河对岸的路灯杆的高度,在路灯A的灯光下,小明在点D处测得自己的影长 , 沿方向前进到达点F处测得自己的影长 . 已知小明的身高为 , 求路灯杆的高度.19.(1)、从A,B两题中任选一题解答,我选择 . A、如图(1)是两棵树在同一盏路灯下的影子.①确定该路灯泡所在的位置;②如果此时小颖所在位置恰好与这两棵树所在的位置共线(三点在一条直线上),请画出图中表示小颖影子的线段AB B、如图(2),小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他在某一灯光下的影子为DA,继续按此速度行走2秒到达点F,此时他在同一灯光下的影子落在其身后的线段DF上,测得此时影长MF为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H.他在同一灯光下的影子恰好是HB.图中线段CD,EF,GH表示小明的身高.(2)、请在图中画出小明的影子MF;(3)、若A、B两地相距12米,则小明原来的速度为 .20. 如图
A、如图(1)是两棵树在同一盏路灯下的影子.①确定该路灯泡所在的位置;②如果此时小颖所在位置恰好与这两棵树所在的位置共线(三点在一条直线上),请画出图中表示小颖影子的线段AB B、如图(2),小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他在某一灯光下的影子为DA,继续按此速度行走2秒到达点F,此时他在同一灯光下的影子落在其身后的线段DF上,测得此时影长MF为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H.他在同一灯光下的影子恰好是HB.图中线段CD,EF,GH表示小明的身高.(2)、请在图中画出小明的影子MF;(3)、若A、B两地相距12米,则小明原来的速度为 .20. 如图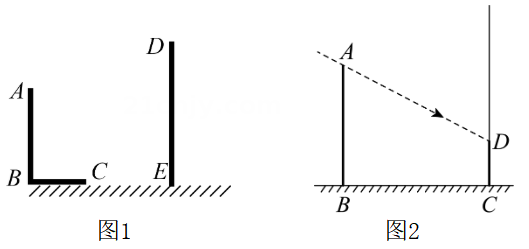 (1)、【基础解答】如图1,AB和DE是直立在地面上的两根立柱,AB=6m,某一时刻AB在阳光下的投影BC=2m,DE在阳光下的投影长为3m.根据题中信息,求立柱DE的长.(2)、【拓展拔高】如图2,古树AB在阳光照射下,影子的一部分照射在地面,即BC=4m,还有一部分影子在建筑物的墙上,墙上的影高CD为1m,同一时刻,竖直于地面上的1m长的竹竿,影长为2m,求这棵古树A8的高.
(1)、【基础解答】如图1,AB和DE是直立在地面上的两根立柱,AB=6m,某一时刻AB在阳光下的投影BC=2m,DE在阳光下的投影长为3m.根据题中信息,求立柱DE的长.(2)、【拓展拔高】如图2,古树AB在阳光照射下,影子的一部分照射在地面,即BC=4m,还有一部分影子在建筑物的墙上,墙上的影高CD为1m,同一时刻,竖直于地面上的1m长的竹竿,影长为2m,求这棵古树A8的高.