6.3 反比例函数的应用-北师大版数学九年级上册

试卷更新日期：2025-11-09 类型：同步测试

进入出卷网下载

一、选择题

1. 三角形的面积为5，底边长为 $x$ ，底边上的高为 $y$ ，则 $y$ 与 $x$ 的函数表达式为（　　）

A、 $y = \frac{10}{x}$ B、 $y = \frac{5}{x}$ C、 $y = \frac{x}{5}$ D、 $y = \frac{x}{10}$

查看试题解析
2. 近似眼镜的度数 $y$ （度）与镜片焦距 $x$ （米）之间具有如图所示的反比例函数关系，若要配制一副度数小于400度的近似眼镜，则镜片焦距 $x$ 的取值范围是（）

A、0米 $< x < 0.25$ 米 B、 $x > 0.25$ 米 C、0米 $< x < 0.2$ 米 D、 $x > 0.2$ 米

查看试题解析
3. 如图所示，学校九年级举行跳绳比赛，图中的四个点分别描述了九年级的四个班级竞赛成绩的优秀率 $y$ （班级优秀人数占班级参加竞赛人数的百分率）与该班参加竞赛人数 $x$ 的情况，其中描述1班和3班两个班级情况的点恰好在同一个反比例函数的图象上，则成绩优秀人数最多的是（）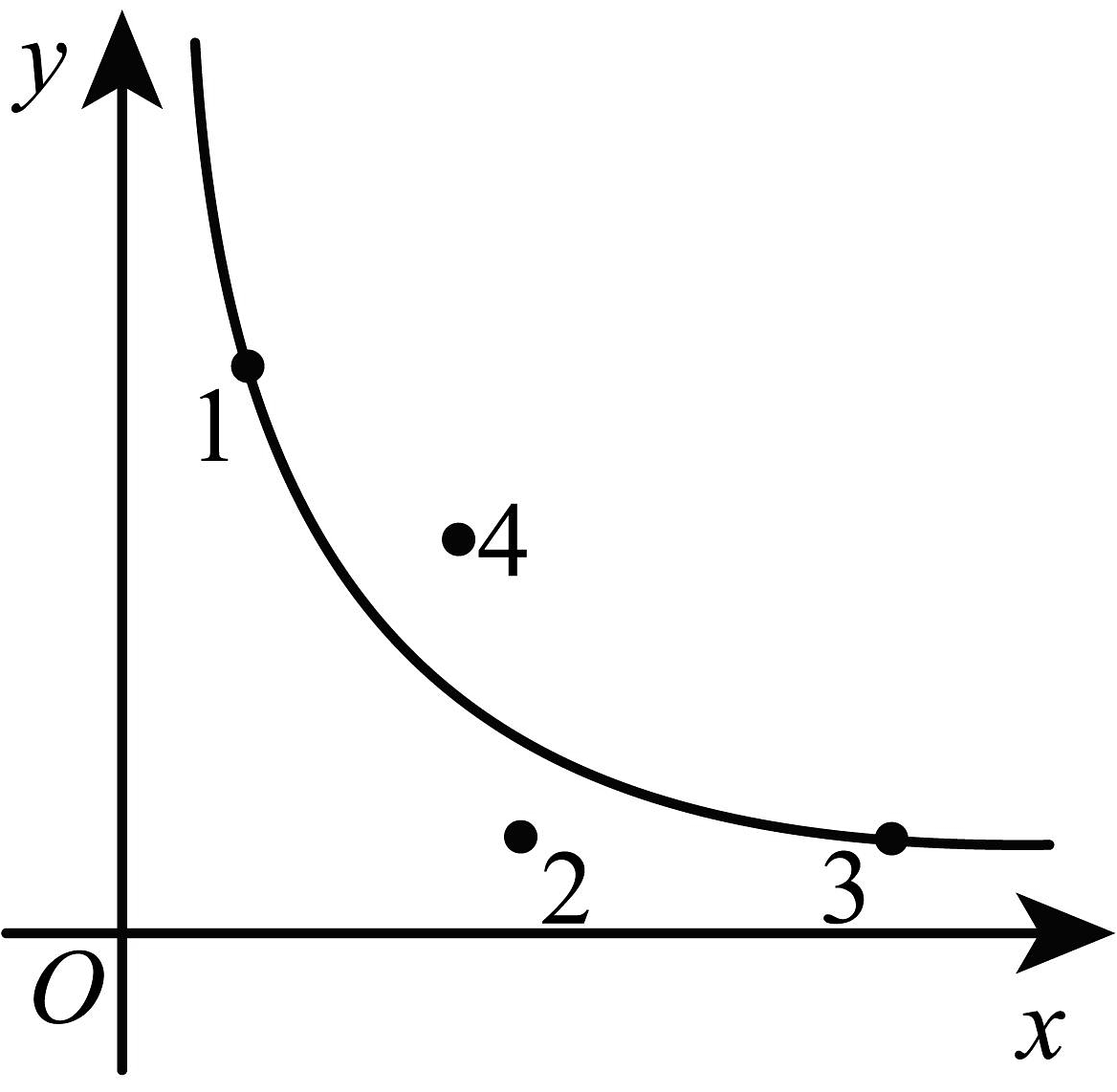

A、1班 B、2班 C、3班 D、4班

查看试题解析
4. 已知蓄电池两端电压U为定值，电流I（单位：A）与电阻R（单位： $Ω$ ）是反比例函数关系，其图象如图所示，下列说法错误的是（）

A、函数表达式为 $I = \frac{24}{R} (R > 0)$ B、在有效范围内，电流I随着电阻R的增大而减小 C、当 $R = 4 Ω$ 时， $I = 12 A$ D、当 $R \geq 3 Ω$ 时， $0 A < I \leq 8 A$

查看试题解析
5. 如图，正比例函数y＝ax（a为常数，且a≠0）和反比例函数y＝ $\frac{k}{x}$ （k为常数，且k≠0）的图象相交于A(﹣2，m)和B两点，则不等式ax＞ $\frac{k}{x}$ 的解集为（　　）

A、x＜﹣2或x＞2 B、﹣2＜x＜2 C、﹣2＜x＜0或x＞2 D、x＜﹣2或0＜x＜2

查看试题解析
6. 在同一直角坐标系中，反比例函数y＝ $\frac{a b}{x}$ 与一次函数y＝ax+b的图象可能是（）

A、 B、 C、 D、

查看试题解析
7. 函数y＝ $\frac{4}{x}$ 和y＝ $\frac{1}{x}$ 在第一象限内的图象如图，点P是y＝ $\frac{4}{x}$ 的图象上一动点，PC⊥x轴于点C，交y＝ $\frac{1}{x}$ 的图象于点B．给出如下结论：①△ODB与△OCA的面积相等；②PA与PB始终相等；③四边形PAOB的面积大小不会发生变化；④CA＝ $\frac{1}{3}$ AP．其中所有正确结论的序号是（）

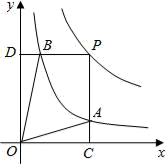A、①②③ B、②③④ C、①③④ D、①②④

查看试题解析
8. 如图，点A在反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象交于A，B两点，点A在第一象限. 点C在x轴正半轴上，连接AC交反比例函数图象于点D. AE为 $∠ B A C$ 的平分线. 过点B作AE的垂线，垂足为E，连接DE. 若 $A C = 3 D C$ ， $△ A D E$ 的面积为 8，则k的值为（）

A、4 B、6 C、8 D、12

查看试题解析

二、填空题

9. 一定质量的氧气，它的密度 $ρ$ （kg/m³）是它的体积 $V$ （m³）的反比例函数，当V＝20m³时， $ρ = 1.36$ kg/m³ ，当V＝40m³时， $ρ =$ kg/m³ ．

查看试题解析
10. 如图，直线 $y_{1} = x - 1$ 与双曲线 $y_{2} = \frac{2}{x}$ 交于点 $A (2, 1)$ ， $B (- 1, - 2)$ ，当 $y_{1} > y_{2}$ 时，则 $x$ 的取值范围是．

查看试题解析
11. 在平面直角坐标系xOy中，对于任意的实数 $a (a \neq 0)$ ，直线 $y = a x + a - 2$ 都经过平面内一个定点 $A$ ．反比例函数 $y = \frac{b}{x}$ 的图象与直线 $y = a x + a - 2$ 交于点 $A$ 和另外一点 $P (m, n)$ ．当 $n > - 2$ 时， $m$ 的取值范围为．

查看试题解析
12. 机器狗是一种模拟真实犬只形态和部分行为的机器装置，其最快移动速度 $v (m/s)$ 是载重后总质量 $m (kg)$ 的反比例函数．已知一款机器狗载重后总质量 $m = 60 kg$ 时，它的最快移动速度 $v = 6 m/s$ ；当其载重后总质量 $m = 90 kg$ 时，它的最快移动速度 $v =$ $m/s$ ．

查看试题解析
13. 如图，点 A，B 分别在反比例函数 $y = \frac{k_{1}}{x} (k_{1} > 0, x > 0)$ ， $y = \frac{k_{2}}{x} (k_{2} < 0, x < 0)$ 的图象上，连结 AB 交 y 轴于点 C，作点 B 关于 x 轴的对称点 D，连结 AD，线段 AD 恰好经过坐标原点 O，若 $\frac{A C}{B C} = \frac{3}{2}$ ，则 $| \frac{k_{1}}{k_{2}} |$ 的值为.

查看试题解析

三、解答题

14. 某工程队修建一条村村通公路，所需天数 $y$ （单位：天）与每天修建该公路长度 $x$ （单位：米）是反比例函数关系，已知该函数关系的图象经过点 $(30, 40)$ ，如图．

(1)、求 $y$ 与 $x$ 之间的函数表达式（不用写出自变量的取值范围）；

(2)、其它条件不变，求该工程队每天修建该公路30米要比每天修建24米提前多少天完成此项工程?

查看试题解析
15. 在坐标系 $x O y$ 中，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象与一次函数 $y = 2 x - 3$ 的图象交点为 $A (n, 1)$ ．

(1)、求反比例函数的解析式；

(2)、当 $1 \leq x < 2$ 时，对于 $x$ 的每一个值，正比例函数 $y = m x$ 的值都小于反比例函数 $y = \frac{k}{x}$ 的值，且大于 $y = \frac{- k}{x}$ 的值，直接写出 $m$ 的取值范围．

查看试题解析
16. 如图，已知反比例函数 $y_{1} = \frac{k}{x}$ （k≠0）的图象与一次函数y₂＝x＋b（b为常数）的图象相交于点A（1，3）．
（1）求这两个函数的表达式及其图象的另一交点B的坐标；
（2）观察图象，写出使函数值y₁＞y₂的自变量x的取值范围；

查看试题解析
17. 我们知道当电压一定时，电流与电阻成反比例函数关系，现有某学生利用一个最大电阻为72欧姆的滑动变阻器及一电流表测电源电压，结果如图所示，当电阻R为12欧姆时，电流I为12安培.

(1)、求电流I（安培）关于电阻R（欧姆）的函数表达式；

(2)、若 $4 \leq R \leq 16$ ，求电流I的变化范围.

查看试题解析
18. 如图，一次函数 $y = k_{1} x + 2$ 的图象与反比例函数 $y = \frac{k_{2}}{x}$ 的图象相交于 $A (m, 4)$ ， $B$ 两点，与 $x$ ， $y$ 轴分别相交于点 $C$ ， $D$ ．且 $tan ∠ A C O = 2$ ．

(1)、分别求这两个函数的表达式；

(2)、以点 $D$ 为圆心，线段 $D B$ 的长为半径作弧与 $x$ 轴正半轴相交于点 $E$ ，连接 $A E$ ， $B E$ ．求 $△ A B E$ 的面积；

(3)、根据函数的图象直接写出关于 $x$ 的不等式 $k_{1} x + 2 > \frac{k_{2}}{x}$ 的解集．

查看试题解析
19. 如图，已知 $A (- 2, - 2), B (n, 4)$ 是一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{m}{x}$ 图象的两个交点，直线 $A B$ 与 $y$ 轴交于点 $C$ ．

(1)、求反比例函数和一次函数的表达式；

(2)、 $M$ 是 $y$ 轴上一点，且 $S_{△ M O B} = S_{△ A O B}$ ，求点 $M$ 的坐标；

(3)、直接写出关于 $x$ 的不等式 $\frac{m}{x} - k x - b > 0$ 的解集．

查看试题解析
20. 小杭在阅读《天工开物》时，看到一种名为桔槔（gāo）的古代汲水工具（如图1），有一横杆固定于桔槔上O点，并可绕O点转动．在横杆A处连接一竹竿，在横杆B处固定300N的物体，且OB＝1m．若图中人物竖直向下的拉力为F，当改变点A与点O的距离l时，横杆始终处于水平状态，小杭记录了拉力的大小F与l的变化，如下表：
点A与点O的距离l/m
1
1.5
2
2.5
3
拉力的大小F/N
300
200
150
120
100

(1)、小杭通过分析表格数据发现， F是l的函数.在如图2所示的平面直角坐标系中，描出表中对应的
点，并画出这个函数的图象；

(2)、根据以上数据和图象，判断F是l的什么函数？直接写出F关于l的函数表达式（不要求写自变量x取值范围）. 并判断当OA的长增大时，拉力F是增大还是减小？请说明理由．

查看试题解析
21. 综合与实践：如何称量一个空矿泉水瓶的重量？
素材1：如图是一架自制天平，支点O固定不变，左侧托盘固定在点A处，右侧托盘的点P可以在横梁BC段滑动.已知OA=OC=12cm ， BC=28cm ，一个100g的砝码.
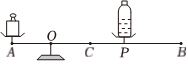
素材2：由于一个空的矿泉水瓶太轻无法称量，小组进行如下操作：左侧托盘放置砝码，右侧托盘滑动点P至点B ，空瓶中加入适量的水使天平平衡，再向瓶中加入等量的水，发现点P移动到PC长12cm时，天平平衡.
链接：根据杠杆原理，平衡时：左盘砝码重量×OA=右盘物体重量×OP.（不计托盘与横梁重量）

(1)、任务1：设右侧托盘放置y（g）物体，OP长x（cm），求y关于x的函数表达式，并求出y的取值范围.

(2)、任务2：求这个空矿泉水瓶的重量.

查看试题解析
22. 如图1，在平面直角坐标系中， $O A = O B = \frac{1}{5} O C = 2$ ，经过A，B两点的直线与反比例函数 $y = \frac{k}{x}$ 在第一象限内的图象交于点D，经过A，C两点的直线与反比例函数 $y = \frac{k}{x}$ 在第一象限内的图象交于点E，已知点D的坐标为（3，5）．

(1)、求直线AC的解析式及E点的坐标；

(2)、若 $y$ 轴上有一动点F，直线AB上有一动点G．当 $E G + \frac{\sqrt{2}}{2} A G$ 最小时，求 $△ E F G$ 周长的最小值；

(3)、如图2，若 $y$ 轴上有一动点Q，直线AB上有一动点 $P$ ，以Q，P，E，D四点为顶点的四边形为平行四边形时，直接写出P点到直线AC的距离．

查看试题解析

点A与点O的距离l/m	1	1.5	2	2.5	3
拉力的大小F/N	300	200	150	120	100