-
1、如图，制作完成后，乐乐握住三角形框架的一部分进行展示，则这个三角形是 （ ）
A、钝角三角形 B、直角三角形 C、锐角三角形 D、以上都有可能 -
2、乐乐截取了三根木棒制作三角形框架，已知其中两根木棒的长度分别为2，5，则第三根木棒截取的长度可以为（ ）A、1 B、3 C、4 D、7
-
3、【教材呈现】下面是人教版八年级上册关于三边关系的一道题目：
填空：
如图①，由三角形两边的和大于第三边，得AB+AD>____，PD+CD> .将不等式左边、右边分别相加，得AB+AD+PD+CD>____，即AB+AC>____.
(1)、补全上面步骤；(2)、【类比猜想】(2)如图②，请你仿照上述解题过程，探究当点 D 与点 P 重合时，AD+BD+CD与 的数量关系，并说明理由. -
4、如图，在一次数学活动中，为了测一堵墙上点A 的高度(AM⊥DM)，小鹿设计了如下方案：
第一步：找一根长度大于AM的直杆，将直杆的一端靠在墙上，且顶端与点 A 重合，记录直杆与地面的夹角∠ABM；
第二步：使直杆顶端沿墙面竖直缓慢下滑，使得∠ =90°-∠____，标记此时直杆的底端点 D；
第三步：测量____的长度，即为点A的高度.
(1)、请你补全小鹿的设计方案；(2)、测得BM=5m，DM=7m，求梯子下滑的高度AC. -
5、如图，在正方形网格中，△ABC 的顶点均在格点上.
(1)、作△ABC 关于直线 l 对称的图形△A'B'C'(点 A，B，C 的对应点分别为点A'，B'，C')；(2)、若网格中小正方形的边长为1，连接BB'，CB'，求△BCB'的面积. -
6、如图， 和 都是等边三角形，且B，C，D三点共线，则有结论：①BE =AD；②∠EBC =∠DAC；③ 请你在①②③中任选一个结论并证明.
-
7、如图，在 中，D 是 AB 上的点，且 求证：△BDC 是等边三角形.
-
8、 西秦刺绣和马勺脸谱是流行于陕西省宝鸡地区的两种特色手工艺品.已知西秦刺绣的单价比马勺脸谱的单价多60 元，小明用1 440元购买西秦刺绣的数量比用1 920 元购买马勺脸谱的数量少8件.某店铺每售出一件西秦刺绣可获得利润30元，每售出一件马勺脸谱可获得利润20元.
(1)、西秦刺绣、马勺脸谱的单价分别是多少元?(2)、该店铺计划初期花费少于 7 200 元的资金购进西秦刺绣、马勺脸谱两种产品共50件，假设这50件产品能够全部卖出，求该店获得销售利润最大的进货方案. -
9、 为巩固拓展脱贫攻坚成果，坚守不发生规模性返贫底线，某脱贫村的农业合作社租用了 14 辆货车，将脱贫户的100 吨大白菜和90 吨平包菜运往农贸市场销售.(1)、已知运平包菜的每辆车的平均载重量是运大白菜的1.2倍，则运大白菜和平包菜的每辆车的平均载重量分别是多少吨?(2)、若这些大白菜第一天销售收入120 000元，第二天每吨的价格比第一天便宜20%，且正好售完，第二天的收入为64 000元，第一天每吨大白菜销售价格是多少元?
-
10、某校开展劳动实践活动，八年级承包了一项劳动任务，1班单独劳动1 小时后，为了加快进度，2班也加入劳动，这样共用3小时完成了任务，已知2班单独劳动需要4小时完成.(1)、1班单独完成此项劳动任务需要多少小时?(2)、若两个班从一开始就合作，需要多少小时完成此项劳动任务?
-
11、北宋科学家沈括的著作《梦溪笔谈》中记载了这样一道问题：军队要为每名士兵配置民夫或骡马来随军运粮.假设为10名士兵配置的民夫可以运粮200石，士兵和民夫每人每天需要吃4升粮.若将民夫换成骡马且数量不变，每匹骡马每天要吃 6 升粮，但运粮的数量增加到500石，且行军天数是原来的2倍.
若随10名士兵行军，需要配置民夫多少人?（注：10升=1斗，10斗=1石)
-
12、科技节期间，学校组织八年级学生乘坐大巴车前往科技馆参观，手机导航推荐了两条路线，如下表所示，设大巴车在路线一中的平均行驶速度为x km/h.
平均行驶速度 km/h
行驶时间/h
全程/ km
路线一
x
80
路线二
1.2x
88
(1)、请用含x的代数式将表格补充完整；(2)、若路线二行驶的时间比路线一用的时间少 h，大巴车在两条路线上行驶时的平均速度分别是多少? -
13、【方法理解】
若x满足（80-x)（x-60)=30，求 的值.
解：设80-x=a，x-60=b，
则（80-x)（x-60)= ab=30，
a+b=（80-x)+（x-60)=20，
【解决问题】(1)、若x满足（30-x)（x-20)=-10，求（30 的值；(2)、如图，正方形ABCD 的边长为x，AE=1，CG=2，长方形 EFGD 的面积是5，四边形 NGDH 和 MEDQ 都是正方形，四边形PQDH 是长方形，求图中阴影部分的面积.（结果必须是一个具体的数值)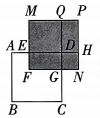
-
14、学校为了让学生进行物理实验的体验和实验效果更好，决定向相关部门申请采购一批新的电流表和电压表.已知市场上电流表的单价比电压表的单价高20%，且学校计划购买电流表和电压表共150台，其中购买电流表花费3 840元，购买电压表花费1600 元.(1)、电压表的单价是多少元?(2)、因原材料市场价格浮动，实验仪器厂商计划对电流表的售价提高20%，电压表的售价为原来的8折，若学校计划再次购进的电流表和电压表的总费用不超过3 800元，且两种仪器共购买100 台，则学校最多可以购买电流表多少台?
-
15、如图，在△ABC中，点 D 在线段 BA 的延长线上，AE平分∠DAC，F为AC 的中点，连接EF并延长交BC 于点 G，且AE∥BC.
(1)、在证明△ABC是等腰三角形时，小新同学的证明过程如下，请你将过程和依据补充完整；证明：∵AE∥BC，
∴∠B=∠DAE，（ )
∠C= ▲ ， （两直线平行，内错角相等)
∵AE平分∠DAC，
∴∠DAE=∠CAE，
∴∠B=∠C，
∴AB=AC，（ )
∴△ABC 是等腰三角形.
(2)、若AE=8，AB=10，GC=2BG，求△ABC的周长. -
16、如图，在平面直角坐标系中，△ABC 的三个顶点坐标分别是A（-2，3)，B（-4，-1)，C（3，2).
(1)、作△ABC 关于y轴对称的△A'B'C'，并写出顶点A'，B'，C'的坐标；(2)、在x轴上标出点 M，使得AM+CM 的值最小. -
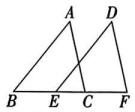
17、如图，在△ABC 和△DEF中，B，E，C，F在同一条直线上，AB=DE，AB∥DE，BE=CF，求证：△ABC≌△DEF.
-
18、已知关于x的不等式组 至少有三个整数解，且关于y 的分式方程 的解为非负数，写出所有满足条件的整数a的值.
-
19、若分式方程 的解为非负数，求k的取值范围.
-
20、不等式4x+3>3x-2的最小整数解是分式方程 的解，求k的值.