相关试卷

1、如图，已知△ABC≌△EDF，若BC=4，D为BC的中点，则CF的长为 ( )

A、1 B、1.5 C、2 D、2.5

查看解析
2、如图是两个全等三角形，字母a，b，c分别表示三角形的边长，根据图中数据，则∠1 的度数为( )

A、55° B、60° C、65° D、66°

查看解析
3、谷纹环是战国中期的玉器，如图是战国谷纹环的平面示意图，下列图形中与该示意图全等的是 ( )

A、 B、 C、 D、

查看解析
4、我们把多项式 $a^{2} \pm 2 a b + b^{2}$ 叫作完全平方式.如果一个多项式不是完全平方式，我们常对其变形使之成为一个完全平方式，如先添加一个适当的项，使式子出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法.即把一个非完全平方式的多项式，通过变形成为一个完全平方式与一个单项式的和.这种方法是数学中一种重要的解题方法.通过这样的变形，可以解决数学中代数式的最大值、最小值的问题.
例：求代数式 $x^{2} + 2 x$ 的最小值.通过变形得到 $x^{2} + 2 x = x^{2} + 2 x + 1 - 1$
$= {(x + 1)}^{2} - 1,$
$∵ {(x + 1)}^{2}$ 是非负数，
$∴ {(x + 1)}^{2} \geq 0,$
$∴ {(x + 1)}^{2} - 1 ⩾ - 1,$
$∴ x^{2} + 2 x$ 的最小值为-1.
阅读上面的材料，回答下列问题：

(1)、填空： $a^{2} + 6 a = a^{2} + 6 a$ +-=²-

(2)、求多项式 $m^{2} + 16 m$ 的最小值；

(3)、多项式 $- 4 m^{2} + 60 m + 2$ 是否存在最值?若存在，求出最值；若不存在，请说明理由.

查看解析
5、如图，AE=BE，CE=DE，点D 在AC边上， $∠ D E C = ∠ B E A,$ AE 和 BD 相交于点O.

(1)、求证： $△ A E C ≅ △ B E D;$

(2)、若 $∠ D E C = 4 0^{\circ},$ 求 $∠ B D E$ 的度数.

查看解析

6、阅读下面材料：

在数学课上，老师提出了如下问题：如图，在△ABC中，AB<BC，用尺规作图法在 BC 上取一点 P，使得PA+PC=BC.

小明的作法及证明过程如下：

（1）作线段AB的垂直平分线l，

（2）直线l交 BC 于点 P，则点 P 就是所求的点.

证明：连接PA，

∵直线l垂直平分线段AB，

∴PA=PB（依据：____)，

∵BC=PB+PC，

∴ PA+PC=BC.

老师说：“小明的作法和证明过程完全正确.”

解决下列问题：

(1)、利用尺规作图确定点 P 的位置；（保留作图痕迹，不写作法)

(2)、补全证明过程中的依据.

查看解析

7、夏季室内闷热，空气循环扇配合空调使用，可让室温均衡，达到快速制冷的效果.某商场计划购进某工厂的空气循环扇，第一次用8 000 元购进一批空气循环扇，销售完后，第二次又用17 600 元购进一批同款空气循环扇，数量是第一次购进数量的2倍，但单价贵了 10 元.该商场第一次购进多少台空气循环扇?

查看解析
8、如图，在△ABC中，AB=AC，CD，BE是△ABC 两腰上的高，CD，BE 交于点 F.求证：△BCF 是等腰三角形.

查看解析
9、如图①，用一根细绳从质地均匀的三角形薄板的重心处穿过，并将其悬挂在支架上，观察发现三角形薄板正好保持水平，数学兴趣小组对产生这一现象的原因进行了探究.请你帮助他们完成下列问题：

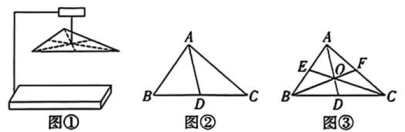(1)、如图②，小组成员在三角形薄板ABC 上画出中线AD，可以得到 $S_{△ A B D}$ $S_{△ A C D}$ （填“>”“=”或“<”）；

(2)、如图③，三角形薄板ABC的三条中线AD，CE，BF相交于点O，试判断三角形薄板ABC 被三条中线所分成的六个小三角形的面积之间的数量关系，并说明理由；

(3)、结合（2）中的结论，试猜想AO：OD，BO：OF，CO：OE 的值，并说明理由.

查看解析
10、如图①，兔子在第一次龟兔赛跑失利后，不服输的它又组织了一次比赛，这次的比赛规则是从点A 跑到点 B，但A，B之间设置了很多陷阱，兔子选择沿路线A→C→B 前进，乌龟可以选择的路线分别是：路线①A→C→B；路线②A→E→F→B；路线③A→D→B.

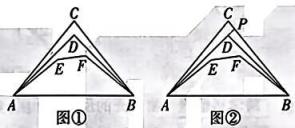(1)、若乌龟选择了路线③，那么乌龟和兔子的路线哪个更短呢?请说明理由.
以下是小明不完整分析过程，请你帮他补充完整；
解：乌龟的路线更短，理由如下：
如图②，延长AD交 BC 于点 P，
在 $△ A P C$ 中，AC+CP>AP，
$∴ A C + C P > A D + D P,$
…

(2)、请你帮乌龟从路线②和③中选择一条较短的路线，并说明理由.

查看解析
11、如图，是由线段组成的图案，其中线段AF，BE，CD 相交于点P，连接EF，AD，BC，若. $∠ E P F = 6 0^{\circ},$ 求 $∠ A + ∠ B + ∠ C + ∠ D +$ $∠ E + ∠ F$ 的度数.

查看解析
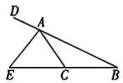
12、如图，已知 $△ A B C,$ ，延长BA至点D，AE平分. $∠ C A D$ 交BC的延长线于点 E.求证： $∠ A C B = ∠ B + 2 ∠ E .$

查看解析
13、如图，在 $△ A B C$ 中，AD是 $△ A B C$ 的角平分线.

(1)、画出BC边上的高AE；

(2)、在（1）的条件下，若 $∠ B = 2 8^{\circ}, ∠ B C A = 12 0^{\circ},$ 求 $∠ C A D$ 的度数.

查看解析
14、已知等腰三角形的两边a，b满足 ${(a - 7)}^{2} + ∣ b - 15 ∣ = 0,$ 求这个等腰三角形的周长.

查看解析
15、已知：如图， $∠ A C D$ 是 $△ A B C$ 的外角.求证： $∠ A + ∠ B = ∠ A C D .$ 请将以下证明过程补充完整：
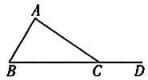
证明：∵ $∠ A + ∠ A C B + ∠ B = 18 0^{\circ}$
▲ + ▲ $= 18 0^{\circ}$
∴ ▲

查看解析
16、现有四根长分别为3cm，5cm，7cm，x cm（x为正整数）的木棒，从中任取三根木棒组成三角形，若组成三角形的周长为18cm，则x的值为

查看解析
17、如图，位于A处的一艘军舰观测到一艘巡逻艇B在其南偏西60°的方向上，巡逻艇C在其南偏东 $2 0^{\circ}$ 方向上，已知 $∠ C B E = 8 0^{\circ},$ ，则∠C的度数为.

查看解析
18、如图，BD是△ABC的中线，AB=3，BC=5，△ABD 的周长为9，则△BCD 的周长为

查看解析
19、如图所示的图形中，共有个三角形.

查看解析
20、一个三角形的三个内角的度数如图所示，则x的值为.

查看解析

上一页 84 85 86 87 88 下一页跳转