相关试卷
-
1、下列各图象中,不能表示y是x的函数的是( )A、
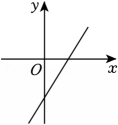 B、
B、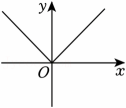 C、
C、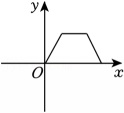 D、
D、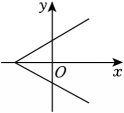
-
2、如图1,四边形ABCD是平行四边形,延长AB至点E,使得BE=AB,连接BD和CE.
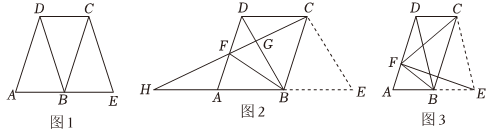 (1)、求证:四边形BECD是平行四边形;(2)、如图2,将△CBE沿直线BC翻折,点E刚好落在AD的中点F处,延长CF与BA的延长线交于点H,并且CF和BD交于点G,试探究线段CH、FG、GB之间的数量关系;(3)、如图3,将△CBE沿直线BC翻折,点E刚好落在AD的点F处,若AD=6,DC=3,且FD=2FA,求的面积.
(1)、求证:四边形BECD是平行四边形;(2)、如图2,将△CBE沿直线BC翻折,点E刚好落在AD的中点F处,延长CF与BA的延长线交于点H,并且CF和BD交于点G,试探究线段CH、FG、GB之间的数量关系;(3)、如图3,将△CBE沿直线BC翻折,点E刚好落在AD的点F处,若AD=6,DC=3,且FD=2FA,求的面积. -
3、2025年春晚舞台上,宇树科技的人形机器人以一身喜庆的大红棉袄亮相,随着秧歌舞步灵活扭动,手中的红手绢在空中划出流畅弧线.这场表演不仅让观众惊叹于机器人动作的精准协调,更因“机器人舞团”在舞蹈时队形变化整齐无误,成为社交媒体热议的焦点.某公司计划购买A、B两种机器人进行销售.已知每个B种机器人比种机器人贵5万元,用1200万元购进A种机器人的数量是用650万元购进B种机器人数量的2倍.(1)、求购买一个种机器人、一个B种机器人各需多少万元?(2)、一段时间后,该公司准备用不超过6200万元再购进第二批A、B两种机器人共100个,且A种机器人数量不超过B种机器人数量的3倍.据市场销售分析,当A种机器人提价15%,B种机器售价为购买价的倍时,销售状况最好,若按此销售方案将第二批机器人全部销售完,怎样安排购进方案可以使获得的利润最大,求出最大利润及对应的购进方案.
-
4、 如果关于某一字母的二次多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式的最大值、最小值等.
例如:分解因式x2+2x﹣3.
原式=(x2+2x+1)﹣4=(x+1)2﹣4=(x+1+2)(x+1﹣2)=(x+3)(x﹣1).
例如:求代数式x2+4x+6的最小值.
原式=x2+4x+4+2=(x+2)2+2.∵(x+2)2≥0,∴当x=﹣2时,x2+4x+6有最小值,最小值是2.
根据阅读材料用配方法解决下列问题:
(1)、分解因式:m2﹣4m﹣5= 求代数式x2﹣6x+12的最小值为 ;(2)、若y=﹣x2+2x﹣3,当x= 时,y有最 值(填“大”或“小”),这个值是 ;(3)、当a , b , c分别为△ABC的三边长,且满足a2+b2+c2﹣6a﹣10b﹣6c+43=0时,求△ABC的周长。 -
5、 如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边在AB上方作等边△ABD , 点F是线段AD的中点,连接CF .
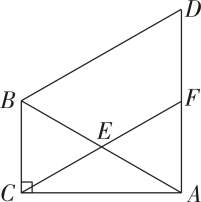 (1)、若AC=3,求AD的长;(2)、求证:四边形BCFD是平行四边形.
(1)、若AC=3,求AD的长;(2)、求证:四边形BCFD是平行四边形. -
6、如图,等腰三角形ABD中,AB=AC.
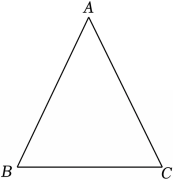 (1)、在线段AC上求作点D,使得点D到AB和BC的距离相等(要求:尺规作图,不写作法,保留作图痕迹);(2)、在(1)所作的图形中,连接 , 若AD=BD,求∠A的度数.
(1)、在线段AC上求作点D,使得点D到AB和BC的距离相等(要求:尺规作图,不写作法,保留作图痕迹);(2)、在(1)所作的图形中,连接 , 若AD=BD,求∠A的度数. -
7、 如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).

⑴画出△ABC关于原点O的中心对称图形△A1B1C1;
⑵将△ABC绕原点O顺时针旋转90°后得到△A2B2C2 , 请画出△A2B2C2 .
-
8、先化简,再求值: , 其中 .
-
9、解不等式组 , 并把解集在数轴上表示出来.
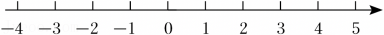
-
10、 如图,将等边三角形ABC沿射线BC向右平移一定的距离得到△DEF.若AB=2,EC=2BE,则图中阴影部分的面积为 .
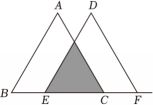
-
11、 一个多边形的每个内角都是108°,那么这个多边形是 .
-
12、分解因式:18-2m2=.
-
13、 数形结合是解决数学问题常用的思想方法.如图,一次函数y=kx+b(k、b为常数,且k<0)的图象与直线y=x都经过点A(3,1),当kx+b<x时,x的取值范围是( )
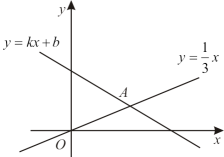 A、x>3 B、x<3 C、x<1 D、x>1
A、x>3 B、x<3 C、x<1 D、x>1 -
14、关于x的分式方程无解,则m的值为( )A、3 B、2 C、-3 D、-2
-
15、 如图,在△ABC中,AB边上的垂直平分线分别交边AC于点E , 交边AB于点D , 若AC的长为9cm,的长为6cm,则EC的长为( )
 A、2cm B、3cm C、4cm D、5cm
A、2cm B、3cm C、4cm D、5cm -
16、 若关于x的不等式组的解集为x<3,则m的取值范围是( )A、m≥3 B、m≤3 C、m≥1 D、m≤1
-
17、在平面直角坐标系中,若点N(x , y)的坐标满足2x+y=3,则我们称点N为“健康点”;若点Q(x , y)的坐标满足x﹣2y=﹣1,则我们称Q为“快乐点”。
 (1)、若点A(a , b)既是“健康点”又是“快乐点”,则点A的坐标为 ;(2)、在(1)的条件下,若点B是x轴上的“快乐点”,点C是y轴上的“健康点”,如果P为x轴上一点,且三角形BPC是三角形ABC面积的3倍,求点P的坐标;(3)、在上述条件下,直线AB与x轴所夹的锐角为α,直线AC与y轴所夹的锐角为β,试探究∠BAC与α和β之间的数量关系,并说明理由.
(1)、若点A(a , b)既是“健康点”又是“快乐点”,则点A的坐标为 ;(2)、在(1)的条件下,若点B是x轴上的“快乐点”,点C是y轴上的“健康点”,如果P为x轴上一点,且三角形BPC是三角形ABC面积的3倍,求点P的坐标;(3)、在上述条件下,直线AB与x轴所夹的锐角为α,直线AC与y轴所夹的锐角为β,试探究∠BAC与α和β之间的数量关系,并说明理由. -
18、定义运算:f(x , y)=ax+by . 已知f(3,2)=7,f(4,3)=10.(1)、直接写出:a= ,b= ;(2)、若关于x的不等式组无解,求t的取值范围;(3)、若f(mx+3n , 2m﹣nx)≥3m+4n的解集为 , 求不等式:f(mx﹣2m , 3n﹣nx)>﹣m+n的解集.
-
19、2025年国家卫健委建议实施“体重管理年”三年行动某校要组织学生外出研学,根据营养师的建议准备了A,B两种食品作为午餐A餐每包的热量为700千焦,蛋白质为5克.B餐每包热量为800千焦,蛋白质为10克。(1)、若要从这两种食品中摄入3700千焦热量和35克蛋白质,应选用A,B两种食品各多少包?(2)、运动量大的人或青少年对蛋白质的摄入量应更多.若每份午餐选用这两种食品共7包,要使每份午餐中的蛋白质含量不低于55克,且热量最低,应如何选用这两种食品?
-
20、补全下面推理过程:
生活中常见的一种折叠拦道闸,如图①所示.若想求解某些特殊状态下的角度,需将其抽象为几何图形,如图②所示,BA垂直于地面AE于点A,CD平行于地面AE,求∠ABC+∠BCD的度数。

解:如图②,过点B作BF//AE.
∵CD∥AE ( ) ,
∴ ∥ CD (平行于同一条直线的两条直线平行),
∴∠BCD+ = 180°( )
∵AB⊥AE,
∴∠EAB= ( )
∵BF∥AE(辅助线作法),
∴ +∠EAB=180°,
∴∠ABF=180°—∠EAB= ,
∴∠ABC+∠BCD=∠ABF+∠CBF+∠BCD=