冀教版数学八年级上学期期中仿真模拟试卷一（范围：12-14章）

试卷更新日期：2025-09-21 类型：期中考试

进入出卷网下载

一、选择题：本大题共12小题，每小题3分，共36分.在每小题给出的四个选项中，只有一个是正确的.每小题选对得3分，选错、不选或多选，均不得分.

1. 下列命题的逆命题是真命题的是（）

A、全等三角形的对应角相等 B、如果两个有理数相等，那么它们的平方相等 C、如果两个角是对顶角，那么这两个角相等 D、两直线平行，同位角相等

查看试题解析
2. 据人民网消息，2024年国庆假期，我国国内旅游出游约7.65亿人次．其中近似数“7.65亿”精确到的数位是（）

A、百分位 B、十分位 C、千万位 D、百万位

查看试题解析
3. 若分式 $\frac{m}{m - 2}$ 有意义，则m满足的条件是（）

A、 $m \neq 2$ B、 $m > 2$ C、 $m \neq 0$ D、 $m < 2$

查看试题解析
4. 如图是两个全等三角形，图中的字母表示三角形的边长，则 $∠ 1$ 的度数是（）

A、 $115 °$ B、 $65 °$ C、 $40 °$ D、 $25 °$

查看试题解析
5. 将分式 $\frac{x^{2}}{x + y}$ 中的x，y的值同时扩大到原来的3倍，则分式的值（）

A、扩大到原来的3倍 B、缩小到原来的 $\frac{1}{3}$ C、保持不变 D、无法确定

查看试题解析
6. 下列各式中正确的是（）

A、 $\sqrt{9} = \pm 3$ B、 $\sqrt[3]{- 27} = - 3$ C、 $\pm \sqrt{16} = 4$ D、 $\sqrt{(- 2)^{2}} = - 2$

查看试题解析
7. 实数 $1 - 3 a$ 有平方根，则 $a$ 可以取的值为（）

A、0 B、1 C、2 D、3

查看试题解析
8. 如图，在综合实践课上，老师用角尺在∠AOB的两边分别截取OM=ON，移动角尺，使角尺两边相同的刻度分别与点 M，N重合，这时OC 就是∠AOB 的平分线，则用角尺作角平分线的过程中用到的三角形全等的依据是（）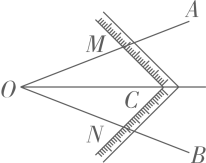

A、HL B、SSS C、SAS D、ASA

查看试题解析
9. 已知 $\frac{x^{2} - 4}{x - 3} \div \frac{▲}{x^{2} - 9}$ ，这是一道分式化简题，因为一不小心一部分被墨水污染了，若只知道该题化简的结果为整式，则被墨水覆盖的部分不可能是（）

A、 $x - 3$ B、 $x - 2$ C、 $x + 3$ D、 $x + 2$

查看试题解析
10. 实数 $\sqrt{5} + 1$ 在数轴上的对应点可能是（　　）

A、点P B、点Q C、点M D、点N

查看试题解析
11. 如图，小明做了一个长方形框架，发现很容易变形，请你帮他选择一个最好的加固方案(　　)

A、 B、 C、 D、

查看试题解析
12. 如图，在 $∠ B A C$ 的两边上截取 $A B = A C$ ， $A D = A E$ ．连接 $B D$ ， $E C$ 交于点 $P$ ，则下列结论正确的是 $($ 　　 $)$
① $Δ A B D ≅ Δ A C E$ ；② $Δ B E P ≅ Δ C D P$ ；③ $Δ A P B ≅ Δ A P C$ ；④ $Δ A P E ≅ Δ A P D$ ．

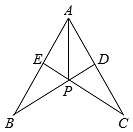A、①②③④ B、①②③ C、②③④ D、①③④

查看试题解析

二、填空题：本大题共4小题，每小题4分，共16分.

13. 写出命题“两个全等三角形的周长相等”的逆命题．

查看试题解析
14. 如图是一个电脑运算程序图，当输入不相等的 $a$ ， $b$ 后，按照程序图运行，会输出一个结果．若 $a = 5$ ， $b = x$ 时，输出的结果为2，则 $x$ 的值为．

查看试题解析
15. 已知 $1 1^{3} = 1331 ， 1 2^{3} = 1728 ， 1 3^{3} = 2197 ， 1 4^{3} = 2744$ ．若 $n$ 为整数，且 $n < \sqrt[3]{2023} < n + 1$ 则 $n =$ ．

查看试题解析
16. 如图，在四边形 $A B C D$ 中， $A B = A D$ ， $∠ B A D = 140^{\circ}$ ， $A B ⊥ C B$ 于点 $B$ ， $A D ⊥ C D$ 于点 $D$ ， $E$ ， $F$ 分别是 $C B$ ， $C D$ 上的任意一点，且 $∠ E A F = 70^{\circ}$ ，下列说法： $① D F = B E$ ； $② △ A D F ≌ △ A B E$ ； $③ F A$ 平分 $∠ D F E$ ； $④ A E$ 平分 $∠ F A B$ ； $⑤ B E + D F = E F$ ； $⑥ C F + C E > F D + E B$ .其中正确的是.（填写正确的序号）

查看试题解析

三、解答题：本大题8小题，共72分.

17. 计算：

(1)、 $\frac{2 a}{a + 4} \cdot \frac{a^{2} + 8 a + 16}{4 a^{2}}$ ；

(2)、 $(x^{2} - 2 x) \div \frac{x - 2}{2 x}$ ．

查看试题解析
18. 先化简，再求值： $(1 - \frac{1}{x - 1}) \div \frac{x^{2} - 4 x + 4}{x^{2} - 1}$ ，从 $- 1$ ，1，2，3中选择一个合适的数代入并求值.

查看试题解析
19. 义务献血利国利民，是每个健康公民应尽的义务。一个采血点通常在规定时间接受献血，采血结束后，再统一送到市中心血库，且采血和送到血库的时间必须在4小时内完成，超过4小时送达，血液将变质. 已知A、 B两个采血点到中心血库的路程分别为30km、36km，经过了解获得A、B两个采血点的运送车辆有如下信息：
信息一： B采血点运送车辆的平均速度是A采血点运送车辆的平均速度1.2倍；
信息二：A、B两个采血点运送车辆行驶的时间之和为2小时.

(1)、求A、B两个采血点运送车辆的平均速度各是多少?

(2)、若B采血点完成采血的时间为2.5小时，判断血液运送到中心血库后会不会变质?

查看试题解析
20. 在数学课上，林老师在黑板上画出如图所示的图形(其中点B，F，C，E在同一直线上)，并写出四个条件：①AB=DE，②BF=EC，③∠B=∠E，④∠1=∠2.
请你从这四个条件中选出三个作为已知条件，另一个作为结论，组成一个真命题，并给予证明.
已知条件：.
结论：(均填写序号).
证明：

查看试题解析
21. 阅读理解，观察下列式子：
① $\sqrt[3]{8} + \sqrt[3]{- 8} = 2 + (- 2) = 0$ ；
② $\sqrt[3]{1} + \sqrt[3]{- 1} = 1 + (- 1) = 0$ ；
③ $\sqrt[3]{1000} + \sqrt[3]{- 1000} = 10 + (- 10) = 0$ ；
$\sqrt[\begin{array}{l} 3 \end{array}]{\frac{1}{27}} + \sqrt[\begin{array}{l} 3 \end{array}]{- \frac{1}{27}} = \frac{1}{3} + (- \frac{1}{3}) = 0$ ；
…
根据上述等式反映的规律，回答如下问题：

(1)、根据以上式子的规律，写出一个类似的等式：______．

(2)、由等式①，②，③，④所反映的规律，可归纳为一个这样的真命题：对于任意两个有理数 $a$ ， $b$ ，若______，则 $\sqrt[3]{a} + \sqrt[3]{b} = 0$ ；反之也成立．

(3)、根据上述的真命题，解答问题：若 $\sqrt[3]{3 - 2 x}$ 与 $\sqrt[3]{x + 5}$ 的值互为相反数，求 $x$ 的值．

查看试题解析
22. 综合与实践：
【问题情境】如图所示，池塘的两端有A，B两点，现需要测量该池塘的两端A，B之间的距离，需要如何进行呢？
【提出方案】同学们想出了如下的两种方案：
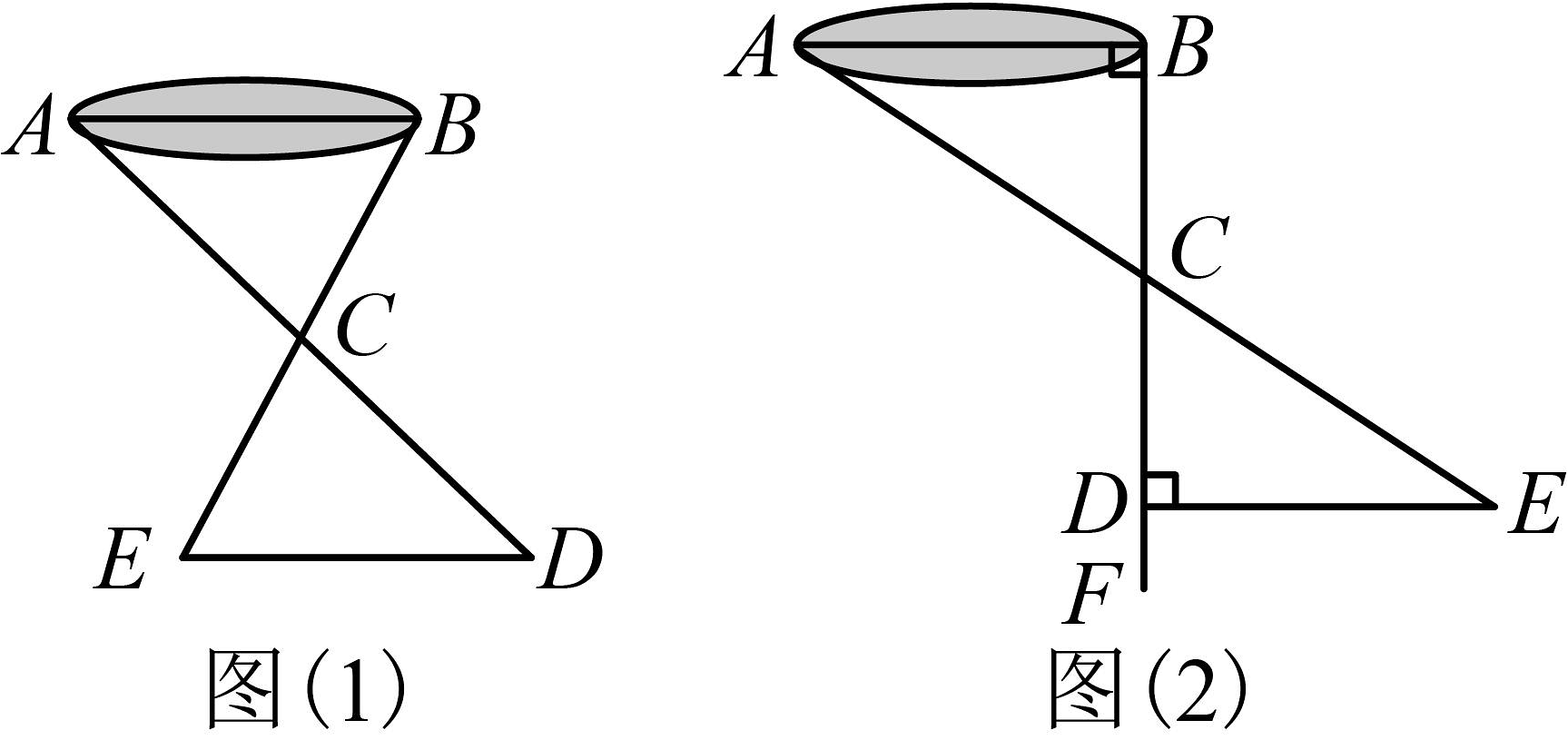
甲同学：如图（1）所示，先在平地上取一个可直接到达A，B的点C，再连接 $A C ， B C$ ，并分别延长 $A C$ 至点D， $B C$ 至点E，使 $D C = A C$ ， $E C = B C$ ，最后量出 $D E$ 的距离就是 $A B$ 的距离；
乙同学：如图（2）所示，过点B作 $A B$ 的垂线 $B F$ ，在 $B F$ 上取C，D两点，使 $B C = C D$ ，接着过点D作 $B D$ 的垂线 $D E$ ，在垂线上选一点E，使A，C，E三点在一条直线上，则测出 $D E$ 的长即是 $A B$ 的距离．
【问题解决】请你选择一位同学的方案，判断其是否可行，并说明理由．

查看试题解析

23. 八年级数学兴趣小组开展了测量学校教学楼高度

A B

的实践活动，测量方案如下表：

课题	测量学校教学楼高度 $A B$
测量工具	测角仪、皮尺等
测量方案示意图
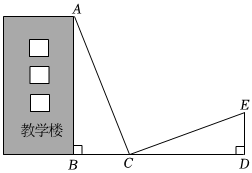
测量步骤	$(1)$ 在教学楼外，选定一点 $C$ ； $(2)$ 测量教学楼顶点 $A$ 视线 $A C$ 与地面夹角 $∠ A C B$ ； $(3)$ 测 $B C$ 的长度； $(4)$ 放置一根与 $B C$ 长度相同的标杆 $D E$ ， $D E$ 垂直于地面； $(5)$ 测量标杆顶部 $E$ 视线与地面夹角 $∠ E C D$ ．
测量数据	$∠ A C B = 68.2 °$ ， $∠ E C D = 21.8 °$ ， $B C = D E = 2.5 m$ ， $C D = 12 m$

请你根据兴趣小组测量方案及数据，计算教学楼高度 $A B$ 的值．

查看试题解析

24. 综合与探究：问题情景：如图 $1$ 所示，已知，在 $△ A B C$ 中， $A C = B C$ ， $∠ A C B = 90 °$ ， $A D$ 是 $△ A B C$ 的中线，过点 $C$ 作 $C E ⊥ A D$ ，垂足为 $M$ ，且交 $A B$ 于点 $E$ ．

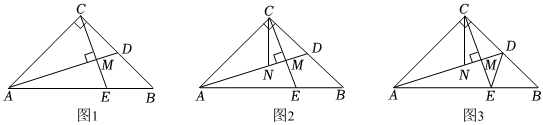(1)、 $($ 探究一 $)$ 小虎通过度量发现 $∠ B C E = ∠ C A D$ ，请你帮他说明理由；

(2)、 $($ 探究二 $)$ 小明在图中添加了一条线段 $C N$ ，且 $C N$ 平分 $∠ A C B$ 交 $A D$ 于点 $N$ ，如图 $2$ 所示，即可得 $C N = B E$ ，符合题意吗？请说明理由；

(3)、 $($ 探究三 $)$ 小刚在 $(2)$ 的基础上，连接 $D E$ ，如图 $3$ 所示，若 $A B = 4$ ， $C N = \frac{4}{3}$ ，求 $△ A D E$ 的面积．

查看试题解析