第四章《一元一次方程》提升卷—苏科版数学七(上)单元测
试卷更新日期:2025-09-21 类型:单元试卷
一、选择题:本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一个是正确的.每小题选对得3分,选错、不选或多选,均不得分.
-
1. 如果甲、乙、丙三个村合修一段水渠,计划出工65人,按各村受益土地面积3:4:6出工,求各村应出工的人数. ①设甲、乙、丙三村分别派3x,4x,6x人,依题意可得3x+4x+6x=65; ②设甲村派x人,依题意得x+4x+6x=65; ③设甲村派x人,依题意得x+x+2x=65; ④设丙村派x人,依题意得3x+4x+x=65.上面所列方程中正确的是( )A、①② B、②③ C、③④ D、①③2. 有下列各式:①4+8=12;②5y+8;③2x2+x=1;④2x2-5x-1;⑤|x|+1=2; 6y-9。其中属于方程的是( )A、①③⑤ B、②④ C、③⑤⑥ D、①④⑥3. 若不论 取什么实数,关于 的方程 ( 、 常数)的解总是 ,则 的值是( )A、 B、 C、 D、4. 已知m,n都是质数,若关于x的方程 mx+5n=97的解为3,则 ( )A、0 B、3 C、5 D、135. 设■,●,▲分别表示三种不同的物体,如图所示,前两架天平保持平衡,如果要使第三架天平也保持平衡,那么第三架天平右边不能放的是( )
 A、▲▲▲▲ B、▲▲▲▲▲ C、●●▲ D、●▲▲▲6. 我国古代的“河图”是由的方格构成的,每个方格内均有.数目(个数为1~9)不同的点图,用实心点“●”表示正数,空心点“○”表示负数.每一行、每一列以及每一条对角线上的三个点图的点数之和均相等.如图,给出了“河图”的部分点图,请你推算出P处所对应的点图是( )
A、▲▲▲▲ B、▲▲▲▲▲ C、●●▲ D、●▲▲▲6. 我国古代的“河图”是由的方格构成的,每个方格内均有.数目(个数为1~9)不同的点图,用实心点“●”表示正数,空心点“○”表示负数.每一行、每一列以及每一条对角线上的三个点图的点数之和均相等.如图,给出了“河图”的部分点图,请你推算出P处所对应的点图是( )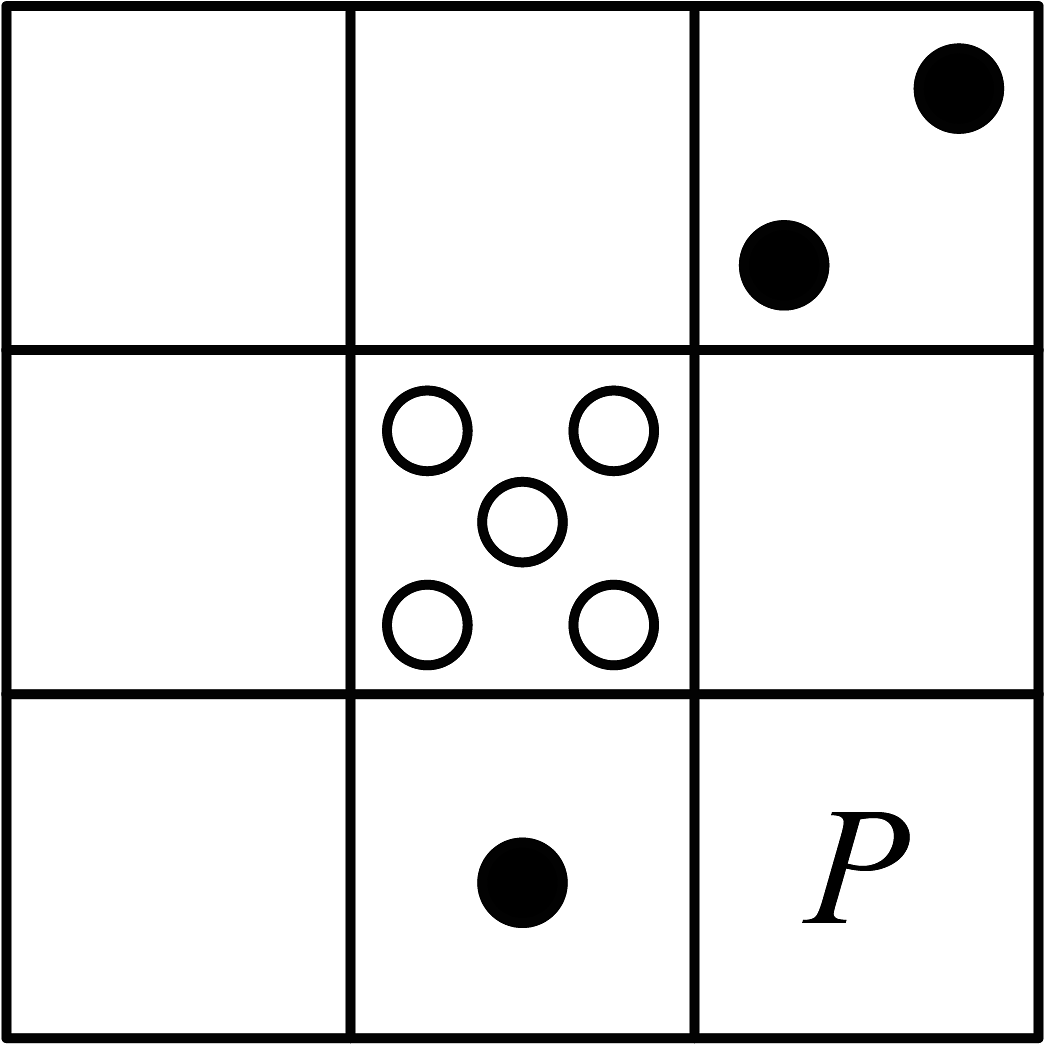 A、
A、 B、
B、 C、
C、 D、
D、 7. 长方形 和正方形 3按如图方式摆放成一个长为3322、宽为2020的长方形,则 S2的边长为( ).
7. 长方形 和正方形 3按如图方式摆放成一个长为3322、宽为2020的长方形,则 S2的边长为( ). A、651 B、655 C、656 D、662 E、6668. 现有m辆客车、n个人.若每辆客车乘40人,则还有10人不能上车:若每辆客车乘43人,则只有1人不能上车据此列出下列四个等式:①;②;③;④ . 其中正确的是( )A、①② B、②④ C、②③ D、③④
A、651 B、655 C、656 D、662 E、6668. 现有m辆客车、n个人.若每辆客车乘40人,则还有10人不能上车:若每辆客车乘43人,则只有1人不能上车据此列出下列四个等式:①;②;③;④ . 其中正确的是( )A、①② B、②④ C、②③ D、③④二、填空题:本大题共10小题,每小题3分,共30分.只要求填出最后结果.
-
9. 已知x=-3 是一元一次方程 3-ax=x的解,则a=.10. 代数式kx+4b(k≠0,且k、b为常数)的值随x取值的变化而变化,下表是当x取不同值时代数式kx+4b对应的值,则关于x的方程的解为.
x
-8
-4
0
4
8
kx+4b
4
6
8
10
12
11. 已知关于x的方程9x-3=kx+14有整数解,那么满足条件的所有整数k=.12. 我们规定两种新运算“*”和“”,其规则为a*b= ab+a-b, , 则关于x的方程5(3*x)=3的解是.13. 蛋白质和碳水化合物是我们日常饮食中的两个重要组成部分,它们都是身体所需的营养素,能够为我们提供能量,一瓶牛奶的营养成分中,碳水化合物含量是蛋白质的倍,碳水化合物,蛋白质与脂肪的含量共 . 设蛋白质的含量为 , 脂肪的含量为 , 可列出方程为 .14. 如果m , n为常数,关于x的方程 , 无论k为何值,方程的解总是 , 则 .15. 小华在计算时(☆代表一个有理数),误将“”看成“”,按照正确的运算顺序计算,结果为 , 则的正确结果是 .16. 对于两个不相等的有理数a,b,我们规定符号 min{a,b}表示a,b两数中较小的数,例如min{2,-3}=-3。按照这个规定,方程min{x,-x}=-3x-12的解为。17. 如图的号码是由12位数字组成的,每一位数字写在下面的方格中,若任何相邻的三个数字之和都等于12,则x的值为.9
x
﹣2
18. 一块长方形的瓷砖标准尺寸为 , 出于美观和保护瓷砖等原因,需要在瓷砖周边以及瓷砖之间的缝隙(缝隙宽度忽略不计)中填入美缝剂,例如图1是由两块瓷砖铺设而成,需要在、、、、处共填入的美缝剂.如果地面按图2所示的方式铺设瓷砖,当铺设5块瓷砖时,需填入的美缝剂.现在按照相同的方式给一条宽为的走廊地面铺设瓷砖后,共填入了的美缝剂,则该走廊的面积是 .
三、解答题:本大题10小题,共96分.
-
19. 解方程:(1)、;(2)、 .20. 用好错题本可以有效地积累解题方法、技巧,把握解题策略,减少再错误的可能.下面是嘉淇错题本上的一道题,请仔细阅读并完成相应的任务.
解方程: .
解:去分母,得 , …第一步
去括号,得 , …第二步
移项,得 , …第三步
合并同类项,得 , …第四步
系数化为1,得 . …第五步
任务一:
(1)填空:①以上解题过程中,第一步是依据______进行变形的;第二步去括号时用到的运算律是______.
②第______步开始出错,这一步错误的原因是______.
(2)纠正上述错误,请写出该方程的正确解答过程.
任务二:
(3)请你根据平时的学习经验,就解一元一次方程还需要注意的事项提一条建议.
21. 讨论关于x的方程|x-2|+|x-5|=a 的解的情况.(1)、当a>3时,原方程有两解.(2)、当a=3时,原方程有无数解(2≤x≤5).(3)、当a<3时,原方程无解.22. 用“”和“”定义一种新运算:对于任意有理数 , 规定: , 如: .(1)、计算:____________.(2)、若 , 则____________.(3)、若 , , , , , 当时,求的值(用含的式子表示).23. 有一个数学游戏,如图,一个数从 , , 三个位置中任选一个位置出发,按照通道内标注的要求进行运算到下一个位置.例如:将3按照(或)的顺序进行运算,即3经过“乘以”的运算得出结果. (1)、将按照的顺序进行运算,列出算式并求出运算结果.(2)、将一个数按照的顺序进行运算,发现运算结果为1.求这个数.24. 阅读与理解:
(1)、将按照的顺序进行运算,列出算式并求出运算结果.(2)、将一个数按照的顺序进行运算,发现运算结果为1.求这个数.24. 阅读与理解:定义:如果两个一元一次方程的解之和为1,我们就称这两个方程互为“美好方程”。例如:方程2x-1=3的解为x=2,方程x+1=0的解为x=-1,两个方程的解之和为1,所以这两个方程互为“美好方程”。
(1)、请判断方程4x-(x+5)=1与方程-2y-y=3是否互为“美好方程”,并说明理由。(2)、若关于x的方程与方程3x=x+4互为“美好方程”,求m的值。25. 【阅读理解】甲、乙两人分别从 A,B两地同时出发,甲骑自行车,乙骑摩托车,两人沿同一条路线相向匀速行驶,出发后经过0.4h 相遇.已知在相遇时乙比甲多行驶了14.4k m,相遇后经0.1 h乙到达A地.问:甲、乙两人的速度分别是多少?【问题分析】可以画如图所示的示意图来分析本题中的数量关系.

从图中可得到如下的相等关系:
甲行驶0.4 h的路程=乙行驶0.1 h的路程.
甲行驶0.4h的路程+14.4km=乙行驶0.4h的路程.
根据这两个相等关系,可得到甲、乙速度的关系,设元列出方程即可.
(1)、【问题解决】请你列方程解答“阅读理解”中的问题.(2)、【能力提升】对于上题,若乙出发0.2 h后行驶速度减少10 km/h,则甲出发后经过多少小时两人相距2km?26.活动目标:计算水费与用水量 素材1 为增强公民节水意识,合理利用水资源,采用“阶梯计价”. 素材2 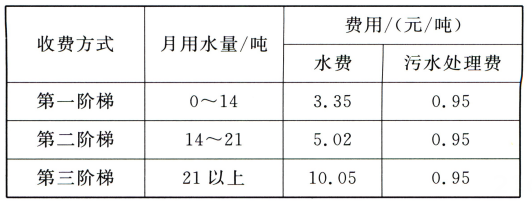
素材3 某用户 2023年2月份用水15 吨,则各种费用如下: 
问题解决 ⑴任务1 确定污水处理费 已知某用户2023年12月份所缴水费中,自来水费为66.98元,求该用户12月份需缴污水处理费多少元? ⑵任务2 确定水费 某用户 2023年11月用水a 吨,则应缴水费多少元? ⑶任务3 确定用水量 如果该用户2023年5,6月份共用水42吨(6月份用水量超过5月份用水量),共缴水费209.01元,则该用户5,6月份各用水多少吨? 27. 综合实践【素材】某商家促销电动车的方案为:A档电动车8折优惠,B档一次性降价600元.年底在原促销基础上再增加以下优惠:
新车原价
A档:2000元~3000元(含2000元,不含3000元)
B档:3000元及以上
减免
200元
300元
【问题】
(1)、若设原价为元,请用含的代数式填写实付价.新车原价
A档:2000元~3000元(含2000元,不含3000元)
B档:3000元及以上
实付价
___________元
___________元
(2)、用2120元能购买到原价为多少元的电动车?(3)、甲买了A档电动车,乙买了B档电动车,以下是他们的对话.
求甲、乙的实付价分别是多少元?
28. 将自然界的事物或现象进行“抽象”与“理想化”是科学研究的重要手段.【阅读材料】
“碰撞”在生活中无处不在,其中“弹性碰撞”是一种没有任何能量损失的碰撞,属于碰撞中的一种“理想情况”.科学家们经过研究发现,两个完全一样的物体相向运动时,如果发生弹性碰撞,会立即反向运动,且速度大小互换.例如:甲木块以的速度自西向东运动,乙木块以的速度自东向西运动,二者发生弹性碰撞后,甲木块立即变为以的速度自东向西运动,乙木块立即变为的速度自西向东运动.如果完全一样且同向运动的物体发生弹性碰撞,则运动方向不变,仅速度大小互换.
【情境呈现】
如图1,在一个长的轨道上,两个小铁球分别以、的初始速度从轨道两端沿直线相向运动,发生碰撞后,两个小铁球均反向运动,最终分别从左右两端离开轨道.如图2,若在轨道右侧添加一挡板后,小球与挡板碰撞后会反弹,最后两个小球都会从左侧离开轨道.

【情境转化】
为便于研究,我们可以将上述过程进行“抽象”与“理想化”:两小球完全一样且体积忽略不计,可以看作两个点,小球运动速度只会因为碰撞而发生改变,小球与小球的碰撞为“弹性碰撞”,小球与挡板碰撞后立即以原速度反向运动.由此,我们可以使用数轴来表示轨道,数轴上点的运动来表示小球的运动.如图3建立数轴,点从原点点出发,沿正方向以4个单位长度的速度匀速运动,点从点出发,沿负方向以1个单位长度的速度匀速运动.若点运动到线段之外,则认为小球离开轨道.已知 .

【问题解决】
若两小球(、两点)同时出发,、两点在轨道上的运动时间分别为、秒,请回答以下问题:
(1)、如图3,两小球第一次相遇时,_____.根据计算,我们可以得知点代表的小球会先从右侧离开轨道,则它离开轨道的瞬间,_____.(2)、如图4,在点所在位置放置挡板,则点代表的小球在到达点后会立即反向运动,速度不变.请求出两小球第二次相遇时的值.(3)、在(2)的条件下,将轨道沿射线的方向进行延长,设延长至点,如图5,则需要延长多少个单位长度(即的长度为何值时),才能使得?