第十五章《轴对称图形和等腰三角形》基础卷—沪科版数学八（上）单元分层测

试卷更新日期：2025-09-21 类型：单元试卷

进入出卷网下载

一、选择题：本大题共12小题，每小题3分，在每小题给出的四个选项中，只有一个是正确的.每小题选对得3分，选错、不选或多选，均不得分.

1. 第33届夏季奥运会于2024年7月26日至8月11日在法国巴黎举行，中国取得金牌榜第一名的好成绩，如图所示巴黎奥运会项目图标中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. “观成爱我”的首字母缩写为G、C、A、W，其中不是轴对称图形的选项是（　　）

A、 B、 C、 D、

查看试题解析
3. 如图所示，△ABC与△DEF 关于直线l对称，下列说法错误的是（）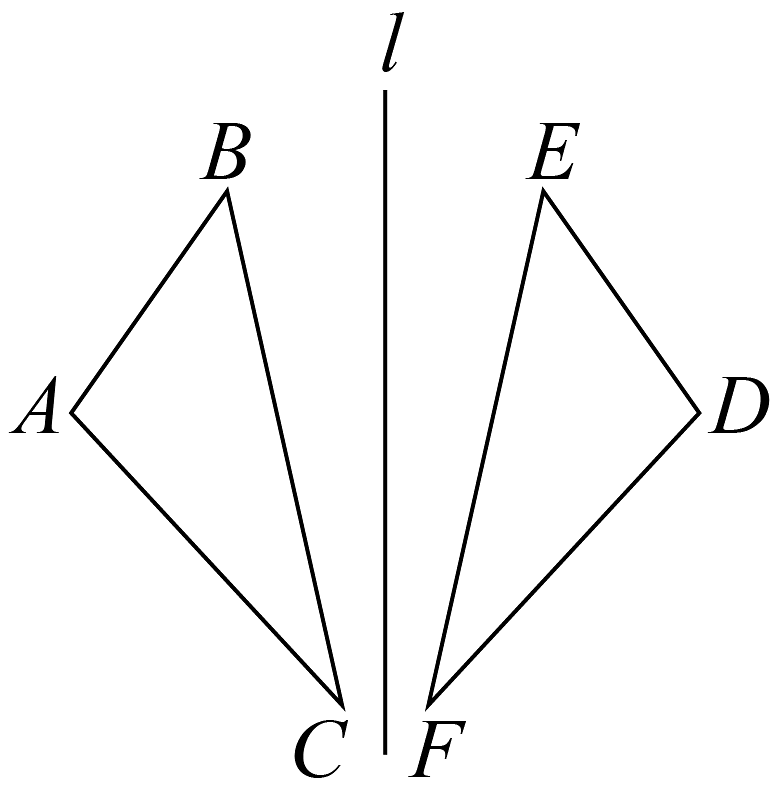

A、AB=DE B、∠BAC=∠EDF C、点B和点E到直线l的距离相等 D、AC $∥$ DE

查看试题解析
4. 在联欢晚会上，有 $A$ 、 $B$ 、 $C$ 三名同学站在一个三角形的三个顶点位置上，他们在玩抢凳子游戏，要求在他们中间放一个木凳，谁先抢到凳子谁获胜，为使游戏公平，则凳子应放的最适当的位置在 $△ A B C$ 的（）

A、三边中线的交点 B、三条角平分线的交点 C、三边上高的交点 D、三条垂直平分线的交点

查看试题解析
5. 通过下列尺规作图，能确定BD=CD的是（）

A、 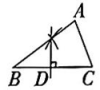B、 C、 D、

查看试题解析
6. 如图，在 $△ A B C$ 中， $A B = A C = 8 ， B C = 5$ ，线段 $A B$ 的垂直平分线交 $A B$ 于点E，交 $A C$ 于点D，则 $△ B D C$ 的周长为（）

A、21 B、14 C、13 D、9

查看试题解析
7. 如图，∠B=∠C=90°，M是BC 的中点，DM平分∠ADC，且∠ADC=110°，则∠MAB 的度数为( ).

A、30° B、35° C、45° D、60°

查看试题解析
8. 观察下列作图痕迹，所作线段 $C D$ 为 $△ A B C$ 的角平分线的是（）

A、 B、 C、 D、

查看试题解析
9. 在 $Rt △ ABC$ 中， $∠ C = 90 °$ ， $∠ BAC$ 的角平分线 $AD$ 交 $BC$ 于点 $D ， BC = 7 ， BD = 4$ ，则点 $D$ 到 $AB$ 的距离是（）

A、2 B、3 C、4 D、5

查看试题解析
10. 如图是跷跷板示意图，横板AB绕中点O 上下转动，立柱 OC与地面垂直，当横板AB 的A 端着地时，测得∠OAC=30°，若OC=0.5m ，则AB 的长为 ( )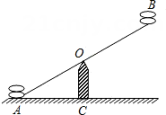

A、0.5m B、1m C、1.5m D、2m

查看试题解析
11. 如图，在△ABC中，AB=AC，AD、CE是△ABC的两条中线，P是AD上一个动点，则下列线段的长度等于BP+EP最小值的是（）

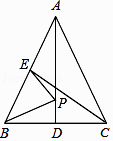A、BC B、CE C、AD D、AC

查看试题解析
12. 如图，A、C、B三点在同一条直线上， $△ D A C$ 和 $△ E B C$ 都是等边三角形， $A E 、 B D$ 分别与 $C D 、 C E$ 交于点M、N，有如下结论：① $A E = B D$ ；② $C M = C N$ ；③ $A M = D N$ ；④ $△ C M N$ 是等边三角形；其中，正确结论的个数是（）

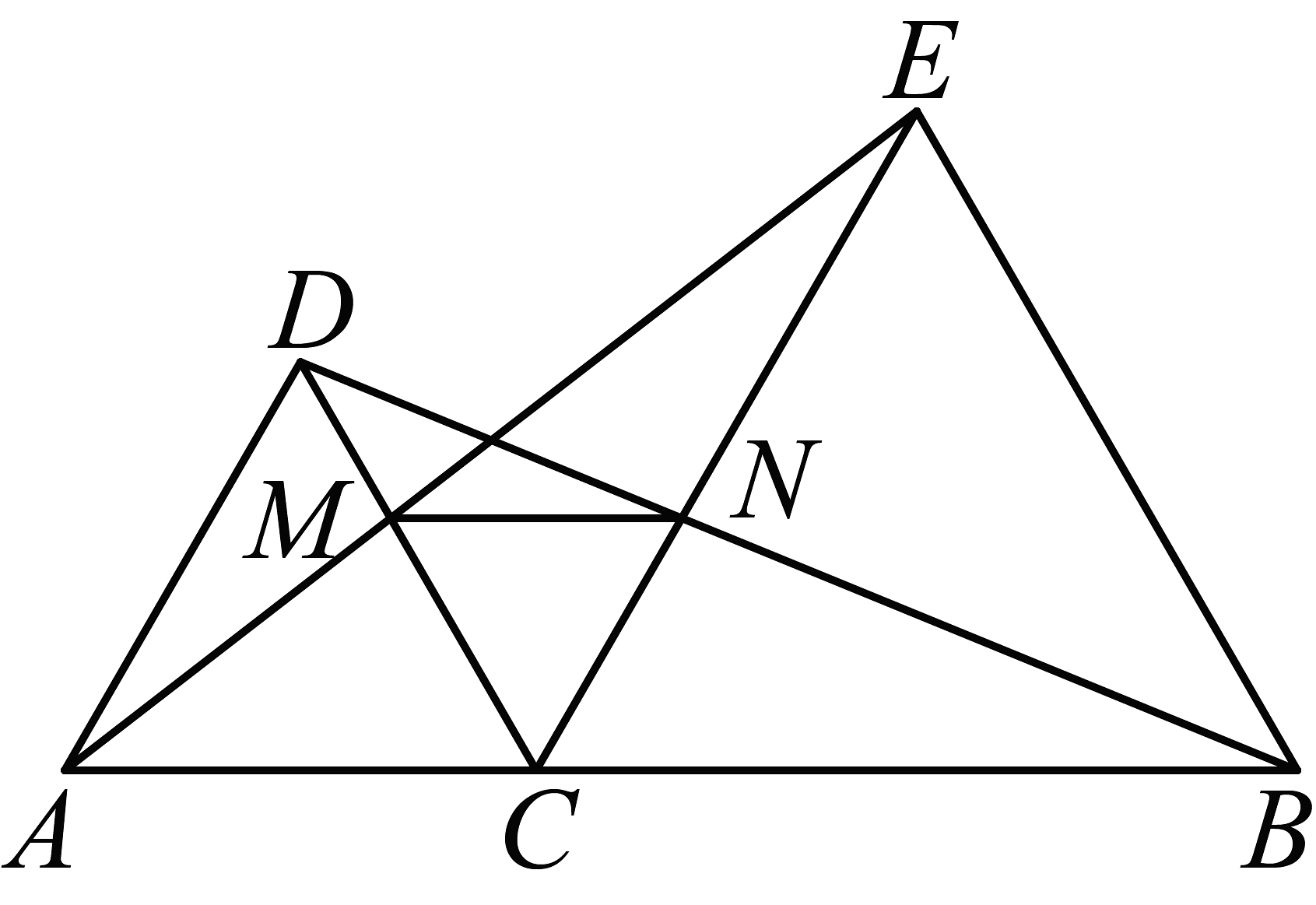A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题：本大题共4小题，每小题4分，共16分.只要求填出最后结果.

13. 如图， $A B$ 左边是计算器上的数字“5”，若以直线 $A B$ 为对称轴，则它的轴对称图形是数字.

查看试题解析
14. 如图，一个加油站恰好位于两条公路 $m$ ， $n$ 所夹角的平分线上，若加油站到公路 $m$ 的距离是 $80 m$ ，则它到公路 $n$ 的距离是 $m$ ．

查看试题解析
15. 如图，在△ABC中，EF是AB的垂直平分线，与AB交于点D，BF=6，CF=2，则AC=.

查看试题解析
16. “等边三角形中有一个内角等于60°”的的逆命题是，这个逆命题(填“成立”或“不成立”).

查看试题解析

三、解答题：本大题共8小题，共68分.

17. 在 $4 \times 4$ 的正方形网格中建立如图1、2所示的直角坐标系，其中格点A，B的坐标分别是 $(0, 1), (- 1, - 1)$ ．

(1)、请图1中添加一个格点 $C$ ，使得 $△ A B C$ 是轴对称图形，且对称轴经过点 $(0, 1)$ ．

(2)、请图2中添加一个格点 $D$ ，使得 $△ A B D$ 也是轴对称图形，且对称轴经过点 $(1, 1)$ ．

查看试题解析
18. 如图，在 Rt $△ A B C$ 中， $∠ C = 90^{\circ}$ 。

(1)、尺规作图：作 AB 的垂直平分线 $D E$ ，交 BC 于点 D ，交 AB 于点 E （不写作法，保留作图痕迹）；

(2)、在（1）题图中，连接 AD ，若 $A D$ 平分 $∠ C A B$ ，且 $∠ B = 30^{\circ}, D E = 3$ ，求 $B C$ 的长。

查看试题解析
19. 如图，在△ABC中，∠C=90°，AD平分∠BAC，AB=17，DC=5，求S_△_ABD.

查看试题解析
20. 如图， AD 是△ABC的角平分线， DE⊥AB，DF⊥AC，垂足分别为E， F，连接EF，EF 与AD 相交于点G. AD 与EF 垂直吗?证明你的结论.

查看试题解析
21. 如图，点 $C$ 在线段 $A B$ 上， $A D / / E B$ ， $A C = B E$ ， $A D = B C$ ， $C F$ 平分 $∠ D C E$ ．

(1)、证明： $△ A D C$ ≌ $△ B C E$ ；

(2)、若 $C F = 3$ ， $D F = 4$ ，求 $△ D C E$ 的面积．

查看试题解析
22.

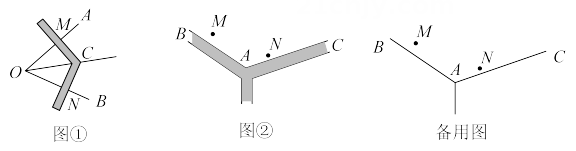(1)、【问题情境】
我国古代已经用角尺平分任意角，做法如下：如图①，在 $∠ A O B$ 的边 $O A$ ， $O B$ 上分别取 $O M = O N$ ，移动角尺，使角尺两边相同刻度分别与点 $M, N$ 重合，则过角尺顶点 $C$ 的射线 $O C$ 是 $∠ A O B$ 的平分线．请说明此做法的理由；

(2)、【拓展实践】
某公园的两条小路 $A B$ 和 $A C$ ，汇聚形成了一个岔路口 $A$ （如图②），现要在两条小路之间安装一盏路灯 $E$ ，使得路灯照亮两条小路（两条小路一样亮），并且路灯 $E$ 到休息椅 $M$ 和 $N$ 的距离相等．问路灯应该安装在哪个位置？请用不带刻度的直尺和圆规在对应的备用图中作出路灯 $E$ 的位置．（保留作图痕迹，不写作法）

查看试题解析
23. 如图，在△ABC 中，已知∠ACB=90°，AC=BC，D 是边AB 上的动点，连接CD，点 B 关于直线CD 的对称点为E，射线AE 与射线CD 交于点 F.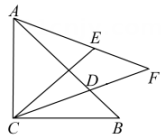

(1)、连接CE，求证：∠CAE=∠CEA.

(2)、当 BD<AD时，求∠AFC 的度数.

(3)、若AD=AC，求证：AE=CD.

查看试题解析
24. 如图，在 $△ A B C$ 中， $∠ C = 9 0^{°}, 6 0^{°} < ∠ A B C < 9 0^{°}$ .点 $E$ 在边AB上，点 $D$ 在CB延长线，且满足 $B D = B E$ .连接 $D E, A D$ .已知 $∠ C A D = ∠ B E D$ .

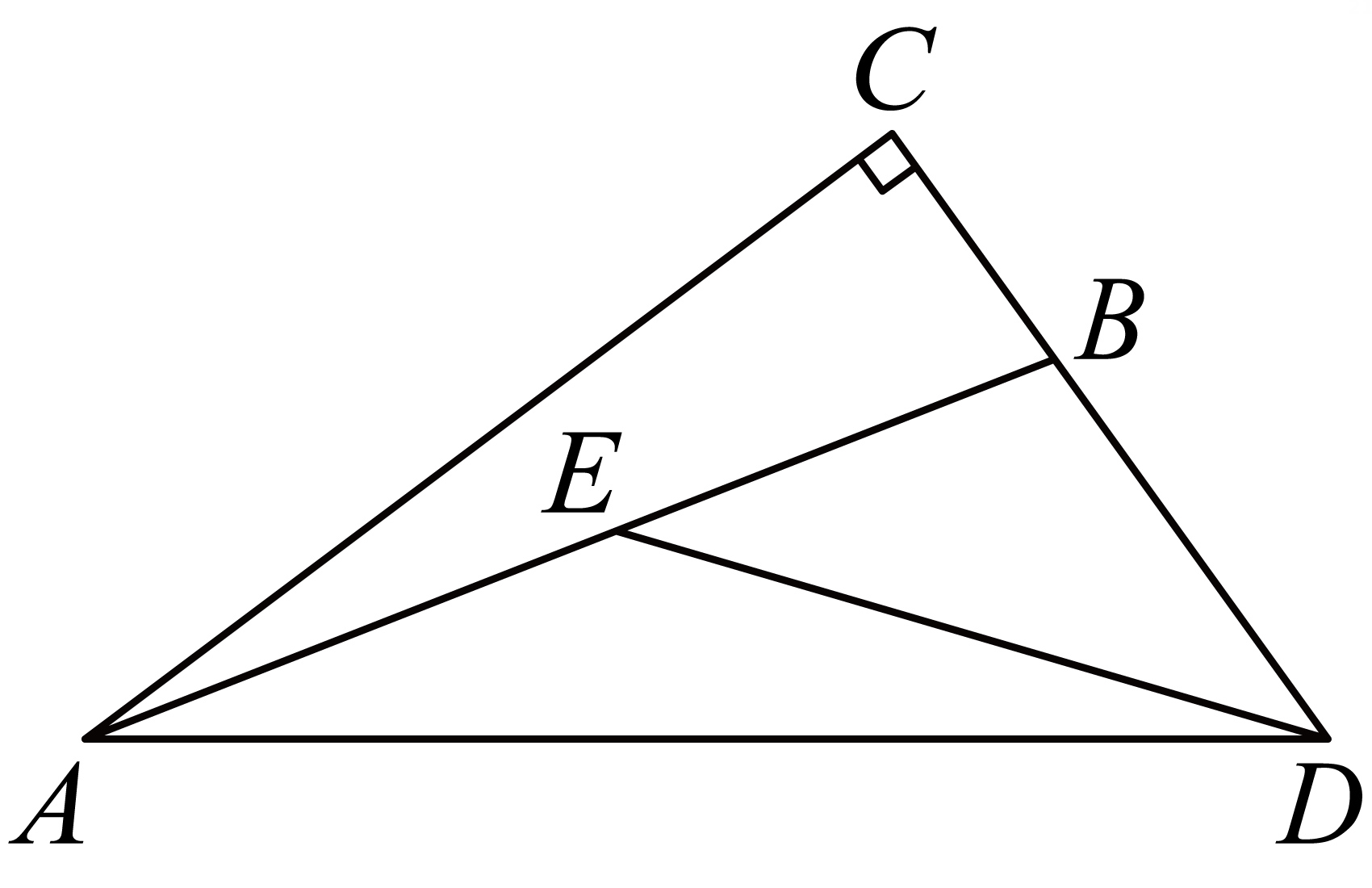(1)、若 $∠ B E D = 4 0^{°}$ ，求 $∠ B A D$ 的度数.

(2)、小真同学通过画图和测量得到以下近似数据：
AE
4cm
6cm
8cm
10cm
BC
2cm
3cm
4cm
5cm
猜想：AE与BC之间的等量关系，并给出证明.

(3)、探究 $A D, A B, B D$ 三者之间的等量关系，并给出证明.

查看试题解析

AE	4cm	6cm	8cm	10cm
BC	2cm	3cm	4cm	5cm