第十五章《轴对称图形和等腰三角形》提升卷—沪科版数学八(上)单元分层测
试卷更新日期:2025-09-21 类型:单元试卷
一、选择题:本大题共12小题,每小题3分,在每小题给出的四个选项中,只有一个是正确的.每小题选对得3分,选错、不选或多选,均不得分.
-
1. 如图,弹性小球从点出发,沿所示方向运动,每当小球碰到矩形的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为 , 第2次碰到矩形的边时的点为 , ……;第2024次碰到矩形的边时的点为图中的( )
 A、点 B、点 C、点 D、点2. 如图,在平面直角坐标系中,对进行循环往复的轴对称变换,若原来点A坐标是 , 则经过第2021次变换后点A的对应点的坐标为( )
A、点 B、点 C、点 D、点2. 如图,在平面直角坐标系中,对进行循环往复的轴对称变换,若原来点A坐标是 , 则经过第2021次变换后点A的对应点的坐标为( ) A、 B、 C、 D、3. 风筝又称“纸鸢”“风鸢”等,起源于东周春秋时期,距今已有2 000多年的历史.如图是一款风筝骨架的简化图,已知 , , , , 制作这个风筝需要的布料至少为( )
A、 B、 C、 D、3. 风筝又称“纸鸢”“风鸢”等,起源于东周春秋时期,距今已有2 000多年的历史.如图是一款风筝骨架的简化图,已知 , , , , 制作这个风筝需要的布料至少为( ) A、 B、 C、 D、4. 如图,在中, , , 分别以点和点为圆心,大于的长为半径画弧,两弧相交的两侧于点、 , 连接 , 交于点 , 连接 , 则的度数为( )
A、 B、 C、 D、4. 如图,在中, , , 分别以点和点为圆心,大于的长为半径画弧,两弧相交的两侧于点、 , 连接 , 交于点 , 连接 , 则的度数为( ) A、 B、 C、 D、5. 在学习了角平分线的相关知识后,小华和小丽分别设计了一种作一个角的平分线的方法:
A、 B、 C、 D、5. 在学习了角平分线的相关知识后,小华和小丽分别设计了一种作一个角的平分线的方法:小华
小丽
在∠AOB 中,将两把完全相同的直尺按照如图①所示的方式摆放,则射线 OP为∠AOB 的平分线.

图①
将两个完全相同的等腰直角三角尺按如图②所示摆放,使两个三角尺的斜边分别和∠ABC的两边重叠,两个三角尺的直角顶点重合为顶点P,作射线 BP,则 BP 为∠ABC的角平分线.
 图②
图②则两位同学的作法( )
A、小华正确,小丽错误 B、小华错误,小丽正确 C、两人均正确 D、两人均错误6. 下面是作业本上的一道习题,小可,小雨,小齐,小梦四位同学的作法中,错误的是( )题目:
如图,在△ABC 中,∠B=80°,∠C=40°,借助尺规,在直线AC 上找一点 D,连接 BD,使得∠CBD=∠C.
 A、
A、 小可的作法
B、
小可的作法
B、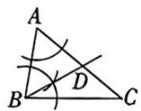 小雨的作法
C、
小雨的作法
C、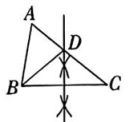 小齐的作法
D、
小齐的作法
D、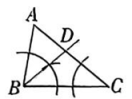 小梦的作法
7. 如图,已知每个小方格的边长为1,A,B两点都在小方格的顶点上,请在图中找一个顶点C,使△ABC为等腰三角形,则这样的顶点C有( )
小梦的作法
7. 如图,已知每个小方格的边长为1,A,B两点都在小方格的顶点上,请在图中找一个顶点C,使△ABC为等腰三角形,则这样的顶点C有( ) A、8个 B、7个 C、6个 D、5个8. 如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,则下列四个结论:①AD上任意一点到点C、点B的距离相等;②AD上任意一点到AB,AC的距离相等;③BD=CD,AD⊥BC;④∠BDE=∠CDF.其中,正确的个数是( )
A、8个 B、7个 C、6个 D、5个8. 如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,则下列四个结论:①AD上任意一点到点C、点B的距离相等;②AD上任意一点到AB,AC的距离相等;③BD=CD,AD⊥BC;④∠BDE=∠CDF.其中,正确的个数是( ) A、1 B、2 C、3 D、49. “一亭幽绝费平章,峡口清风赠晚凉.前度桃花斗红紫,今来枫叶染丹黄.饶将春色输秋色,迎过朝阳送夕阳.此地四时可乘兴,待谁招鹤共翱翔.”其中“一亭”指的是具有一座悠久历史的古典园林建筑——“爱晚亭”.如图,“爱晚亭”的顶端可看作等腰三角形 , , D是边上的一点.下列条件不能说明是的角平分线的是( )
A、1 B、2 C、3 D、49. “一亭幽绝费平章,峡口清风赠晚凉.前度桃花斗红紫,今来枫叶染丹黄.饶将春色输秋色,迎过朝阳送夕阳.此地四时可乘兴,待谁招鹤共翱翔.”其中“一亭”指的是具有一座悠久历史的古典园林建筑——“爱晚亭”.如图,“爱晚亭”的顶端可看作等腰三角形 , , D是边上的一点.下列条件不能说明是的角平分线的是( )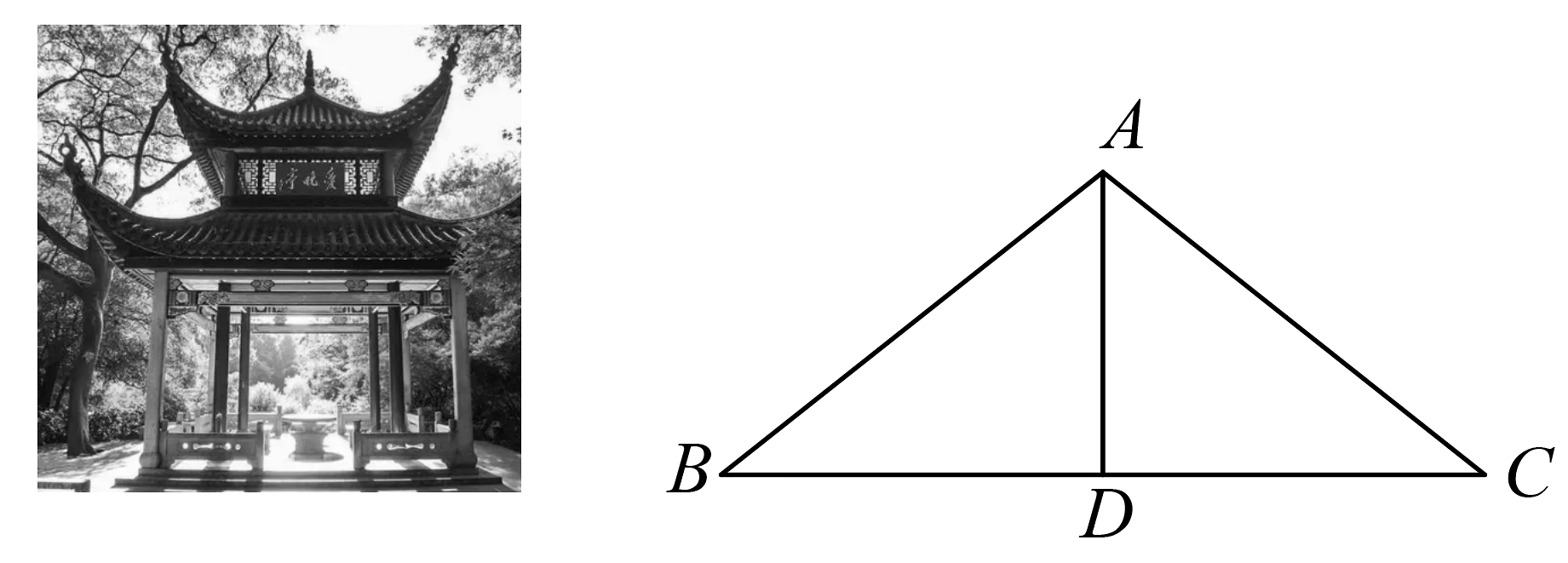 A、 B、 C、 D、与的周长相等10. 如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A'处,折痕为DE . 如果∠A=α,∠DEA=β,∠CEA'=γ,∠BDA'=θ,那么下列式子中不一定成立的是( )
A、 B、 C、 D、与的周长相等10. 如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A'处,折痕为DE . 如果∠A=α,∠DEA=β,∠CEA'=γ,∠BDA'=θ,那么下列式子中不一定成立的是( ) A、θ=2α+γ B、θ=180°﹣α﹣γ C、β= D、θ=2α+2β﹣180°11. 已知,如图,是等边三角形, , 于 , 交于点 , 下列说法:① , ② , ③ , ④ , 其正确的结论有( ).
A、θ=2α+γ B、θ=180°﹣α﹣γ C、β= D、θ=2α+2β﹣180°11. 已知,如图,是等边三角形, , 于 , 交于点 , 下列说法:① , ② , ③ , ④ , 其正确的结论有( ). A、①②④ B、①②③ C、②③④ D、①③④12. 如图,等腰Rt△ABC 中,∠BAC=90°,AD=AE,BE 和CD 交于点N,AF⊥BE,FG⊥CD 交 BE 的延长线于点 G.下列说法:①∠ABE=∠FAC;②AN 垂直平分BC;③GE=GM;④BG=AF+FG,其中正确的个数是( ).
A、①②④ B、①②③ C、②③④ D、①③④12. 如图,等腰Rt△ABC 中,∠BAC=90°,AD=AE,BE 和CD 交于点N,AF⊥BE,FG⊥CD 交 BE 的延长线于点 G.下列说法:①∠ABE=∠FAC;②AN 垂直平分BC;③GE=GM;④BG=AF+FG,其中正确的个数是( ).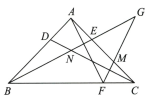 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题:本大题共4小题,每小题4分,共16分.只要求填出最后结果.
-
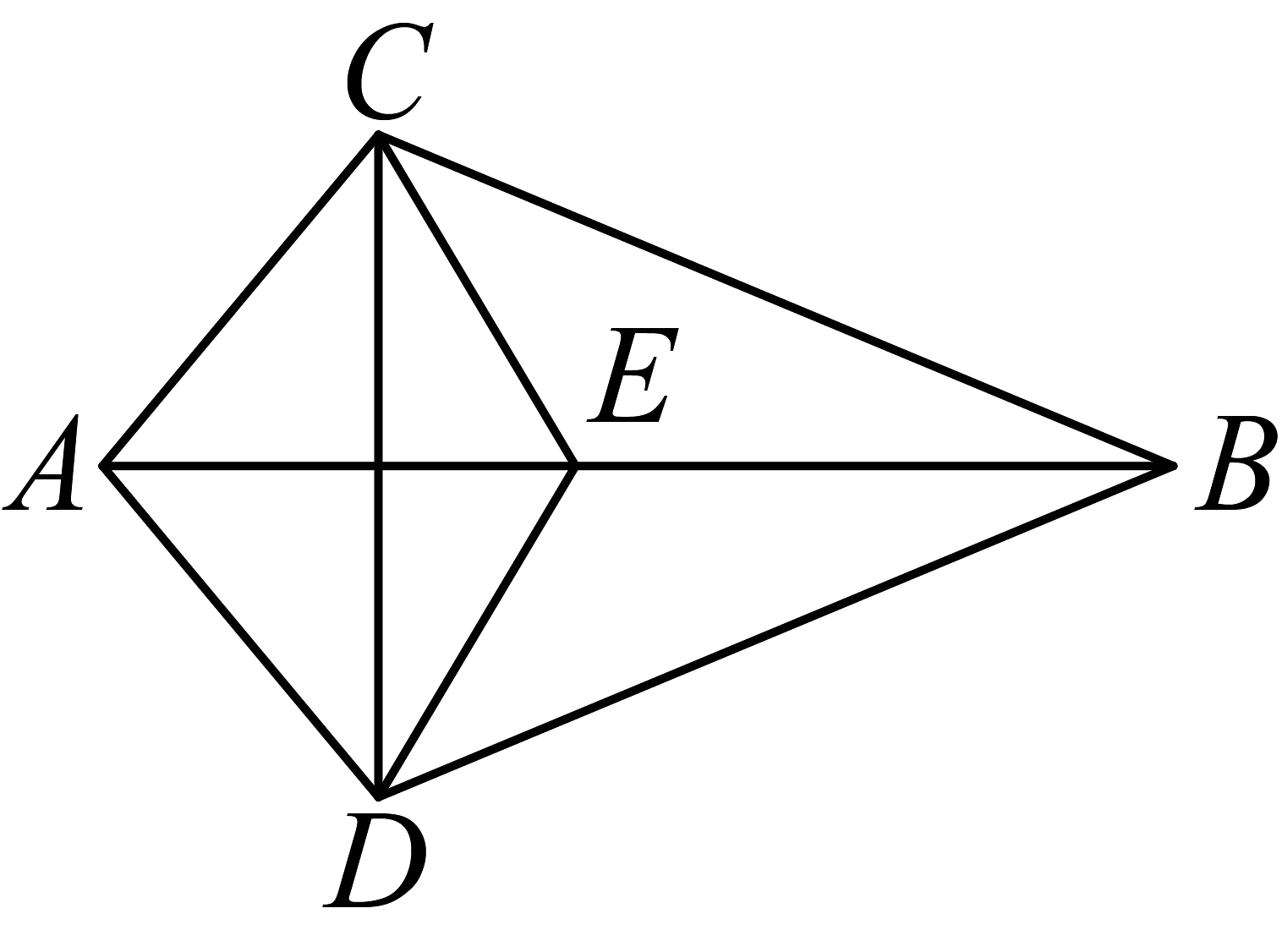
13. 镜中像 站在一个平面镜面前,大家总能看到自己的像.如果你站在两个有夹角的平面镜前,通常镜子中能看到不止两个你的像.那么当两个平面镜的夹角为60°时,共可以呈现个你的像.14. 如图,已知平分 , , 在上,结论:①;②;③平分;④所在的直线是的垂直平分线.其中正确的是(填序号)
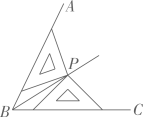
 15. 如图所示,和的角平分线相交于点P, , 则的度数为 .
15. 如图所示,和的角平分线相交于点P, , 则的度数为 . 16. 如图,中, , , 若点是直线上一动点,连接 , 以为边作等边三角形 , 若 , 求的最小距离为 .
16. 如图,中, , , 若点是直线上一动点,连接 , 以为边作等边三角形 , 若 , 求的最小距离为 .
三、解答题:本大题共8小题,共68分.
-
17. 如图,在平面直角坐标系中;的三个顶点坐标分别为 , , .
 (1)、请画出将向右平移7个单位得到的;(2)、请画出与关于轴对称的 , 并写出的坐标;(3)、在轴上找一点使得的面积为3,直接写出点的坐标.18. 第五代移动通信技术(简称5G)是最新一代蜂窝移动通信技术,是4G、3G和2G系统后的延伸.5G的性能目标是高数据速率、减少延迟、节省能源、降低成本、提高系统容量和大规模设备连接.县电信部门要修建一座5G信号发射塔,要求发射塔离村庄A、B的距离必须相等,且到两条高速公路MN、PQ的距离也必须相等.发射塔点G应修建在什么位置?在图上标出它的位置.(请保留作图痕迹,并标注出点G,否则扣分.)
(1)、请画出将向右平移7个单位得到的;(2)、请画出与关于轴对称的 , 并写出的坐标;(3)、在轴上找一点使得的面积为3,直接写出点的坐标.18. 第五代移动通信技术(简称5G)是最新一代蜂窝移动通信技术,是4G、3G和2G系统后的延伸.5G的性能目标是高数据速率、减少延迟、节省能源、降低成本、提高系统容量和大规模设备连接.县电信部门要修建一座5G信号发射塔,要求发射塔离村庄A、B的距离必须相等,且到两条高速公路MN、PQ的距离也必须相等.发射塔点G应修建在什么位置?在图上标出它的位置.(请保留作图痕迹,并标注出点G,否则扣分.) 19. 如图,小球起始时位于 (3,0)处,沿所示的方向击球,小球运动的轨迹如图所示,用坐标描述这个运动,找出小球运动的轨迹上几个关于直线 l 对称的点.如果小球起始时位于(1,0)处,仍按原来方向击球,请你画出这时小球运动的轨迹.
19. 如图,小球起始时位于 (3,0)处,沿所示的方向击球,小球运动的轨迹如图所示,用坐标描述这个运动,找出小球运动的轨迹上几个关于直线 l 对称的点.如果小球起始时位于(1,0)处,仍按原来方向击球,请你画出这时小球运动的轨迹. 20. 如图,已知点在的内部,且点与点关于对称,交于点 , 点与点关于对称,交于点分别交于点 .
20. 如图,已知点在的内部,且点与点关于对称,交于点 , 点与点关于对称,交于点分别交于点 . (1)、连接 , 若 , 求的周长;(2)、若 , 求证:平分 .21. 如图1是一种升降阅读架,由面板、支撑轴和底座构成,图2是其侧面结构示意图,面板固定在支撑轴端点处, , 支撑轴长 , 支撑轴与底座所成的角 .
(1)、连接 , 若 , 求的周长;(2)、若 , 求证:平分 .21. 如图1是一种升降阅读架,由面板、支撑轴和底座构成,图2是其侧面结构示意图,面板固定在支撑轴端点处, , 支撑轴长 , 支撑轴与底座所成的角 .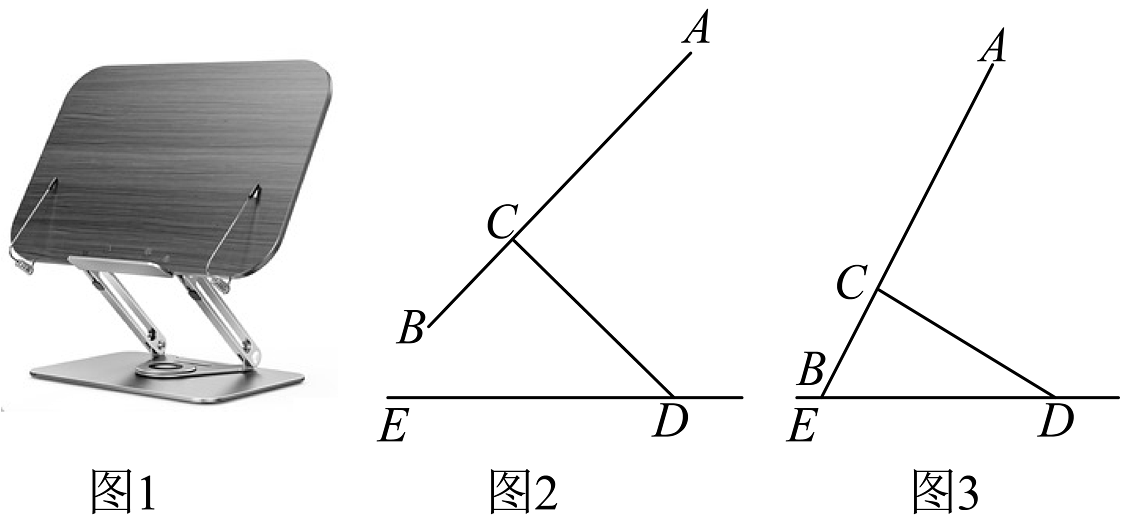 (1)、求端点到底座的距离;(2)、如图3,为了阅读舒适,将绕点逆时针旋转后,点恰好落在直线上,问:端点到底座的距离减少了多少?22. 如图,△ABC中,AD⊥BC,点E在AC的垂直平分线上,且 BD=DE.
(1)、求端点到底座的距离;(2)、如图3,为了阅读舒适,将绕点逆时针旋转后,点恰好落在直线上,问:端点到底座的距离减少了多少?22. 如图,△ABC中,AD⊥BC,点E在AC的垂直平分线上,且 BD=DE. (1)、如果∠BAE= 40°,那么∠B=° ,∠C=° ;(2)、如果△ABC的周长为13cm,AC=6cm,那么△ABE的周长=cm;(3)、你发现线段AB与BD的和等于图中哪条线段的长,并证明你的结论.23. 【概念学习】
(1)、如果∠BAE= 40°,那么∠B=° ,∠C=° ;(2)、如果△ABC的周长为13cm,AC=6cm,那么△ABE的周长=cm;(3)、你发现线段AB与BD的和等于图中哪条线段的长,并证明你的结论.23. 【概念学习】规定①:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“形似三角形”.
规定②:从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“形似三角形”,我们把这条线段叫做这个三角形的“等腰分割线”.
 (1)、【概念理解】
(1)、【概念理解】如图1,在△ABC中,∠A=36°,AB=AC,CD平分∠ACB,则△CBD与△ABC(填“是”或“不是”)互为“形似三角形”.
(2)、如图2,在△ABC中,CD平分∠ACB,∠A=36°,∠B=48°.求证:CD为△ABC的等腰分割线;(3)、【概念应用】在△ABC中,∠A=45°,CD是△ABC的等腰分割线,直接写出∠ACB的度数.
24. 【阅读材料】证明两条线段相等,常用的方法是应用全等三角形或等腰三角形的性质.如果两条线段不在同一个三角形中,且所在三角形明显不全等,此时就需要添加辅助线来构造全等三角形. (1)、【理解应用】如图(1)所示,在等腰三角形ABC中,AB=AC,D为BC上一点,且CD>BD,连接AD,小明对△ABC进行了如下操作:在CD上取一点E,使得AE=AD,连接AE,则可证明△ABD≌△ACE,请你补充小明操作过程的证明;(2)、【类比探究】如图(2)所示,在四边形ABCD中,AC平分∠BAD,∠ABC+∠ADC=180°,求证:CD=CB;(3)、【拓展应用】如图(3)所示,已知△ABC是边长为5 cm的等边三角形,点E在CA的延长线上,且AE=1.5 cm,连接EB,在线段BC上取点F,连接EF,使得EB=EF,请直接写出BF的长.
(1)、【理解应用】如图(1)所示,在等腰三角形ABC中,AB=AC,D为BC上一点,且CD>BD,连接AD,小明对△ABC进行了如下操作:在CD上取一点E,使得AE=AD,连接AE,则可证明△ABD≌△ACE,请你补充小明操作过程的证明;(2)、【类比探究】如图(2)所示,在四边形ABCD中,AC平分∠BAD,∠ABC+∠ADC=180°,求证:CD=CB;(3)、【拓展应用】如图(3)所示,已知△ABC是边长为5 cm的等边三角形,点E在CA的延长线上,且AE=1.5 cm,连接EB,在线段BC上取点F,连接EF,使得EB=EF,请直接写出BF的长.