第三章《代数式》提升卷—苏科版数学七（上）单元测

试卷更新日期：2025-09-21 类型：单元试卷

进入出卷网下载

一、选择题：本大题共8小题，每小题3分，共24分.在每小题给出的四个选项中，只有一个是正确的.每小题选对得3分，选错、不选或多选，均不得分.

1. 已知一个代数式是三次四项式，这个代数式可以是（）

A、 $x^{2} + x y - 5 y + 2$ B、 $x^{3} + 5 x + 1$ C、 $6 x y^{3} + 3 x^{3} + 7 x - 5$ D、 $3 x + x^{2} y - 3 y + 6$

查看试题解析
2. 如图所示为由两个正方形和一个半径为a 的半圆组合而成的图形.已知两个正方形的边长分别为a，b（a>b），则图中阴影部分的面积为( )

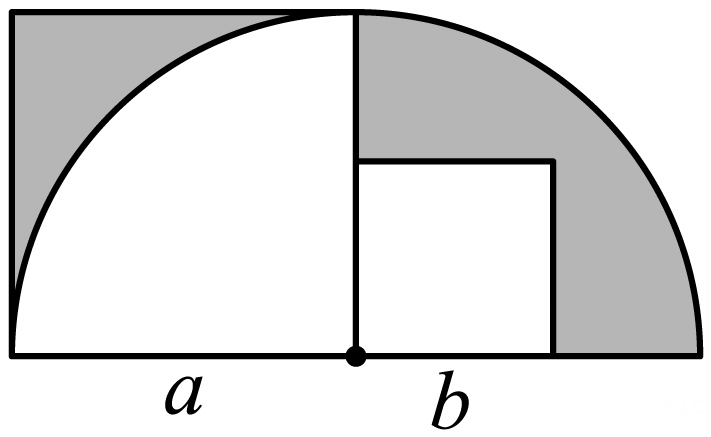A、 $a^{2} + b^{2} - \frac{π a^{2}}{2}$ B、 $a^{2} - b^{2} + \frac{π a^{2}}{2}$ C、 $a^{2} - b^{2} - \frac{π a^{2}}{2}$ D、 $a^{2} - b^{2}$

查看试题解析
3. 如图所示的运算程序中，若开始输入的x 值为48，我们发现第一次输出的结果为24，第二次输出的结果为12……则第2010 次输出的结果为( ).

A、6 B、3 C、 $\frac{3}{2^{2006}}$ D、 $\frac{3}{2^{1003}}$

查看试题解析
4. 如图，小明计划将正方形菜园 $A B C D$ 分割成三个长方形①②③和一个正方形④．若长方形②与③的周长和为 $30 m$ ，则正方形 $A B C D$ 与正方形④的周长和为（　　）

A、 $30 m$ B、 $40 m$ C、 $55 m$ D、 $60 m$

查看试题解析
5. 如图，现有五张图 1 所示形状大小完全相同的小长方形，长为 $a$ ，宽为 $b$ ，将它们放入图 2 的大长方形 $A B C D$ 中，若未被覆盖的两个阴影部分的周长分别记为 $C_{1}$ 和 $C_{2}, C_{1}$ 与 $C_{2}$ 的差等于两倍的小长方形的宽，则小长方形的长与宽满足（）

A、 $a = \frac{7}{2} b$ B、 $a = 3 b$ C、 $a = \frac{5}{2} b$ D、 $a = 2 b$

查看试题解析
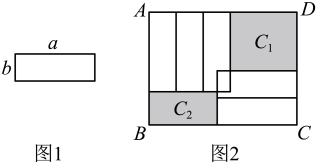6. 如图，在一个大长方形中放入三个边长不等的小正方形①，②，③，若要求两个阴影部分的周长差，只要知道下列哪两条线段的差的绝对值（）

A、|AB-CD| B、|CD-EF| C、|DE-CD| D、|DE-EF|

查看试题解析
7. 9月16号，杭州亚运村举行开村仪式暨中国体育代表团欢迎仪式，有 $n$ 位运动员乘坐 $m$ 辆车，若每辆车载 $30$ 人，则还有 $7$ 人不能上车；若每辆车载 $35$ 人，则最后一辆车空了 $6$ 个座位．①运动员有 $(30 m + 7)$ 人；②运动员有 $(35 m - 6)$ 人；③运动员乘坐的车有 $\frac{n + 7}{30}$ 辆；④运动员乘坐的车有 $\frac{n + 6}{35}$ 辆．其中正确的是（）

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析
8. 把四张形状和大小完全相同的小长方形卡片（如图1）分两种不同形式不重叠地放在一个长为m，宽为n的长方形盒子底部（如图2、图3），盒子底面未被卡片覆盖的部分用阴影表示.设图2中阴影部分图形的周长为l₁ ，图3中两个阴影部分图形的周长和为l₂ ，若 $l_{1} = \frac{5}{4} l_{2} ，$ 则m，n满足（）

A、 $m = \frac{6}{5} n$ B、 $m = \frac{7}{5} n$ C、 $m = \frac{3}{2} n$ D、 $m = \frac{9}{5} n$

查看试题解析

二、填空题：本大题共10小题，每小题3分，共30分.只要求填出最后结果.

9. 当m=时，关于x的多项式 $8 x^{2} - 3 x + 5$ 与多项式 $3 x^{2} + 4 m x^{2} - 5 x + 3$ 的和中不含 $x^{2}$ 项．

查看试题解析
10. 甲、乙、丙三人一起进行百米赛跑(假定三人均为匀速直线运动)，如果当甲到达终点时，乙距终点还有5米，丙距终点还有10 米，那么当乙到达终点时，丙距终点还有米.

查看试题解析
11. 某快递公司同城寄件的收费标准如下：寄一件物品，不超过1千克时付费10元；超出1千克的部分每千克加收2元.乐乐在该公司向同城内的另一地寄一件物品，物品重x(x>1)千克，则他需支付元(用含x的代数式表示).

查看试题解析
12. 如图，在正方形 $A B C D$ 中放入正方形 $A E F G$ 和正方形 $B H I E$ ，点 $E$ 在 $A B$ 上，且点 $F, I, E$ 在一条直线上．若阴影部分面积为 $6 x, D G = 2$ ，则阴影部分周长为．（用含 $x$ 的代数式表示）

查看试题解析
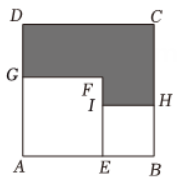13. 如图，一个瓶身为圆柱体的玻璃瓶内装有高 $a$ 厘米的墨水，将瓶盖盖好后倒置，墨水水面高为 $h$ 厘米，则瓶内的墨水的体积约占玻璃瓶容积的．

查看试题解析
14. 某数学老师在课外活动中做了一个有趣的游戏：首先发给A、B、C三个同学相同数量的扑克牌（假定发到每个同学手中的扑克牌数量足够多），然后依次完成以下三个步骤：
第一步，A同学拿出五张扑克牌给B同学；
第二步，C同学拿出三张扑克牌给B同学；
第三步，A同学手中此时有多少张扑克牌，B同学就拿出多少张扑克牌给A同学．
请你确定，最终B同学手中剩余的扑克牌的张数为．

查看试题解析
15. 定义：对于一个数x ，我们把 $[x]$ 称作x的相伴数：若 $x \geq 0$ ，则 $[x] = x - 1$ ；若 $x < 0$ ，则 $[x] = x + 1$ ．例 $[1.5] = 0.5$ ， $[- 2] = - 1$ ；已知当 $a > 0$ ， $b < 0$ 时有 $[a] = [b] + 2$ ，则代数式 ${(b - a)}^{2} - 3 (a - b)$ 的值为．

查看试题解析
16. 如图，将连续奇数1，3，5，7，…，排成图表．将十字框上下左右移动，可框住另外五个数，若设中间数为a，则十字框的五个数之和为．

查看试题解析
17. 定义一种对正整数n的“F”运算：①当n为奇数时，结果为 $3 n + 1$ ；②当n为偶数时，结果为 $\frac{n}{2^{k}}$ （其中k是使运算结果为奇数的正整数），并且运算可以重复进行，例如，取 $n = 25$ 时，运算过程如图．若 $n = 34$ ，则第2024次“F运算”的结果是．

查看试题解析
18. 如图所示，在长方形 $A B C D$ 中， $A D = 3 A B$ ，在它内部有三个小正方形，正方形 $A E F G$ 的边长为m，正方形 $G B I H$ 的边长为n，则阴影部分的周长为（用含m，n的代数式表示）．

查看试题解析

三、解答题：本大题10小题，共96分.

19. 计算或者化简：

(1)、 $2 \frac{1}{3} + 6 \frac{3}{5} + (- 2 \frac{1}{3}) + (- 5 \frac{3}{5})$ ；

(2)、 $3 a^{2} - 2 b - 7 a^{2} + 3 b$ ；

(3)、 $- 2^{2} \times [(2 - 8) \div 6] - 18 \div {(- 3)}^{2}$ ；

(4)、 $2 m^{2} - 4 m + 1 - 2 (m^{2} + 2 m - \frac{1}{2})$ ．

查看试题解析
20. 在七年级数学活动课上，有三位同学各拿一张卡片，卡片上分别印有 $A$ ， $B$ ， $C$ 三个代数式，三个代数式如下，其中 $C$ 的代数式是未知的．
$A = - 2 x^{2} - (k - 1) x + 1$
$B = 2 (x^{2} - x + 2)$
$C$

(1)、若 $A$ 为二次二项式，则 $k$ 的值为________；

(2)、在（1）的条件下，若 $C = B - 2 A$ ，求 $C$ ；

(3)、若 $A + B$ 的结果为常数，则这个常数是________，此时 $k$ 的值为________．

查看试题解析
21. 现有甲、乙、丙三种正方形和长方形卡片各若干张，如图1所示（ $a > 1$ ）．小明分别用6张卡片拼出了如图2和图3的两个长方形（不重叠无缝隙），其面积分别为 $S_{1}$ ， $S_{2}$ ．

(1)、请用含a的式子分别表示 $S_{1}$ ， $S_{2}$ ；

(2)、当 $a = 3$ 时，通过计算比较 $S_{1}$ 与 $S_{2}$ 的大小．

查看试题解析
22. 小王在数学学习中发现： $(1 + 2) \div 3 = 1$ ， $(2 + 7) \div 3 = 3$ ， $(3 + 3) \div 3 = 2$ ， $(4 + 5) \div 3 = 3$ ， …而自然数12，27，33，45，……，这样的自然数都能被3整除．
猜想：如果一个自然数的所有数位之和能被3整除，那么这个自然数就能被3整除．并给出了当这个自然数为两位数时的说明如下：
如果一个两位数的十位、个位上的数字分别是a、b，那么记这个两位数为 $\bar{a b}$ ，于是 $\bar{a b} = 10 a + b = 9 a + (a + b)$ ．
而9a能被3整除，因此如果 $a + b$ 能被3整除，那么 $9 a + (a + b)$ 就能被3整除，即 $\bar{a b}$ 能被3整除．
据此回答下列问题：

(1)、用含a、b、c的代数式表示三位数 $\bar{a b c} =$ （其中a是百位数，b是十位数，c是个位数）；

(2)、类比上述的过程，尝试说明：如果一个三位数 $\bar{a b c}$ 的所有数位之和能被9整除，那么这个三位数就能被9整除．

查看试题解析
23. 阅读理解学习：
【阅读材料】一个含有多个字母的代数式中，如果任意交换两个字母的位置，代数式的值都不变，这样的代数式叫做对称式．例如：代数式 $a b c$ 中任意两个字母交换位置，可得到代数 $b a c, a c b, c b a$ ，因为 $a b c = b a c = a c b = c b a$ ，所以 $a b c$ 是对称式；而代数式 $a - b$ 中字母 $a, b$ 交换位谓，得到代数式 $b - a$ ，因为 $a - b$ 与 $b - a$ 不一定相等，所以 $a - b$ 不是对称式．
【理解判断】下列四个代数式中，是对称式的是_______________（填序号即可）；
① $a^{2} + b^{2}$ ；② $a^{2} b$ ；③ $\frac{b}{a}$ ；④ $a + b + c$
【能力提升】
（1）请直接写出一个只含有字母 $x, y$ 的单项式，使该单项式是对称式，且次数为8次；
（2）已知 $A = 2 a^{3} b^{2} - 3 b^{2} c^{2} + \frac{1}{4} a c^{2}, B = 3 a^{3} b^{2} - 4 b^{2} c^{2}$ ，求 $4 A - 3 B$ ，并直接判断所得结果是否为对称式．

查看试题解析
24. 【知识背景】
在学习计算框图时，可以用“”表示数据输入、输出框；用“”表示数据处理和运算框；用“”表示数据判断框（根据条件决定执行两条路径中的某一条）
【尝试解决】
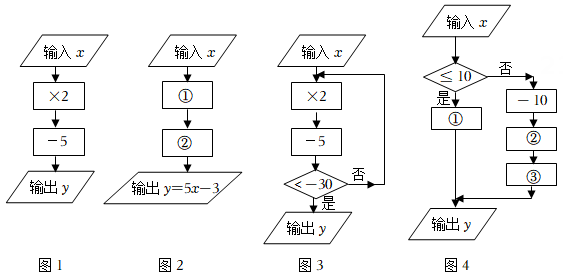
（1）如图1，当输入数 $x = - 1$ 时，输出数 $y =$ ______；
如图2，第①个“”内，应填______；第②个“”内，应填______；
（2）如图3，当输入数 $x = - 2$ 时，请计算出数y的值；
【实际应用】
（3）为鼓励节约用水，某市决定对家庭用水实行“阶梯价”，当每月用水量不超过10吨时（含10吨），以3元/吨的价格收费；当每月用水量超过10吨时，超过部分以4元/吨的价格收费．如图4是小聪设计的一个家庭水费“计算框图”，请把计算框图中①②③方框补充完整．
第①个“”内，应填____________；第②个“”内，应填____________；第③个“”内，应填____________．

查看试题解析
25. 历史上的数学巨人欧拉最先把关于x的代数式用记号f(x)的形式来表示，把x等于某数a时的代数式的值用f(a)来表示，例如当x=-1时，代数式 $f (x) = x^{2} + 3 x - 5$ 的值记为 f(-1)，则 $f (- 1) = (- 1)^{2} +$ 3×(-1)-5=-7。根据上述材料，解答下面的问题：

(1)、已知 $g (x) = - 2 x^{2} + 3 x - 1,$ 求 $g (- \frac{1}{2})$ 的值。

(2)、已知 $f (x) = a x^{5} + b x^{3} + 3 x + c,$ 且 f(0)=-2。
①c= 。
②若 f(1)=-3，求a+b的值。
③若 f(2)=11，求 f(-2)的值。

查看试题解析

26. 如图，一扇窗户，窗框为铝合金材料，上面是由三个大小相等的扇形组成的半圆窗框构成，下面是由两个大小相等的长

2 x

，宽

\frac{1}{2} y

的长方形窗框构成，窗户全部安装玻璃．（本题中

π

取3，长度单位为米）

(1)、一扇这样的窗户一共需要铝合金_________米，需要玻璃________平方米？铝合金窗框宽度忽略不计（用含x，y的式子表示）

(2)、某公司需要购进10扇这样的窗户，在同等质量的前提下，甲、乙两个厂商分别给出如表报价：

	铝合金（元/米）	玻璃（元/平方米）
甲厂商	180	不超过100平方米的部分，90元/平方米，超过100平方米的部分，70元/平方米
乙厂商	200	80元/平方米，每购一平方米玻璃送 $0.1$ 米铝合金

当 $x = 2 ， y = 4$ 时，该公司在哪家厂商购买窗户合算？

查看试题解析

27. 在“生命，幸‘盔’有你”为主题的交通安全宣传教育下，人们骑乘电动自行车佩戴头盔的安全意识不断提高，某电动自行车店计划分别购进30个安全头盔和若干副电动自行车手套，于是店经理联系了批发商，他们之间的对话如下：

(1)、电动自行车店计划购买30个安全头盔和100副手套，若选择方案一共需要花费元．

(2)、电动自行车店计划购买30个安全头盔和a副手套（ $a > 15$ ），
①若选择方案一购买，需要花费 ▲ 元（用含a的代数式表示）；
若选择方案二购买，需要花费 ▲ 元（用含a的代数式表示）；
②假如你是店经理，如何选择购买方案能更省钱？

查看试题解析
28. 艺术节上小德表演了扑克牌魔术，游戏步骤如下：
记牌   小德手里共有54张牌，反复洗牌几次，正面朝下摆放在桌面上，自上而下依次翻开30张牌，摆放方式如图1所示，然后按次序将牌正面朝下倒扣放在桌面上，如图2，再将其摞成一摞，如图3．
抽牌邀请台下一位观众，从剩下的24张牌中任意抽取三张，正面朝上摆放在桌面上，并整理好余下的牌，如图4．
补牌   小德从图4这摞牌中自上而下抽取若干张补放在这三张牌的下方，使每列牌均成为“十全十美牌”．例如，牌面数字是8，则补2张牌，牌面数字是9，则补1张牌，牌面数字是10，则不用补牌（规定J，Q，K和大小王对应的数字均为10），如图5．在补牌时，图4中这摞牌数量不够，则从图3的牌中自上而下拿取进行补放．
合牌   小德将图5中这摞牌不改变顺序，整体放在图3这摞牌的正上方，如图6．
算牌   小德将图4中三张牌的牌面数字相加得， $8 + 10 + 9 = 27$ ，然后请一位观众从图6这摞牌中自上而下抽出第27张牌（不让小德看牌），小德可以准确地说出其牌面数字，很神奇吧！

(1)、在补牌阶段，当抽取的三张牌为8，J，9时（如图5），请把图5中的横线补充完整：                  ；

(2)、小德自己揭秘，其实在记牌阶段他只需要记住图1中的一张牌就可以使魔术成功，请你利用题干中的例子找出小德记住的是第             张牌；

(3)、小德按上述步骤又表演了一次魔术，请运用代数式相关知识解释其中的原理（提示：可以将魔术过程中的某些关键数据设为字母进行推理说明）．

查看试题解析