3.3《 垂径定理》(1)---浙教版数学九年级上册课堂分层训练
试卷更新日期:2025-09-21 类型:同步测试
一、基础应用
-
1. 如图,在中,弦AB的长为8,圆心O到AB的距离 , 则的半径长为( )
 A、4 B、 C、5 D、2. 如图,的半径是3,点O到的距离是2,弦的长是( )
A、4 B、 C、5 D、2. 如图,的半径是3,点O到的距离是2,弦的长是( ) A、 B、 C、 D、3. 如图,的直径 , 是的弦, , 垂足为P,且 , 则的长为( ).
A、 B、 C、 D、3. 如图,的直径 , 是的弦, , 垂足为P,且 , 则的长为( ). A、 B、 C、 D、4. 如图所示,⊙O的半径OB 垂直弦AC 于点D.若AC=16,OD=6,则BD的长为 ( )
A、 B、 C、 D、4. 如图所示,⊙O的半径OB 垂直弦AC 于点D.若AC=16,OD=6,则BD的长为 ( ) A、5 B、4 C、3 D、25. 为了测量一个铁球的直径,将该铁球放入工件槽内,测得的有关数据如图所示(单位:),则该铁球的直径为( )
A、5 B、4 C、3 D、25. 为了测量一个铁球的直径,将该铁球放入工件槽内,测得的有关数据如图所示(单位:),则该铁球的直径为( ) A、 B、 C、 D、6. 一根排水管的截面如图所示,已知排水管的直径为 , 截面圆的圆心到水面的距离为 , 则水面宽为 .
A、 B、 C、 D、6. 一根排水管的截面如图所示,已知排水管的直径为 , 截面圆的圆心到水面的距离为 , 则水面宽为 . 7. 如图所示,已知的半径为10, , , 则线段的长为 .
7. 如图所示,已知的半径为10, , , 则线段的长为 . 8. 如图,在中的半径 , 圆心到弦的距离为 , 则弦的长度为 .
8. 如图,在中的半径 , 圆心到弦的距离为 , 则弦的长度为 .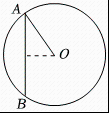 9. 如图,已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D.
9. 如图,已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D. (1)、求证:AC=BD;(2)、若大圆的半径R=10,小圆半径r=8,且圆心O到直线AB的距离为6,求AC的长
(1)、求证:AC=BD;(2)、若大圆的半径R=10,小圆半径r=8,且圆心O到直线AB的距离为6,求AC的长
二、能力提升
-
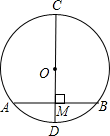
10. 如图,在中,是直径,是弦,于M, , 则的长为.
 11. 如图,点 是以原点 为圆心的圆与 轴的一个交点,直线 交 于 两点,已知弦 的最小值为 2,则点 的坐标为( )
11. 如图,点 是以原点 为圆心的圆与 轴的一个交点,直线 交 于 两点,已知弦 的最小值为 2,则点 的坐标为( ) A、(2,0) B、 C、(3,0) D、12. 如图,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O , 另一边所在直线与半圆相交于点D , E , 量出半径OC=5cm , 弦DE=8cm , 则直尺的宽度为( )
A、(2,0) B、 C、(3,0) D、12. 如图,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O , 另一边所在直线与半圆相交于点D , E , 量出半径OC=5cm , 弦DE=8cm , 则直尺的宽度为( ) A、3cm B、4cm C、5cm D、6cm13. 如图,已知的半径为 , 弦与弦位于圆心的异侧, , , 在上取点 , 连结并延长交于点 . 若 , 则的长为( )
A、3cm B、4cm C、5cm D、6cm13. 如图,已知的半径为 , 弦与弦位于圆心的异侧, , , 在上取点 , 连结并延长交于点 . 若 , 则的长为( ) A、 B、 C、 D、14. 清康熙《新昌县志》载“光霁桥,在县治东北”,今其遗址位于新昌岙桥里,光霁桥为单孔圆弧石拱桥,如图1,已知桥净跨度约6米;矢高约2.5米,如图2,则光霁桥桥拱圆弧的半径为( )
A、 B、 C、 D、14. 清康熙《新昌县志》载“光霁桥,在县治东北”,今其遗址位于新昌岙桥里,光霁桥为单孔圆弧石拱桥,如图1,已知桥净跨度约6米;矢高约2.5米,如图2,则光霁桥桥拱圆弧的半径为( ) A、米 B、3米 C、米 D、米15. 如图,水暖管横截面是圆,半径r=5mm的水暖管有积水(阴影部分),水面的宽度AB 为8 mm,则积水的最大深度 CD(CD<r)是mm.
A、米 B、3米 C、米 D、米15. 如图,水暖管横截面是圆,半径r=5mm的水暖管有积水(阴影部分),水面的宽度AB 为8 mm,则积水的最大深度 CD(CD<r)是mm. 16. 已知的半径为 , 弦 , , , 则、之间的距离为 .17. 如图,⊙O的半径为10,P是弦AB上一动点,若AB=16,则OP的取值范围是
16. 已知的半径为 , 弦 , , , 则、之间的距离为 .17. 如图,⊙O的半径为10,P是弦AB上一动点,若AB=16,则OP的取值范围是 18. 如图,方格纸上每个小正方形的边长均为1个单位长度,点 , , , 在格点(两条网格线的交点叫格点)上,以点为原点建立直角坐标系.
18. 如图,方格纸上每个小正方形的边长均为1个单位长度,点 , , , 在格点(两条网格线的交点叫格点)上,以点为原点建立直角坐标系. (1)、过 , , 三点的圆的圆心坐标为;(2)、请通过计算判断点与的位置关系.19. 如图, , AB交于点C , D , OE是半径,且于点F .
(1)、过 , , 三点的圆的圆心坐标为;(2)、请通过计算判断点与的位置关系.19. 如图, , AB交于点C , D , OE是半径,且于点F . (1)、求证: .(2)、若 , , 求的半径.20. 如图,⊙O的直径AB垂直于弦CD,垂足为E,AE=2,CD=8.
(1)、求证: .(2)、若 , , 求的半径.20. 如图,⊙O的直径AB垂直于弦CD,垂足为E,AE=2,CD=8. (1)、求⊙O的半径长;(2)、连接BC,作OF⊥BC于点F,求OF的长.
(1)、求⊙O的半径长;(2)、连接BC,作OF⊥BC于点F,求OF的长.三、综合拓展
-
21. 如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
 (1)、求圆弧所在的圆的半径r的长;(2)、当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?22. 根据以下情境信息,探索完成任务.
(1)、求圆弧所在的圆的半径r的长;(2)、当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?22. 根据以下情境信息,探索完成任务.公路涵洞改造方案的设计与解决
情境1
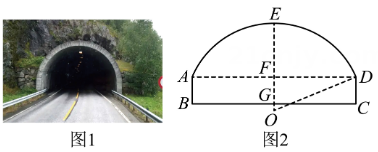
图1是某公路涵洞,图2是其截面示意图,它由圆心在点的劣弧和矩形构成.测得公路宽 , 涵洞直壁高 , 涵洞顶端高出道路()(即).
情境2
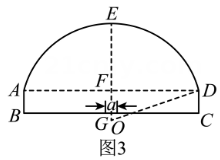
现需对公路进行拓宽,改造成双向隔离车道,并同步拓宽涵洞,中间设置宽为的隔离带,两边为机动车道.如图3,改造后的公路宽 , 涵洞直壁高和涵洞顶端到的距离保持不变.
改造方案
方案一
如图4,将涵洞上半部分劣弧改造成顶点为的抛物线一部分的形式.
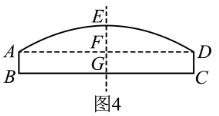
方案二
如图5,将涵洞上半部分劣弧改造成仍为劣弧的形式
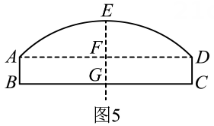
问题解决
任务1
按方案一改造
以点为坐标原点,所在直线为轴建立平面直角坐标系,求抛物线的函数表达式.
任务2
按方案二改造
求涵洞上半部分劣弧所在圆的半径.
任务3
隔离带最大宽度的确定
要使高 , 宽的货运车能通过此公路涵洞,分别求出两种改造方案下的最大值( , , 结果精确到).