相关试卷
-
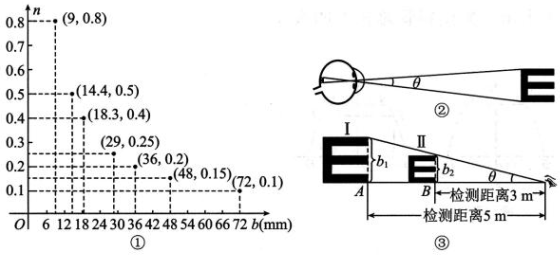
1、 视力表中蕴含着很多数学知识，如：每个“E”形图都是正方形结构，同一行的“E”是全等图形且对应着同一个视力值，不同的检测距离需要不同的视力表.
素材1 国际通用的视力表以5m 为检测距离，任选视力表中7个视力值n，测得对应行的“E”形图边长b(mm)，在平面直角坐标系中描点，如图 R8-1①.
⑴探究1 检测距离为5m 时，归纳n与b 的关系式，并求视力值1.2所对应行的“E”形图边长.
素材2 图②为视网膜成像示意图，在检测视力时，眼睛能看清最小“E”形图所成的角叫做分辨视角θ.视力值n与分辨视角θ(分)的对应关系近似满足
⑵探究2 当n≥1.0时，属于正常视力，根据函数增减性写出对应的分辨视角θ的范围.
素材3 如图③，当θ确定时，在A处用边长为b1的Ⅰ号“E”测得的视力与在B处用边长为b2的Ⅱ号“E”测得的视力相同.
⑶探究3 若检测距离为3m，求视力值1.2所对应行的“E”形图边长.
-
2、 如图①是某一遮阳篷支架从闭合到完全展开的过程，当遮阳篷支架完全闭合时，支架的若干支杆可看作共线.图②是遮阳篷支架完全展开时的示意图，支杆MN固定在垂直于地面的墙壁上，支杆CE与水平地面平行，且G，F，B三点共线，在支架展开过程中，四边形ABCD始终是平行四边形，展开时∠GHB=90°.
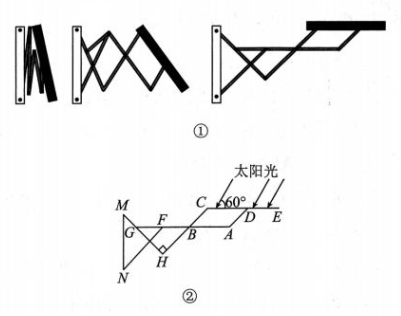(1)、若遮阳篷完全展开时，CE长2米，在与水平地面呈60°的太阳光照射下，CE在地面的影子有米(影子完全落在地面上)；(2)、求长支杆与短支杆的长度比(即CE 与AD 的长度比). -
3、 马家窑文化以发达的彩陶著称于世，其陶质坚固，器表细腻，红、黑、白、彩共用，彩绘线条流畅细致，图案繁缛多变，形成了绚丽典雅的艺术风格，创造了一大批令人惊叹的彩陶艺术精品，体现了古代劳动人民的智慧.如图①的彩陶纹样呈现的是三等分圆周，古人用等边三角形三点定位的方法确定圆周的三等分点，这种方法和下面三等分圆周的方法相通.如图②，已知⊙O和圆上一点 M.作法如下：
①以点 M为圆心，OM长为半径，作弧交⊙O于A，B两点；
②延长MO交⊙O于点C；
即点A，B，C将⊙O的圆周三等分.
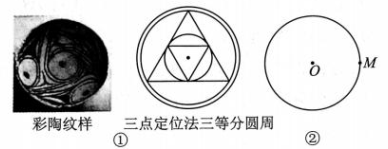(1)、请你依据以上步骤，用不带刻度的直尺和圆规在图②中将⊙O的圆周三等分(保留作图痕迹，不写作法)；(2)、根据(1)画出的图形，连结AB，AC，BC.若⊙O的半径为 2 cm，则△ABC的周长为cm. -
4、某临街商铺想做一款落地窗以展示商品，为防止商品久晒受损，需保证冬至日正午时分太阳光不能照进落地窗.如图，已有的遮阳棚AB=130 cm，遮阳棚前段下摆的自然垂直长度 BC=40 cm，遮阳棚的固定高度AD=240cm，sin∠BAD=
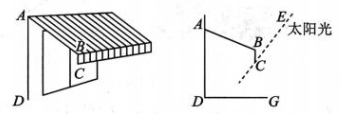(1)、求遮阳棚上的点 B到墙面AD 的距离；(2)、冬至日正午时，该商铺所在地区的太阳的高度角约是53°(光线 EC与地面的夹角)，请通过计算判断该商铺的落地窗方案是否可行.(参考数据： -
5、 如图①为我们常见的马扎，马扎上层是可以折叠但不能伸缩的帆布，图②是马扎撑开后的侧面示意图，其中腿AB 和 CD 的长度相等，O是它们的中点，AB=60 cm，AD=41 cm，当有人坐在马扎上时，马扎侧面示意图变成图③(假设AE与 DE都是线段)，且AE=DE，点 E离地面BC的距离即马扎实际支撑的高度.若某人坐在马扎上时测得∠AOD=83.6°，他要求实际支撑高度为40 cm，则这款马扎能否符合他的要求?
(参考数据：
-
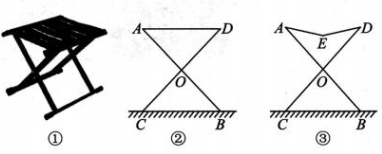
6、 如图①是瓦片做成的窗花，可以从中分离出一朵“花”的图案，如图②，它是由八片相同的瓦片组成的，其中间四片“对扣”，外围截面恰好抽象成一个圆，如图③，A，B，C，D表示瓦片的交接点.
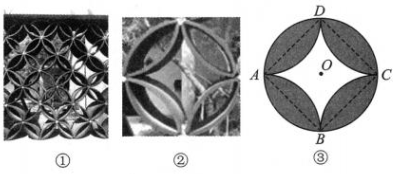(1)、判断四边形ABCD的形状，并说明理由；(2)、若AB=20cm，求图③中阴影部分的面积(结果保留π). -
7、 如图，粮库用传送带传送粮袋，大转动轮的半径为 10 cm，传送带与水平面成30°角.假设传送带与转动轮之间无滑动，当大转动轮转 140°时，传送带上点 A处的粮袋上升的高度是多少?(传送带厚度忽略不计)
-
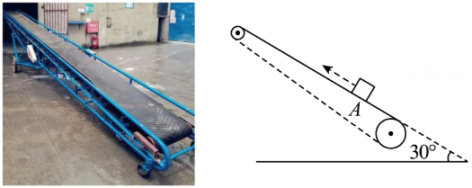
8、 如图，ED为一条宽为4米的河，河的西岸建有一道防洪堤，防洪堤与东岸的高度差为3米(即CE=3米)，因为施工需要，现准备将东岸的泥沙通过滑轨送到西岸的防洪堤上，防洪堤上已经建好一座固定滑轨一端的钢架，现准备在东岸找一个点 P 作为另一端的固定点，已知吊篮的截面为直径为1米的半圆(直径MN=1米)，绳子QM=QN=1.3米，钢架高度2.2米(AB=2.2米)，距离防洪堤边缘为0.5米(BC=0.5米).
(1)、西岸边缘点 C 与东岸边缘点 D 之间的距离为米；(2)、滑轨在运送货物时保持笔直，要想做到运输过程中吊篮一定不会碰到点C，则DP 的长度应大于米. -
9、 如图①为《天工开物》记载的用于春(chōng)捣谷物的工具——“碓(duì)”的结构简图，图②为其平面示意图.已知AB⊥CD 于点 B，AB 与水平线 l相交于点O，OE⊥l. 若 BC= 4 dm，OB = 12 dm，∠BOE=60°，则点 C 到水平线 l 的距离 CF为dm(结果用含根号的式子表示).
-
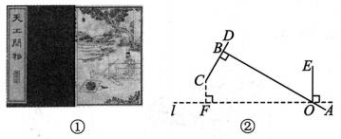
10、综合与实践
数学实践活动，是一种非常有效的学习方式.通过活动可以激发我们的学习兴趣，提高动手动脑能力，拓展思维空间，丰富数学体验，让我们一起动手来折一折、转一转，体会活动带给我们的乐趣.
折一折：将正方形纸片 ABCD 折叠，使边AB，AD 都落在对角线AC 上，展开得折痕AE，AF，连结EF，如图①.
(1)、∠EAF=°，写出图中两个等腰三角形：(不添加辅助线和字母)；转一转：将图①中的∠EAF 绕点 A 旋转，使它的两边分别交边 BC，CD 于点 P，Q，连结PQ，如图②.(2)、线段 BP，PQ，DQ 之间的数量关系为；(3)、连结正方形 ABCD 的对角线 BD，若图②中的∠PAQ的边AP，AQ分别交对角线BD于点M，N，如图③，求 的值. -
11、 如图，在△ABC 中，∠BAC=45°，AD⊥BC，垂足为 D.若BD=6，CD=4，求高线AD的长.
-
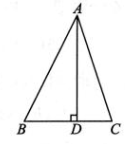
12、如图，已知反比例函数 的图象经过点A(3，4)，在该图象上找一点 P，使∠POA=45°，则点 P 的坐标为 .
-
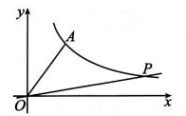
13、如图，在平面直角坐标系中，一次函数 y =2x-2 的图象分别交x轴、y轴于点A，B，直线 BC与x 轴正半轴交于点C.若∠ABC=45°，则直线 BC的函数表达式是( )
A、y=3x-2 B、 C、 D、 -
14、 如图，在矩形ABCD 中，AB=14，E 是BC边上一点，且 BE=6，连结 AE，AC.若∠CAE=45°，则CE的长为 ( )
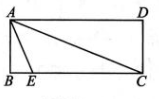A、20 B、29 C、 D、 -
15、题目：“如图 ，∠B=45°，BC=2，在射线 BM上取一点A，设AC=d，若对于d的一个数值，只能作出唯一一个△ABC，求d的取值范围.”对于其答案，甲答：d≥2，乙答：d=1.6，丙答： 则正确的是( )
A、只有甲答得对 B、甲、丙的答案合在一起才完整 C、甲、乙的答案合在一起才完整 D、三人的答案合在一起才完整 -
16、如图，△ABC为等腰直角三角形，∠BAC=90°，AB=AC，D 是AC上一点，CE⊥BD交直线 BD 于点E，且∠AEB=45°.若BE=7，AE=3 ， F为BC的中点，连结EF，则EF的长为 ( )
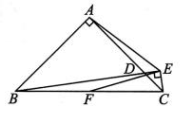A、 B、 C、 D、 -
17、如图，在△ABC中，分别过点 B，A 作 BD⊥AC于点 D，AE⊥BC于点 E，BD，AE交于点 F.若∠BAC=45°，AD=5，CD=2，则线段 BF的长度为 ( )
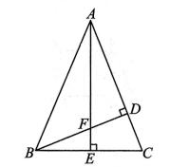A、2 B、 C、3 D、 -
18、
(1)、如图①，已知 OC 是∠AOB 的平分线，P是OC上任意一点，点D，E分别在边 OA，OB 上，连 结 PD，PE，∠AOB +∠DPE=180°.若∠AOB=60°，OD+OE= ， 则OP的长为；(2)、如图②，在▱ABCD 中，∠ABC=60°，BE平分∠ABC交AD 于点E，连结CE，将CE 绕点 E 旋转，当点 C 的对应点 F 落在边AB 上时，若 求四边形BCEF的面积. -
19、 在△ABC中，AB=AC，∠BAC=90°，BD平分∠ABC交AC于点 D.
(1)、如图①，F 为 BC 上一点，连结 AF交BD于点E.若AB=BF，求证：BD垂直平分AF；(2)、如图②，CE⊥BD，垂足 E 在 BD 的延长线上，试判断线段CE，BD 之间的数量关系，并说明理由；(3)、如图③，F 为 BC 上一点，∠EFC= ∠ABC，CE⊥EF，垂足为E，EF与AC 交于点M.直接写出线段CE，FM之间的数量关系. -
20、 如图，四边形 ABCD为平行四边形，∠BAD的平分线AF交CD 于点E，交 BC的延长线于点 F，连结 BE.若 BE⊥AF，EF= ， 则AB的长为.
