第十四章《全等三角形》提升卷—沪科版数学八(上)单元分层测
试卷更新日期:2025-09-21 类型:单元试卷
一、选择题:本大题共12小题,每小题3分,在每小题给出的四个选项中,只有一个是正确的.每小题选对得3分,选错、不选或多选,均不得分.
-
1. 如图,已知 , , 添加下列条件仍不能判定的是( )
 A、 B、 C、 D、2. 如图,点B、D、E、C在同一直线上,△ABD≌△ACE,∠AEC=100°,则∠DAE=( )
A、 B、 C、 D、2. 如图,点B、D、E、C在同一直线上,△ABD≌△ACE,∠AEC=100°,则∠DAE=( )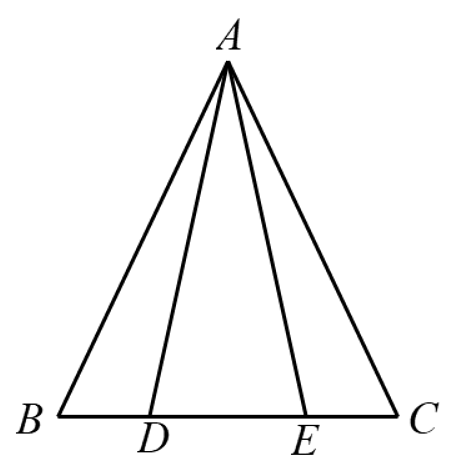 A、10° B、20° C、30° D、80°3. 如图, , 记 , 当 时, 与 之间的数量关系为( )
A、10° B、20° C、30° D、80°3. 如图, , 记 , 当 时, 与 之间的数量关系为( ) A、 B、 C、 D、4. 在如图所示的5×5方格中,每个小方格都是边长为1的正方形,是格点三角形(即顶点恰好是正方形的顶点),则与有一条公共边且全等的所有格点三角形的个数是( )
A、 B、 C、 D、4. 在如图所示的5×5方格中,每个小方格都是边长为1的正方形,是格点三角形(即顶点恰好是正方形的顶点),则与有一条公共边且全等的所有格点三角形的个数是( ) A、1 B、2 C、3 D、45. 如图是一款路灯及其平面示意图,已知AB=AD,CF=CG,B,D分别为 CF,CG 的中点, ∠ABF = 122°,∠BAE=59°,则∠ACD 的度数为 ( )
A、1 B、2 C、3 D、45. 如图是一款路灯及其平面示意图,已知AB=AD,CF=CG,B,D分别为 CF,CG 的中点, ∠ABF = 122°,∠BAE=59°,则∠ACD 的度数为 ( )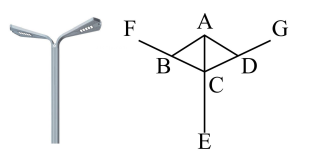 A、58° B、59° C、63° D、70°6. 如图是一个正方形网格,每个小正方形的边长相等,我们把该网格中正方形的顶点称之为“好点”,△ABC的三个顶点都在这个正方形网格的“好点”上,在这个正方形网格图中找一个“好点”D(点D与点A不重合),使得以点D,B,C为顶点的三角形与△ABC全等,则这样的“好点”D的个数为( )
A、58° B、59° C、63° D、70°6. 如图是一个正方形网格,每个小正方形的边长相等,我们把该网格中正方形的顶点称之为“好点”,△ABC的三个顶点都在这个正方形网格的“好点”上,在这个正方形网格图中找一个“好点”D(点D与点A不重合),使得以点D,B,C为顶点的三角形与△ABC全等,则这样的“好点”D的个数为( ) A、1 B、2 C、3 D、47. 如图,在中, , 和的平分线、相交于点 , 交于点 , 交于点 , 若已知周长为 , , , 则长为( )
A、1 B、2 C、3 D、47. 如图,在中, , 和的平分线、相交于点 , 交于点 , 交于点 , 若已知周长为 , , , 则长为( )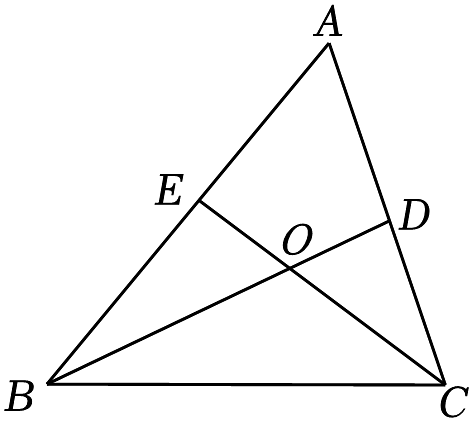 A、 B、 C、 D、48. 如图, , . 给出下列条件:①;② , ③ , ④ . 这四个条件中再选一个使 , 符合条件的有( )
A、 B、 C、 D、48. 如图, , . 给出下列条件:①;② , ③ , ④ . 这四个条件中再选一个使 , 符合条件的有( ) A、1个 B、2个 C、3个 D、4个9. 用三角尺可以按照下面的方法画∠AOB的角平分线:在OA、OB上分别取点M、N,使OM=ON;再分别过点M、N画OA、OB的垂线,这两条垂线相交于点P,画射线OP(如图),则射线OP平分∠AOB,以上画角平分线时,用到的三角形全等的判定方法是( )
A、1个 B、2个 C、3个 D、4个9. 用三角尺可以按照下面的方法画∠AOB的角平分线:在OA、OB上分别取点M、N,使OM=ON;再分别过点M、N画OA、OB的垂线,这两条垂线相交于点P,画射线OP(如图),则射线OP平分∠AOB,以上画角平分线时,用到的三角形全等的判定方法是( ) A、SSS B、SAS C、HL D、ASA10. 如图为个边长相等的正方形的组合图形,则( )
A、SSS B、SAS C、HL D、ASA10. 如图为个边长相等的正方形的组合图形,则( ) A、 B、 C、 D、11. 如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当时间t为( )s时,能够使△BPE与△CQP全等.
A、 B、 C、 D、11. 如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当时间t为( )s时,能够使△BPE与△CQP全等. A、1 B、1或4 C、1或2 D、312. 如图,在平面直角坐标系中,直线相交于点 , . 下列四个说法:
A、1 B、1或4 C、1或2 D、312. 如图,在平面直角坐标系中,直线相交于点 , . 下列四个说法:;
为线段中点;
;
点的坐标为 . 其中正确说法的个数是( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题:本大题共4小题,每小题4分,共16分.只要求填出最后结果.
-
13. 一个三角形的三条边的长分别是 , , , 另一个三角形的三条边的长分别是 , , , 若这两个三角形全等,则的值是 .14. 如图,在中,是高, , , 在边上取点 , 连接 , , 若 , , 则 .
 15. 如图,在中, , , 以BC所在直线为x轴,过点A作BC的垂线为y轴建立直角坐标系,D , E分别为线段AO和线段AC上一动点,且 . 当的值最小时,点E的坐标为 .
15. 如图,在中, , , 以BC所在直线为x轴,过点A作BC的垂线为y轴建立直角坐标系,D , E分别为线段AO和线段AC上一动点,且 . 当的值最小时,点E的坐标为 . 16. 为改善照明环境,小区物业在一号楼底部和二号楼顶部分别安装了照射灯(灯的高度忽略不计),如图,已知A处地面灯恰好照射到二号楼顶部灯B处,B灯恰好照射到一号楼顶部C处,且两盏灯的光线与地平面的夹角相等,若一号楼AC的高为44.8m,则二号楼BD的高为
16. 为改善照明环境,小区物业在一号楼底部和二号楼顶部分别安装了照射灯(灯的高度忽略不计),如图,已知A处地面灯恰好照射到二号楼顶部灯B处,B灯恰好照射到一号楼顶部C处,且两盏灯的光线与地平面的夹角相等,若一号楼AC的高为44.8m,则二号楼BD的高为
三、解答题:本大题共7小题,共68分.
-
17. 如图:小刚站在河边的点处,在河的对面(小刚的正北方向)的处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树处,接着再向前走了30步到达处,然后他左转向正南方向直行,当小刚看到电线塔、树与自己现处的位置在一条直线时,他从到走了80步.
 (1)、根据题意,画出示意图;(2)、如果小刚一步大约米,估计小刚在点处时他与处电线塔的距离,并说明理由.18. 如图,如图,点P在AB上,∠1=∠2, ∠3=∠4.
(1)、根据题意,画出示意图;(2)、如果小刚一步大约米,估计小刚在点处时他与处电线塔的距离,并说明理由.18. 如图,如图,点P在AB上,∠1=∠2, ∠3=∠4.
(1)求证: △BDP≌△BCP;
(2)求证:AD=AC.
19. 如图在 , 中, , , , 点C,D,E三点在同一条直线上,连接 , 求证: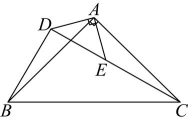 (1)、;(2)、试猜想 , 有何特殊的位置关系,并说明理由.20. 如图, A B∥C D , AC = DC ,____,求证:
(1)、;(2)、试猜想 , 有何特殊的位置关系,并说明理由.20. 如图, A B∥C D , AC = DC ,____,求证: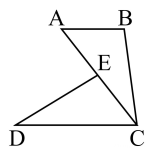 (1)、请从①∠AED=∠BCD,②DE=BC,③DC-AE=AB 中选择一个适当的条件填入横线中,使命题成立.你的选择是(只需填一个序号即可);(2)、根据(1)中的选择给出证明.21. 某中学八年级(5)班的学生到野外进行数学活动,为了测量一池塘两端A、B之间的距离,同学们设计了如下两种方案:
(1)、请从①∠AED=∠BCD,②DE=BC,③DC-AE=AB 中选择一个适当的条件填入横线中,使命题成立.你的选择是(只需填一个序号即可);(2)、根据(1)中的选择给出证明.21. 某中学八年级(5)班的学生到野外进行数学活动,为了测量一池塘两端A、B之间的距离,同学们设计了如下两种方案:
方案1:如图(1),先在平地上取一个可以直接到达A、B的点C,连接AC并延长AC至点D,连接BC并延长至点E,使DC=AC,EC=BC,最后量出DE的距离就是AB的长.
方案2:如图(2),过点B作AB的垂线BF,在BF上取C、D两点,使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB间的距离
问:(1)方案1是否可行?并说明理由;
(2)方案2是否可行?并说明理由;
(3)小明说:“在方案2中,并不一定需要BF⊥AB,DE⊥BF,将“BF⊥AB,DE⊥BF”换成条 也可以.”你认为小明的说法正确吗?如果正确的话,请你把小明所说的条件补上.
22. 如图1,在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 直线与轴交于点 , 与轴交于点 , 满足;与直线交于点 , 且点的横坐标为 . (1)、求 , 的值(2)、求四边形的面积(3)、如图2,点是线段上的一动点,过点作轴的平行线交直线于点 , 连接、;若 , 求点的坐标;23. 三个等角的顶点在同一条直线上,称一线三等角模型(角度有锐角、直角、钝角,若为直角,则又称一线三垂直模型),解决此模型问题的一般方法是利用三等角关系找全等三角形所需角的相等条件,利用全等三角形解决问题.
(1)、求 , 的值(2)、求四边形的面积(3)、如图2,点是线段上的一动点,过点作轴的平行线交直线于点 , 连接、;若 , 求点的坐标;23. 三个等角的顶点在同一条直线上,称一线三等角模型(角度有锐角、直角、钝角,若为直角,则又称一线三垂直模型),解决此模型问题的一般方法是利用三等角关系找全等三角形所需角的相等条件,利用全等三角形解决问题.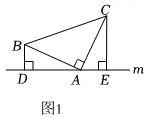
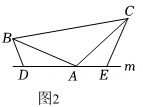
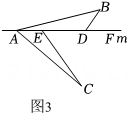 (1)、如图1,在中, , , 直线经过点 , 直线 , 直线 , 垂足分别为、 . 求证: .(2)、如图2,将(1)中的条件改为:在中, , 、、三点都在直线上,并且有 , 其中为任意锐角或钝角,那么结论是否仍成立?若成立,请你给出证明;若不成立,请说明理由.(3)、如图3,将(1)中的条件改为: , 、、三点都在直线上,且有 , 其中为任意锐角,那么结论是否仍成立?若成立,请你给出证明;若不成立,请说明理由.
(1)、如图1,在中, , , 直线经过点 , 直线 , 直线 , 垂足分别为、 . 求证: .(2)、如图2,将(1)中的条件改为:在中, , 、、三点都在直线上,并且有 , 其中为任意锐角或钝角,那么结论是否仍成立?若成立,请你给出证明;若不成立,请说明理由.(3)、如图3,将(1)中的条件改为: , 、、三点都在直线上,且有 , 其中为任意锐角,那么结论是否仍成立?若成立,请你给出证明;若不成立,请说明理由.