相关试卷

1、如图，在△ABC中，AB=5， BC=3，AC=4，点 P 从点 A 出发沿AB 运动到点 B，作如图所示的主从联动-直线Rt△PQC，且∠CPQ = 30°，∠Q = 90°，则△PQC的外心运动的路径长为， BQ的最小值为.

查看解析
2、如图，等边三角形 ABC内接于⊙O，BC=6，D为CA上一动点，过点 B 作射线DO的垂线，垂足为 E.

(1)、⊙O的半径为；

(2)、当点 D 由点C 沿CA运动到点A 时，点 E的运动路径长为.

查看解析
3、如图，点 A，B的坐标分别为(2，0)，(0，2)，C为坐标平面内一点，BC=1，M为线段AC的中点，连结OM，则OM的最大值为( )

A、 $\sqrt{2} + 1$ B、 $\sqrt{2} + \frac{1}{2}$ C、 $2 \sqrt{2} + 1$ D、 $2 \sqrt{2} - \frac{1}{2}$

查看解析
4、如图，在平面直角坐标系中，点A(4，0)，B(0，-3)，以点 B为圆心，2为半径的⊙B上有一动点 P，连结 AP.若C为AP的中点，连结 OC，则OC 的最小值为

查看解析
5、如图，在矩形ABCD 中，AB=5，BC= $5 \sqrt{3}$ ，点 P 在线段BC 上运动(含 B，C两点)，连结AP，以点 A为中心，将线段 AP 逆时针旋转60°得到 AQ，连结 DQ，则线段 DQ的最小值为( )

A、 $\frac{5}{2}$ B、 $5 \sqrt{2}$ C、 $\frac{5 \sqrt{3}}{3}$ D、3

查看解析
6、如图，在正方形ABCD中，AB=4，E，F分别是CD，BC边上的动点，且始终满足 DE=CF，DF 与 AE 相交于点 G.以AG为斜边在AG下方作等腰直角三角形 AHG，使得∠AHG=90°，连结BH，则BH的最小值为 ( )

A、 $2 \sqrt{5} - 2$ B、 $2 \sqrt{5} + 2$ C、 $\sqrt{10} - \sqrt{2}$ D、 $\sqrt{10} + \sqrt{2}$

查看解析
7、如图，在平面直角坐标系中，Q是直线 $y = - \frac{1}{2} x + 2$ 上的一个动点，将点Q绕点P(1，0)顺时针旋转 90°，得到点Q'，连结OQ'，则OQ'的最小值为( )

A、 $\frac{4 \sqrt{5}}{5}$ B、 $\sqrt{5}$ C、 $\frac{5 \sqrt{2}}{3}$ D、 $\frac{6 \sqrt{5}}{5}$

查看解析
8、如图，AB 是⊙O 的直径，AB=4，C是上半圆. $\hat{A B}$ 的中点，D是下半圆 $\hat{A B}$ 上一个动点，过点 A 作 CD 的垂线，垂足为E，则点 D 从点 A 运动到点 B 的过程中，点E运动的路径长是( )

A、π B、 $\sqrt{2}$ C、2π D、2 $\sqrt{2}$

查看解析
9、如图，已知两条平行线l₁ ， l₂ ， A是l₁上的定点，AB⊥l₂于点B，C，D分别是l₁ ， l₂上的动点，且满足AC=BD，连结CD 交线段 AB 于点 E，BH⊥CD 于点H，则当∠BAH 最大时，sin∠BAH 的值为

查看解析
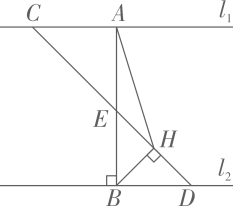
10、如图，在半径为4 的⊙O中，CD 为直径，弦AB⊥CD 且过半径OD 的中点，E 为⊙O上一动点，CF⊥AE 于点 F.当点 E 从点B 出发顺时针运动到点 D 时，点F 所经过的路径长为.

查看解析
11、如图，在正方形ABCD中，以AB为直径作半圆O，P 为半圆上一点，连结AP 并延长交 BC 边于点 E，连结 BP 并延长交CD 边于点 F，连结CP.

(1)、求证：AE=BF；

(2)、当AB=1时，求CP 的最小值；

(3)、若CP=CF，求 BE： BC 的值.

查看解析
12、已知 Rt△ABC中，∠B=90°，∠A=30°，BC=1，含 30°角的Rt△DEF的三个顶点分别在 Rt△ABC 的三边上，且直角顶点D 在斜边AC上，则CD 的长为.

查看解析
13、如图，在△ABC 中，AB=AC=5，BC=6，D是BC 的中点，E 为AB 上一动点.若点 B 关于 DE 的对称点 B'在△ABC 内(不含△ABC的边上)，则 BE长的取值范围为.

查看解析
14、构造运用(图中无圆)

(1)、如图 ①，在边长为2 的菱形 ABCD中，∠A=60°，M 是AD 边的中点，N 是AB边上一动点，将△AMN 沿 MN 所在的直线翻折得到△A'MN，连结 A'C，请求出 A'C 长度的最小值.
解：由折叠知 $A^{'} M = A M ，$ 又 M 是 AD 的中点，可得. $M A^{'} = M A = M D ，$ 故点 A'在以AD为直径的圆上.如图②，以点 M 为圆心，MA为半径画⊙M，过点 M 作MH⊥CD，垂足为H.(请继续完成解题过程)

(2)、如图，在▱ABCD 中，∠C=120°，AB=8，BC=10，E为边 CD 的中点，F 为边 AD 上一动点，将△DEF 沿 EF 翻折得△D'EF，连结 AD'，BD'，则△ABD'面积的最小值为.

查看解析
15、如图，在 Rt△ABC 中，∠ACB=90°，∠BAC=30°，BC=2，E 是斜边 AB 的中点，把 Rt△ABC绕点 A 顺时针旋转得 Rt△AFD，点C，B旋转后的对应点分别是点 D，F，连结CF，EF，CE.在旋转的过程中，△CEF 面积的最大值是.

查看解析
16、如图，正方形 ABCD 的边长为3，将长为2 $\sqrt{3}$ 的线段 QF 的两端点放在正方形相邻的两边上同时滑动.如果点 Q 从点 A 出发，在AB上滑动，同时点 F 在 BC 上滑动，当点F到达点 C 时，运动停止，那么在这个过程中，线段 QF 的中点M 所经过的路线长为( )

A、 $\sqrt{62}$ B、 $\frac{3 \sqrt{2} - \sqrt{6}}{2}$ C、 $\sqrt{36}$ D、 $\frac{\sqrt{3}}{3} π$

查看解析
17、如图，在四边形 ABCD 中，DC∥AB，BC=1，AB=AC=AD=2，则 BD 的长为

查看解析
18、【项目式学习】
项目主题：设计落地窗的遮阳篷.
项目背景：小明家的窗户朝南，窗户的高度AB=2m，为了遮挡太阳光，小明做了以下遮阳篷的设计方案，请根据不同设计方案完成以下任务.
方案 1：直角形遮阳篷
如图，小明设计的第一个方案为直角形遮阳篷BCD，点C在AB 的延长线上，CD⊥AC.

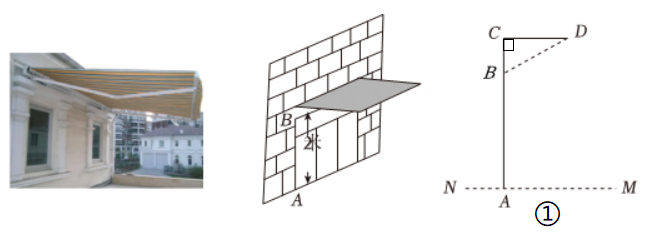(1)、若BC=0.5m，CD=1m，则支撑杆BD=m.

(2)、小明发现上述方案不能很好发挥遮阳作用，如图，他观察到此地一年中的正午时刻，太阳光与地平面的最小夹角为α，最大夹角为β.小明查阅资料，计算出 $t a n α = \frac{1}{3} ， t a n β = \frac{4}{3} ，$ 为了让遮阳篷既能最大限度地使冬天温暖的阳光射入室内(太阳光与 BD 平行)，又能最大限度地遮挡夏天炎热的阳光(太阳光与AD平行)，请求出图②中BC，CD的长度.

(3)、方案2：抛物线形遮阳篷
如图，为了美观及实用性，小明在(2)的基础上将CD 边改为抛物线形可伸缩的遮阳篷(F 为抛物线的顶点，DF段可伸缩)，且∠CFD=90°，BC，CD的长保持不变.若以C为原点，CD方向为x轴，BC方向为y轴.
①求该二次函数的表达式；
②若某时刻太阳光与水平地面的夹角θ的正切值 $t a n θ = \frac{2}{3} ，$ 为使阳光最大限度地射入室内，求遮阳篷点 D上升高度的最小值(即点 D'到CD 的距离).

查看解析
19、【项目式学习】
项目主题：守护生命，“数”说安全.
项目背景：随着社会的发展，安全问题变得日益重要.某校为了提高学生的安全意识，开展以“守护生命，‘数’说安全”为主题的项目式学习活动.创新小组通过考察测量、模拟探究和成果迁移等环节，开展地下弯道对通行车辆长度的限制研究.

(1)、任务一：考察测量
如图①，创新小组所选取弯道的内、外侧均为直角，道路宽均为 4m，则AB=m.

(2)、任务二：模拟探究
如果汽车在行驶中与弯道内、外侧均无接触，则可安全通过.
创新小组用线段模拟汽车通过宽度相同的直角弯道，探究发现：
①当CD<2AB时(如图①)，线段CD能通过直角弯道；
②当CD=2AB时，必然存在线段CD的中点E 与点B 重合的情况，线段 CD 恰好不能通过直角弯道(如图②).此时，∠ADC的度数是；
③当CD>2AB时，线段CD不能通过直角弯道.

(3)、如图③，创新小组用矩形 PQMN模拟汽车通过宽均为4m 的直角弯道，发现当PQ的中点E与点B重合，且PQ⊥AB时，矩形 PQMN恰好不能通过该弯道.若PQ=a m，PN=2m，且矩形PQMN能通过该直角弯道，求a的最大整数值.

(4)、任务三：成果迁移
如图④，某弯道外侧形状可近似看成反比例函数 $y = \frac{k}{x} (x⟩ 0)$ 的图象，其对称轴交图象于点
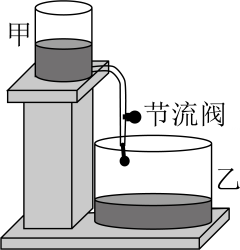
A.弯道内侧的顶点 B在射线OA 上，两边分别与x轴，y轴平行，( $O A = 2 m ， A B = 4 \sqrt{2} m .$ 创新小组探究发现通过该弯道的原理与通过直角弯道类似.有一辆长为 bm，宽为2m的汽车需要安全通过该弯道，则b的最大整数值为.(参考数据： $\sqrt{2} \approx 1.4 ， \sqrt{3} \approx 1.7 ， \sqrt{5} \approx 2.2 ， \sqrt{7} \approx 2.6)$

查看解析
20、【问题背景】“刻漏”是我国古代的一种利用水流计时的工具.综合实践小组准备用甲、乙两个透明的竖直放置的容器和一根带节流阀(控制水的流速大小)的软管制作简易计时装置(如图).

流水时间 t/ min
0
10
20
30
40
水面高度 h/cm
(观察值)
30
29
28.1
27
25.8

(1)、【实验操作】综合实践小组设计了如下的实验：先在甲容器里加满水，此时水面高度为30 cm，开始放水后每隔10 min观察一次甲容器中的水面高度，获得的数据如下表：
任务1：分别计算表中每隔10 min水面高度观察值的变化量.

(2)、【建立模型】小组讨论发现：‘“t=0，h=30”是初始状态下的准确数据，水面高度值的变化不均匀，但可以用一次函数近似地刻画水面高度h与流水时间t的关系.
任务2：利用t=0时，h=30；t=10时，h=29这两组数据求水面高度h与流水时间t的函数表达式.

(3)、【反思优化】经检验，发现有两组表中观察值不满足任务2中求出的函数表达式，存在偏差，小组决定优化函数表达式，减少偏差.通过查阅资料后知道：t为表中数据时，根据表达式求出所对应的函数值，计算这些函数值与对应h的观察值之差的平方和，记为w；ω越小，偏差越小.
任务3：
①计算任务2得到的函数表达式的w值；
②请确定图象经过点(0，30)的一次函数表达式，使得w的值最小.

(4)、【设计刻度】得到优化的函数表达式后，综合实践小组决定在甲容器外壁设计刻度，通过刻度直接读取时间.
任务4：请你简要写出时间刻度的设计方案.

查看解析

上一页 334 335 336 337 338 下一页跳转