相关试卷
- 冀教版数学八年级上学期期中仿真模拟试卷一(范围:12-14章)
- 第四章《一元一次方程》提升卷—苏科版数学七(上)单元测
- 第三章《代数式》提升卷—苏科版数学七(上)单元测
- 第三章《代数式》基础卷—苏科版数学七(上)单元测
- 第十五章《轴对称图形和等腰三角形》提升卷—沪科版数学八(上)单元分层测
- 第十五章《轴对称图形和等腰三角形》基础卷—沪科版数学八(上)单元分层测
- 第十四章《全等三角形》提升卷—沪科版数学八(上)单元分层测
- 第十四章《全等三角形》基础卷—沪科版数学八(上)单元分层测
- 第十三章《三角形中的边角关系、命题与证明》提升卷—沪科版数学八(上)单元分层测
- 第十三章《三角形中的边角关系、命题与证明》基础卷—沪科版数学八(上)单元分层测
-
1、 若实数x满足 , 则的值为( )A、2025 B、2026 C、2027 D、2028
-
2、 在同一平面内,有三条不重合的直线a , b , c , ( )A、若 , , 则 B、若 , , 则 C、若 , , 则 D、若 , , 则
-
3、 下列等式变形中,正确的是( )A、 B、 C、 D、
-
4、 当时,下列代数式的值最小的是( )A、 B、 C、 D、
-
5、 若是二元一次方程的一个解,则( )A、0 B、1 C、2 D、3
-
6、 要使分式有意义,则x的取值需满足( )A、 B、 C、或 D、且
-
7、 要了解某校学生每周体育锻炼的时间,下列选取调查对象的方式最合适的是( )A、随机选取一个体育队的学生 B、在全校学生中随机选取100人 C、随机选取一个班的学生 D、在全校男生中随机选取100人
-
8、【感悟】如图1,是的高线, , 若 , , 求的长.
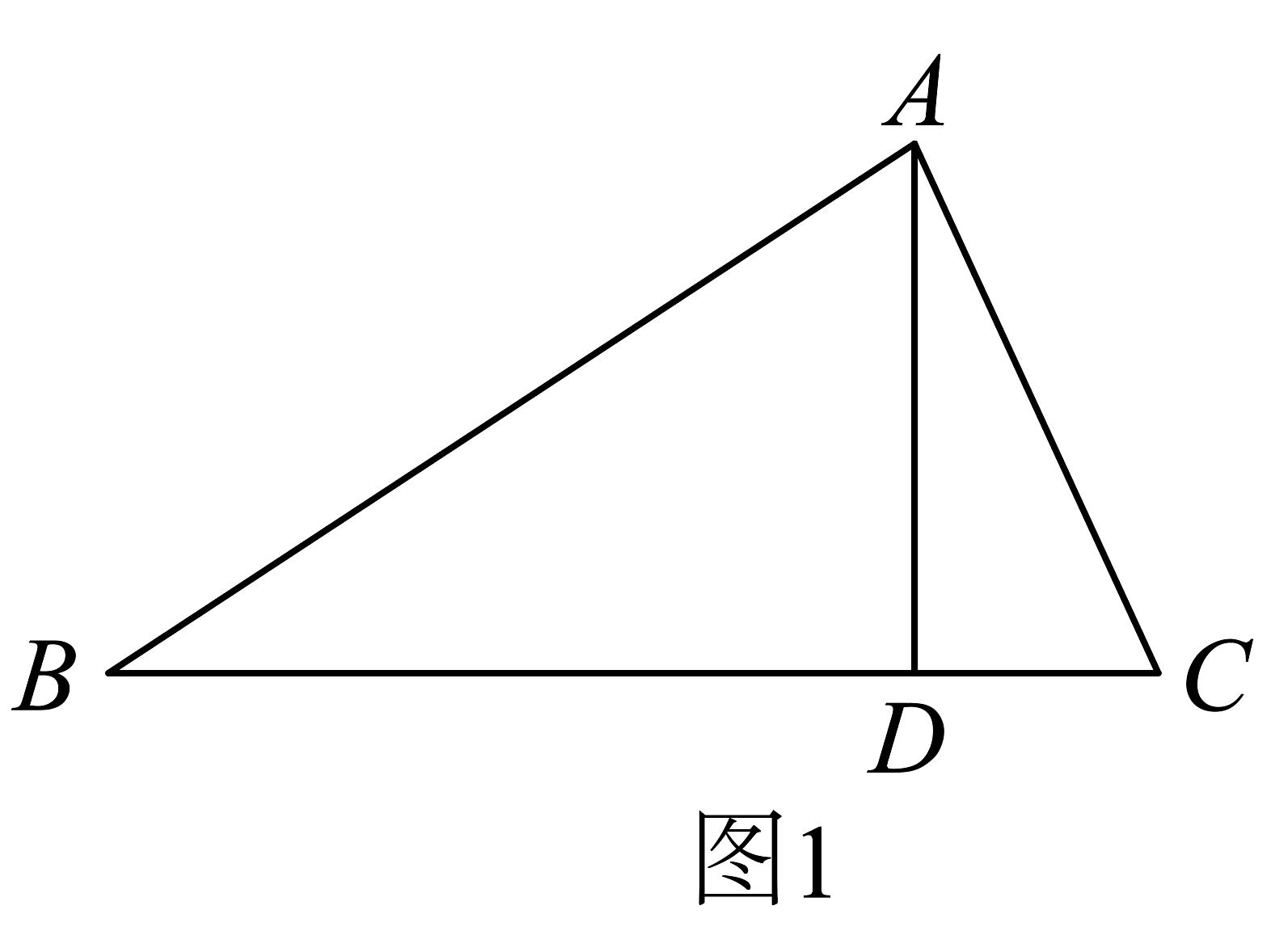
小明同学的思路是:将沿折叠,点刚好落在边上的点处.请你根据小明的思路直接写出_________.
【探究】如图2, , 为的外角的平分线,交的延长线于点 , 则线段、、又有怎样的数量关系?请写出你的猜想并证明.
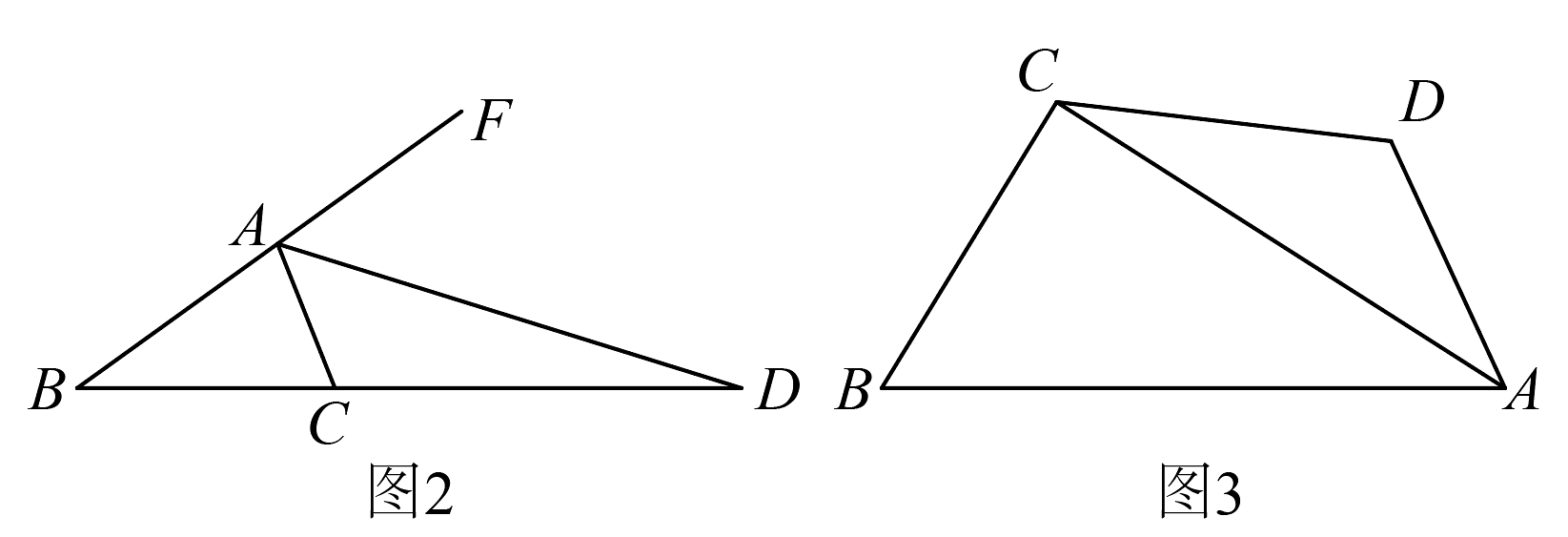
【拓展】如图3,在四边形中,平分 , , .
①求证:;
②若 , 则的长为_____________.
-
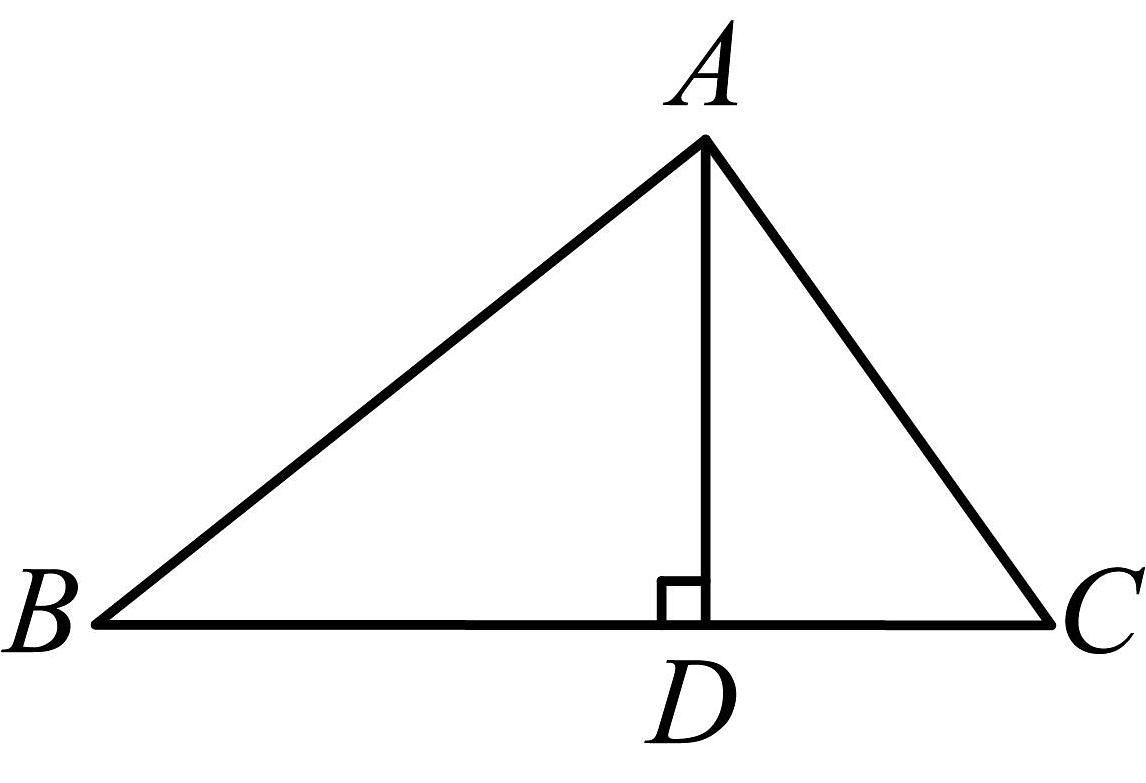
9、在学校组织的研学活动中,需要学生自己搭建帐篷.下图是搭建帐篷的示意图.在中,支架从帐篷顶点支撑在水平的支架上,且于点 , 经测量得: , , . 按照要求,帐篷支架与所夹的角需为直角.请通过计算说明学生搭建的帐篷是否符合条件.
-
10、阅读下面的内容.
比较与的大小
“嘉嘉”的思路:
将 , 两个式子分别平方后,再进行比较.
“淇淇”的思路:
以、 , 为三边构造一个 , 再利用三角形的三边关系进行比较.
请利用嘉嘉、淇淇的思路分别进行说明.
-
11、已知一个底面为正方形的长方体,高是底面边长的2倍,体积为 . 求:(1)、这个长方体的底面边长;(2)、这个长方体的表面积.
-
12、如图,在中, , 是边的垂直平分线,连接 .
 (1)、若 , 求的长;(2)、若平分 , 求的度数.
(1)、若 , 求的长;(2)、若平分 , 求的度数. -
13、已知 , 且 , , , 点、分别在、上滑动.
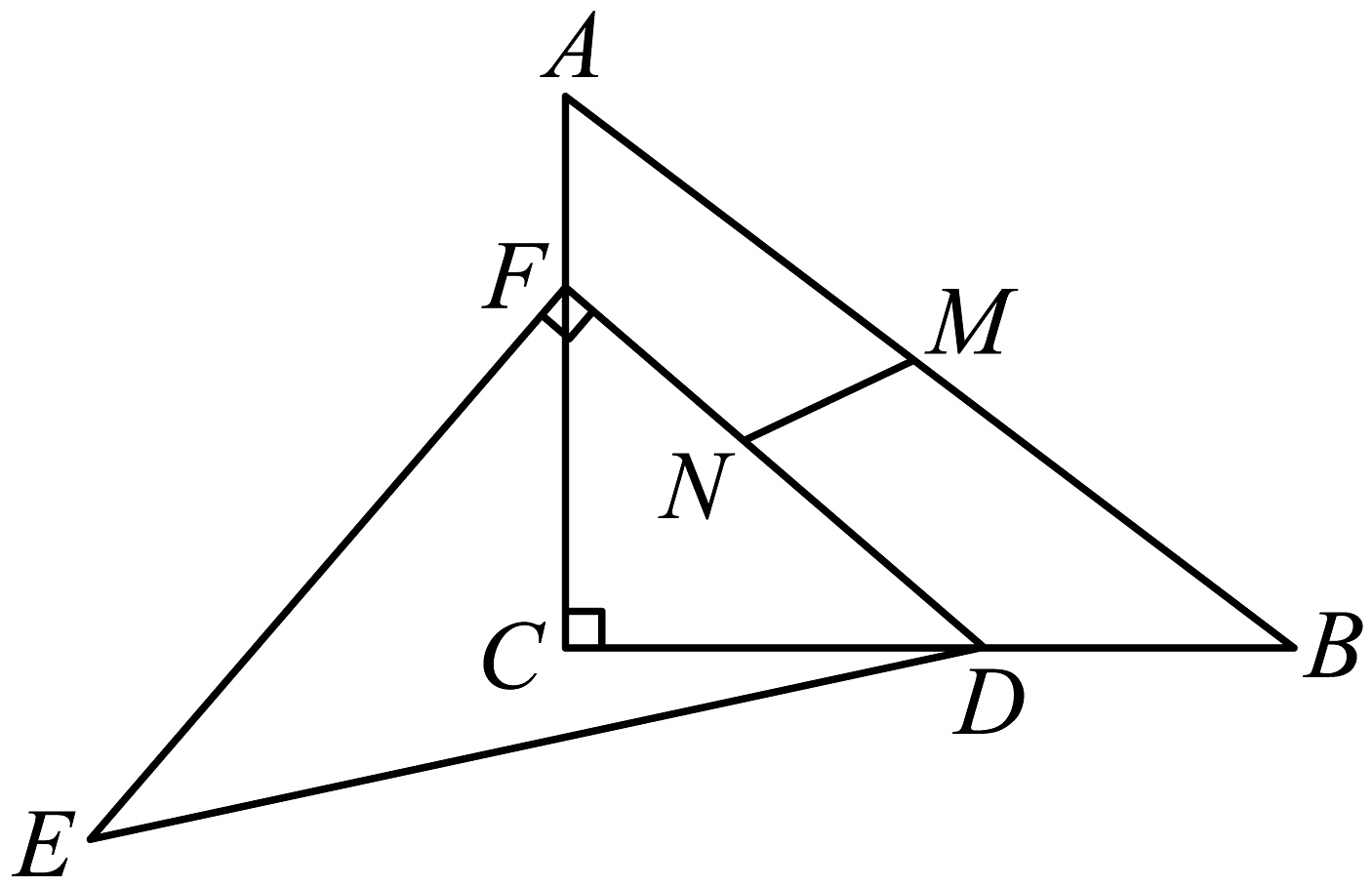
(1);
(2)点是的中点,点是的中点,则的最小值是 .
-
14、如图, , 点A在上,且 , 按下列要求画图:
以A为圆心,1为半径向右画弧,交于点A1 , 得到第1条线段 .
以为圆心,1为半径向右画弧,交于点 , 得到第2条线段 .
以为圆心,1为半径向右画弧,交于点 , 得到第3条线段 .
……这样画下去,直到第条线段,之后就不能再画出符合要求的线段了,则( )
 A、15 B、14 C、13 D、12
A、15 B、14 C、13 D、12 -
15、如图,、E是直线上不重合的两点,是的角平分线,于点A,若的周长为10,则的周长可能是( )
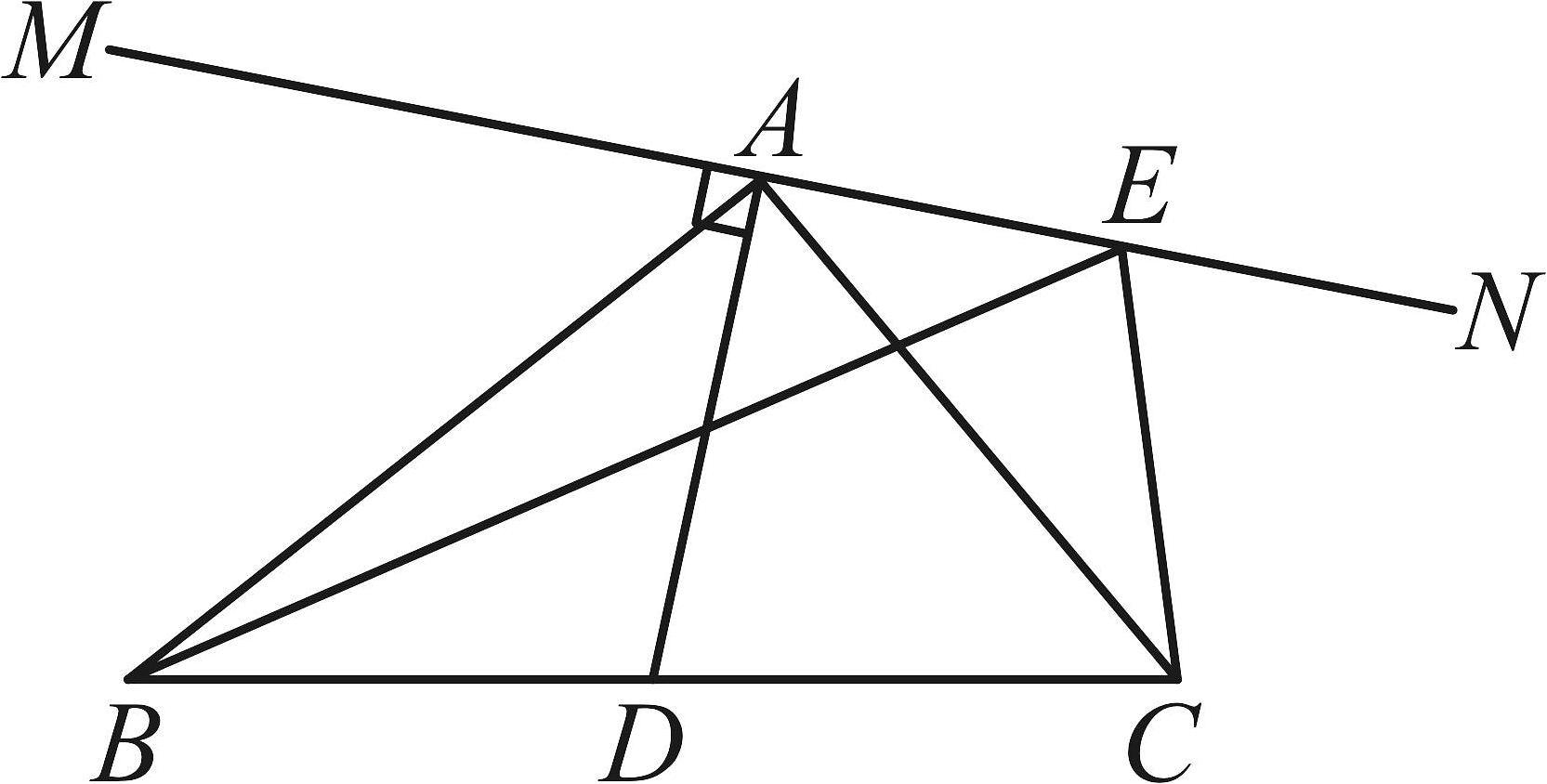 A、8 B、9 C、10 D、11
A、8 B、9 C、10 D、11 -
16、小明在纸上书写了一个正确的演算过程,同桌小亮一不小心撕坏了一角,如图所示,则撕坏的一角中“”为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
17、如图,根据尺规作图痕迹,图中标注在点A处所表示的数为( )
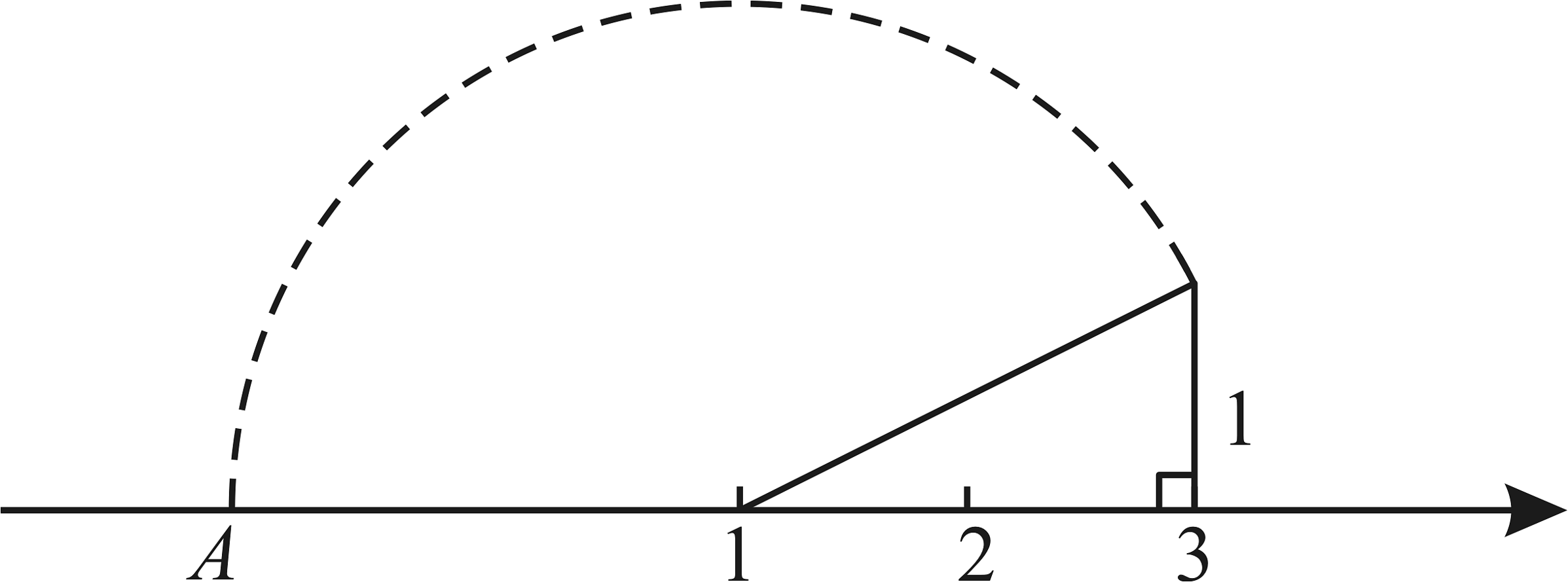 A、 B、 C、 D、
A、 B、 C、 D、 -
18、某班开展“用直尺和圆规作角平分线”的探究活动,甲、乙两个同学展示作图痕迹如下,其中射线为平分线的是( )
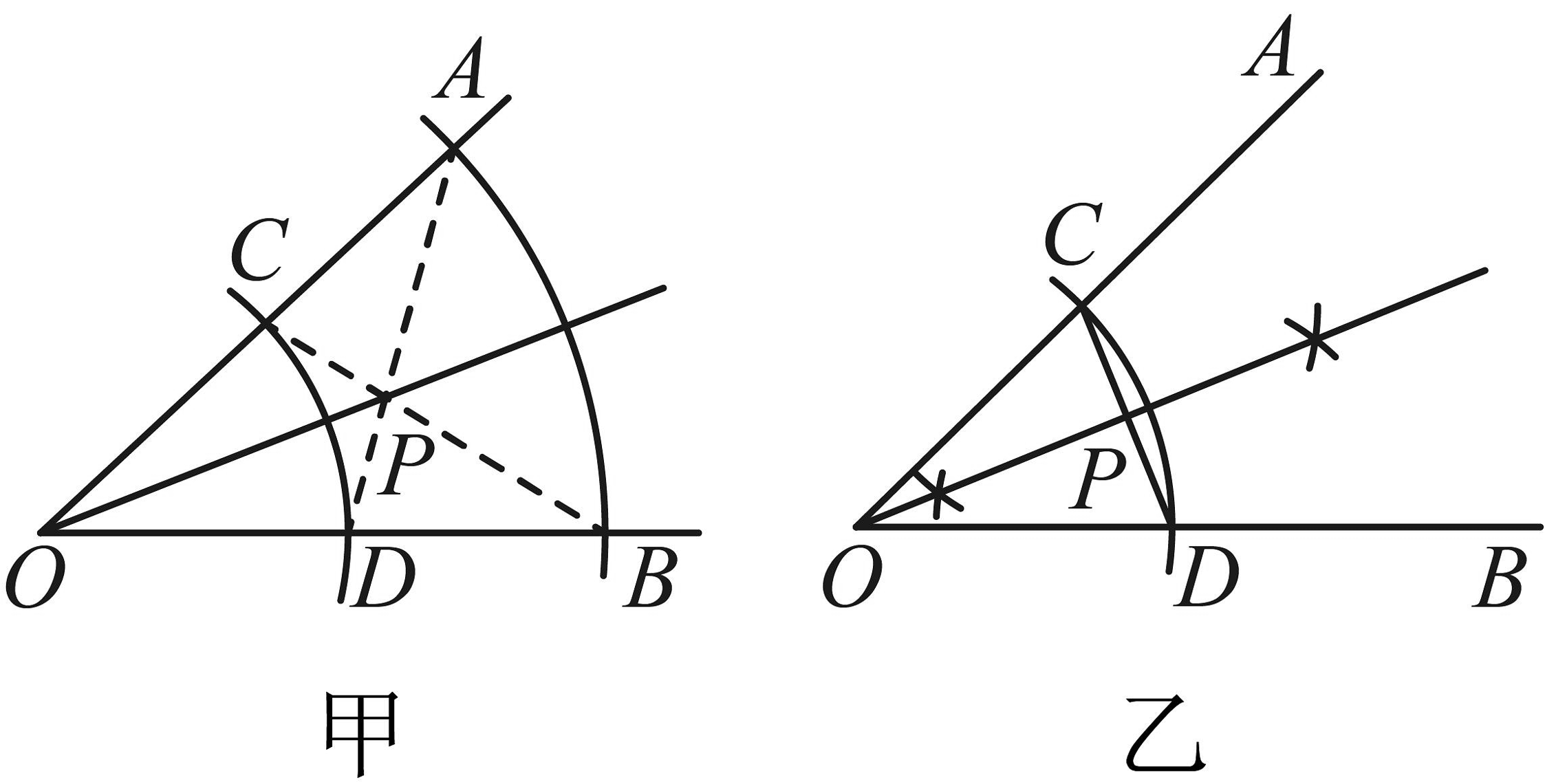 A、甲 B、乙 C、甲和乙 D、甲、乙均不是
A、甲 B、乙 C、甲和乙 D、甲、乙均不是 -
19、的平方根是( )A、2 B、4 C、 D、
-
20、如图,点E是边BC上的一点不与点B、C重合 , , .
 (1)、图1,若 , , 则的度数为;(2)、图2,若 , 求的度数;用含的代数式表示(3)、图3,已知且 , , 且 , 点E在线段上运动时,连接 , M为的中点,探究的长度是否存在最小值?若存在,用关于m,n的代数式表示出来;若不存在,请说明理由.
(1)、图1,若 , , 则的度数为;(2)、图2,若 , 求的度数;用含的代数式表示(3)、图3,已知且 , , 且 , 点E在线段上运动时,连接 , M为的中点,探究的长度是否存在最小值?若存在,用关于m,n的代数式表示出来;若不存在,请说明理由.