第十三章《三角形中的边角关系、命题与证明》提升卷—沪科版数学八(上)单元分层测
试卷更新日期:2025-09-21 类型:单元试卷
一、选择题:本大题共12小题,每小题3分,在每小题给出的四个选项中,只有一个是正确的.每小题选对得3分,选错、不选或多选,均不得分.
-
1. 下列语句是命题的是( )A、把绕着点A旋转 B、三角形三个角的平分线的交点是这个三角形的重心吗? C、作的边上的高 D、三角形一个外角大于这个三角形的任何一个内角2. 对于一次函数 , 下列命题是假命题的是( )A、函数值随自变量的增大而减小 B、图象不经过第三象限 C、向左平移2个单位后经过原点 D、图象与y轴交于点3. 下列命题的逆命题是真命题的是( )A、如果 , 那么 B、如果两个角都是直角,那么这两个角相等 C、对顶角相等 D、相等的角是内错角4. 能说明命题“若x为无理数,则x2也是无理数”是假命题的反例是( )A、 B、 C、 D、5. 对于命题“如果 , 那么”,能说明该命题为假命题的反例是( )A、 , B、 , C、 , D、 ,6. 某班有20名同学参加围棋、象棋比赛.甲说:只参加一项的人数大于14人;乙说:两项都参加的人数小于5人.对于甲、乙两人的说法,有下列命题,其中是真命题的是( ).A、若甲对,则乙对 B、若乙对,则甲对 C、若乙错,则甲错 D、若甲错,则乙对7. 如图所示,在△ABC中,∠B=67°,∠C=33°,AD是△ABC的角平分线,则∠CAD的度数为( )
 A、40° B、45° C、50° D、55°8. 如图,下面的四个盒子中,每个盒子里都有两根小棒,把其中的一根小棒用剪刀按图中所示的位置剪成两段,这两段小棒再与另一根小棒首尾相接,能够围成一个三角形的是( )A、
A、40° B、45° C、50° D、55°8. 如图,下面的四个盒子中,每个盒子里都有两根小棒,把其中的一根小棒用剪刀按图中所示的位置剪成两段,这两段小棒再与另一根小棒首尾相接,能够围成一个三角形的是( )A、 B、
B、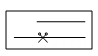 C、
C、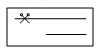 D、
D、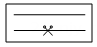 9. 等腰三角形的底边长与其腰长的比值称为这个等腰三角形的“优美比”.若等腰的周长为20,其中一边长为8,则它的“优美比”为( )A、 B、 C、或2 D、或10. 如图,在同一平面内将15cm长的细铁丝AB弯折成一个三角形.
9. 等腰三角形的底边长与其腰长的比值称为这个等腰三角形的“优美比”.若等腰的周长为20,其中一边长为8,则它的“优美比”为( )A、 B、 C、或2 D、或10. 如图,在同一平面内将15cm长的细铁丝AB弯折成一个三角形.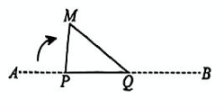
(1)量出AP = 4cm:(2)在点P右侧取一点Q,使PQ>4cm;(3)将AP向右翻折,BQ向左翻折.若要使A,B两点能在点M处重合,则PQ长可能为( )A、7cm B、8cm C、9cm D、10cm11. 在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m,其行走路线如图所示,第1次移动到A1 , 第2次移动到A2……第n次移动到 An,则△OA2A2018的面积是( ). A、 B、 C、 D、12. 如图, , 、、分别平分、、 . 以下结论,其中正确的是( )
A、 B、 C、 D、12. 如图, , 、、分别平分、、 . 以下结论,其中正确的是( )①;②;③;④ .
 A、①② B、②③④ C、①③④ D、①②③④
A、①② B、②③④ C、①③④ D、①②③④二、填空题:本大题共4小题,每小题4分,共16分.只要求填出最后结果.
-
13. 把命题“互为相反数的两个数的和为零”写成“如果…那么…”的形式:.14. 下列命题中逆命题成立的有 . (填序号).
①同旁内角互补,两直线平行; ②如果两个角是直角,那么它们相等;
③如果 , 那么 , ; ④如果两个实数相等,那么它们的平方相等.
15. 如图,点G为△ABC的重心,D,E,F分别为BC,AB的中点,具有性质:AG:GD=BG:GE=CG:GF=2:1.已知△AFG的面积为3 . 16. 如图,在中, , , D为边BC延长线上一点,BF平分 , E为射线BF上一点.若直线CE垂直于的一边,则的度数为 .
16. 如图,在中, , , D为边BC延长线上一点,BF平分 , E为射线BF上一点.若直线CE垂直于的一边,则的度数为 .
三、解答题:本大题共8小题,共68分
-
17. 如图是的小正方形构成的网格,每个小正方形的边长为1,的三个顶点 , , 均在格点上,请仅用无刻度的直尺,在给定的网格中按要求画图,保留作图痕迹.
图1
 图2
图2 (1)、三角形的面积为;(2)、在图1中画出边上高;(3)、在图2中作出的角平分线 .18. 《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某兴趣小组统计阅读过这四大名著的人数,同时满足以下三个条件:
(1)、三角形的面积为;(2)、在图1中画出边上高;(3)、在图2中作出的角平分线 .18. 《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某兴趣小组统计阅读过这四大名著的人数,同时满足以下三个条件:①阅读过《西游记》的人数多于阅读过《水浒传》的人数;
②阅读过《水浒传》的人数多于阅读过《三国演义》的人数;
③阅读过《三国演义》的人数的2倍多于阅读过《西游记》的人数.
若阅读过《三国演义》的人数为4,设阅读过《西游记》的人数是a,阅读过《水浒传》的人数是b(a,b均为整数).
(1)、根据题意列出不等式.(2)、请根据以上推理,求出阅读过《水浒传》的人数.19. 如图,在中, , 三个内角的平分线交于点O.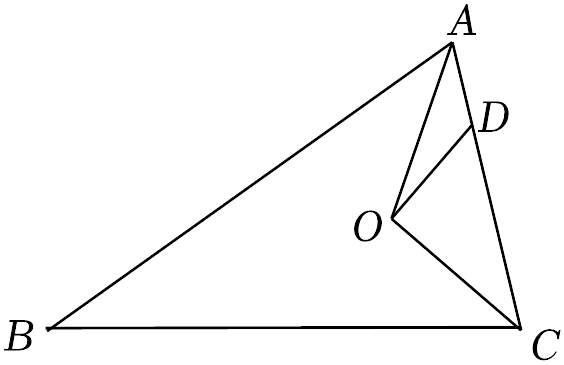 (1)、若 , 求的度数;(2)、过点O作 , 交于点D.试说明: .20. 如图,△ABC的三条角平分线相交于点I,过I作DE⊥AI,分别交AB,AC于点D,E.
(1)、若 , 求的度数;(2)、过点O作 , 交于点D.试说明: .20. 如图,△ABC的三条角平分线相交于点I,过I作DE⊥AI,分别交AB,AC于点D,E. (1)、请你通过画图、度量,填写下表(图画在草稿纸上,并尽量画准确)
(1)、请你通过画图、度量,填写下表(图画在草稿纸上,并尽量画准确)∠BAC的度数
30°
64°
80°
120°
∠BIC的度数
∠BDI的度数
(2)、根据表格中的数据,猜想∠BIC与∠BDI之间的数量关系,并说明理由.21. 如图,直线的解析表达式为: , 且与轴交于点 , 直线经过点 , , 直线 , 交于点 . (1)、点的坐标;(2)、求直线的表达式;(3)、求的面积;(4)、在直线上存在异于点的另一点 , 使得的面积是面积的2倍,求点的坐标.22. 如图①,兔子在第一次龟兔赛跑失利后,不服输的它又组织了一次比赛,这次的比赛规则是从点A 跑到点 B,但A,B之间设置了很多陷阱,兔子选择沿路线A→C→B 前进,乌龟可以选择的路线分别是:路线①A→C→B;路线②A→E→F→B;路线③A→D→B.
(1)、点的坐标;(2)、求直线的表达式;(3)、求的面积;(4)、在直线上存在异于点的另一点 , 使得的面积是面积的2倍,求点的坐标.22. 如图①,兔子在第一次龟兔赛跑失利后,不服输的它又组织了一次比赛,这次的比赛规则是从点A 跑到点 B,但A,B之间设置了很多陷阱,兔子选择沿路线A→C→B 前进,乌龟可以选择的路线分别是:路线①A→C→B;路线②A→E→F→B;路线③A→D→B. (1)、若乌龟选择了路线③,那么乌龟和兔子的路线哪个更短呢?请说明理由.
(1)、若乌龟选择了路线③,那么乌龟和兔子的路线哪个更短呢?请说明理由.以下是小明不完整分析过程,请你帮他补充完整;
解:乌龟的路线更短,理由如下:
如图②,延长AD交 BC 于点 P,
在 中,AC+CP>AP,
…
(2)、请你帮乌龟从路线②和③中选择一条较短的路线,并说明理由.23. 如图,点E在平行线AB,CD之间,且在线段AC的左侧. (1)、求证:∠BAE+∠ECD+∠AEC=360°.(2)、若点E向右移动到线段AC的右侧,此时∠BAE,∠AEC,∠ECD之间的关系仍然满足(1)中的结论吗?若满足,给出证明;若不满足,请你写出正确的结论并证明.(要求:画出相应的图形)(3)、继续移动点E的位置,还能得到哪些新论断?写出你的论断.24. 综合与探究:
(1)、求证:∠BAE+∠ECD+∠AEC=360°.(2)、若点E向右移动到线段AC的右侧,此时∠BAE,∠AEC,∠ECD之间的关系仍然满足(1)中的结论吗?若满足,给出证明;若不满足,请你写出正确的结论并证明.(要求:画出相应的图形)(3)、继续移动点E的位置,还能得到哪些新论断?写出你的论断.24. 综合与探究: (1)、【情境引入】
(1)、【情境引入】
如图1,BD,CD分别是OABC的内角∠ABC,∠ACB的平分线,证明:∠D=90°+∠A.(2)、【深入探究】
①如图2,BD,CD分别是△ABC的两个外角∠EBC,∠FCB的平分线,∠D与∠A之间的等量关系是 ▲ .②如图3,BD,CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线,BD,CD交于点D,探究∠D与∠A之间的等量关系,并说明理由.