第十四章《全等三角形》基础卷—沪科版数学八（上）单元分层测
试卷更新日期：2025-09-21 类型：单元试卷
一、选择题：本大题共12小题，每小题3分，在每小题给出的四个选项中，只有一个是正确的.每小题选对得3分，选错、不选或多选，均不得分.
-
1. 下列各组的两个图形属于全等图形的是（ ）A、
B、
C、
D、
2. 下列说法正确的是（ ）A、形状相同的两个图形一定全等 B、两个三角形是全等图形 C、两个全等图形面积一定相等 D、两个正方形一定是全等图形3. 如图是两个全等三角形，字母a，b，c分别表示三角形的边长，根据图中数据，则∠1 的度数为( )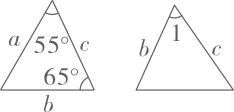
A、55° B、60° C、65° D、66°4. 如图， ， ， ， 三点在一条直线上，下面结论不一定正确的是（ ）
A、 B、 C、 D、5. 如图， ， 边和在同一条直线上．若 ， ， 则长为（ ）．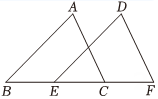
A、 B、 C、 D、6. 如图， △ABC≌△DEF，若∠B=125°， ∠F=35°，则∠A的度数为（ ）
A、35° B、30 C、25° D、20°7. 如图，数学辅导书上的三角形被墨水污染了，根据所学知识可以在空白纸上画出一个完全一样的三角形，其依据是 ( )
A、SSS B、ASA C、AAS D、SAS8. 如图，AE=AC，∠1=∠2，若要用“ASA”证明△ABC≌△ADE，则还需要添加的条件是（ )
A、∠B=∠D B、∠1=∠D C、∠E=∠C D、∠2=∠C9. 如图是嘉嘉为参加手工比赛制作燕子风筝的骨架图，已知AC=AD，AB=AE，∠BAD=∠EAC，∠D=35°，则∠C的度数为 ( )
A、30° B、35° C、40° D、45°10. 竹骨伞是传统手工艺品，如图是一把竹骨伞完全撑开时的平面示意图，伞骨DE=DF，伞面上的点E，F到伞顶A 的距离相等.若伞面与伞柄所成角∠BAD 的度数为55°，则∠BAC 的度数为 （ ）
A、105° B、110° C、115° D、120°11. 如图，在△ABC中，∠ABC=90°，DE⊥AB 于点 E，交AC 于点 F，且DE=AB=4，连接BD，若BD=AC，BC=2，则AE的长为 ( )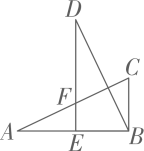
A、2 B、3 C、4 D、512. 小丽与爸妈在公园里荡秋千．如图，小丽坐在秋千的起始位置A处，OA与地面垂直，两脚在地面上用力一蹬，妈妈在距地面1m高的B处接住她后用力一推，爸爸在C处接住她．若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和1.8m，∠BOC＝90°．爸爸在C处接住小丽时，小丽距离地面的高度是（ ）．
A、1m B、1.6m C、1.8m D、1.4m二、填空题：本大题共4小题，每小题4分，共16分.只要求填出最后结果.
-
13. 下列图形中， 图①与图⑧是全等图形．再找出两对全等图形：.
14. 如图是一种常见的户外健身器材，其支架的三角结构运用的数学原理是
15. 如图，△ADE≌△BCF，AD=8 cm，CD=6 cm，则BD的长为cm.
16. 如图，已知 欲说明 ， 则可以补充的条件是.(写出一个即可)
三、解答题：本大题共7小题，共68分.
-
17. 如图，在方格纸中，的三个顶点及A、B、C、D、E五个点都在小方格的顶点上．现以A、B、C、D、E中的三个点为顶点画三角形．
(1)、在图甲中画出一个三角形与全等；(2)、在图乙中画出一个三角形与面积相等但不全等 ．18. 命题：全等三角形的对应边上的高相等.(1)、先把这个命题写成“如果……，那么……”的形式，再写出这个命题的逆命题.(2)、判断原命题的真假，如果是假命题，请举出一个反例；如果是真命题，请写出证明过程.19. 如图，已知△ABC 中，AB=AC，D 为AB 上一点，E为AC 延长线上一点，BD=CE，DE 交BC于点F.求证：DF=EF.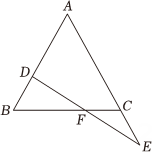
20. 如图，某段河流的两岸是平行的，某校八年级数学兴趣小组在林老师带领下不用涉水过河就测得河的宽度，他们是这样做的：①在树A的对岸正对位置选一点B，使得；
②从点B沿河岸直走25米有一树C，继续前行25米到达D处；
③从D处沿河岸垂直的方向行走到达E处，使得树A、树C、点E三点共线；
④测得的长为20米．
(1)、根据他们的做法补全图形并标出点B、D、E的位置；(2)、求该段河流的宽度是多少米？21. 明明在错题集中整理了这样一道题：如图①，D 为△ABC 内一点，连接AD，BD，CD，AD 平分∠BAC，BD=CD，若∠ABD=∠ACD，求证：∠1=∠2.证明：如图②，延长AD交BC 于点 E，
在△ABD和△ACD中.
∴△ABD≌△ACD(SSA)， 第一步
∴∠ADB=∠ADC，
∴∠BDE=∠CDE，
在△BDE 和△CDE中，
∴△BDE≌△CDE(SAS)， 第二步
∴∠1=∠2. 第三步
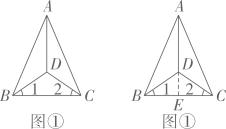(1)、请帮明明分析他出错的地方在第步，出错的原因是；(2)、请帮他写出正确的解题过程.22. 【问题情境】数学活动课上，老师组织同学们以“全等三角形线段间的数量关系”为主题开展数学活动.
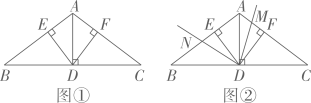(1)、【初步探索】如图①，在 中， 于点 D， 于点 E， 于点 F，则线段 DE 与 DF 的数量关系为；(2)、【拓展延伸】如图②，若M 是线段AF 上一点，作 ， 射线 DN交AB 于点 N，写出线段AM，EN，AE 之间的数量关系，并说明理由.23. [阅读理解]课外兴趣小组活动时，老师提出了如下问题：如图1，在中，若 ， 求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：如图2，延长AD到点E ， 使 ， 连结BE ， 请根据小明的方法思考：
图1
图2 
图3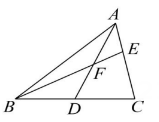
(1)、由已知和作图能得到 ， 其理由是什么？(2)、求AD的取值范围．(3)、如图3，AD是的中线，BE交AC于点F ， 且 ， 试说明 ．