第十三章《三角形中的边角关系、命题与证明》基础卷—沪科版数学八（上）单元分层测

试卷更新日期：2025-09-21 类型：单元试卷

进入出卷网下载

一、选择题：本大题共12小题，每小题3分，在每小题给出的四个选项中，只有一个是正确的.每小题选对得3分，选错、不选或多选，均不得分.

1. 如图所示，小手盖住了一个三角形的一部分，则这个三角形是（）

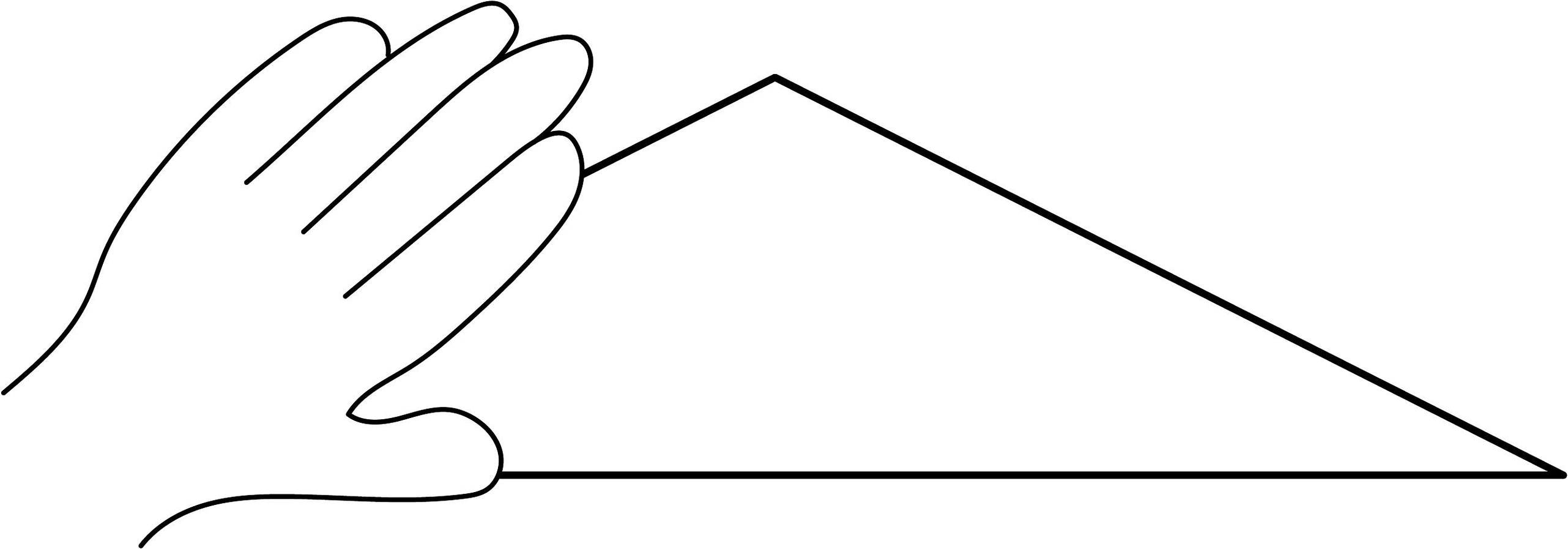A、直角三角形 B、锐角三角形 C、钝角三角形 D、等边三角形

查看试题解析
2. 观察下列图形，是三角形的是（）

A、 B、 C、 D、

查看试题解析
3. 木工师傅要做一个三角形木架，有两根木条的长度为7cm和14cm，第三根木条的长度可以是（）

A、5cm B、18cm C、21cm D、23cm

查看试题解析
4. 如图，把含有60°的直角三角板斜边放在直线l上，则∠α的度数是（）

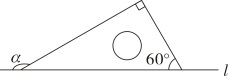A、120 B、130° C、140° D、150°

查看试题解析
5. 如图，在 $△ A B C$ 中，已知点D，E分别为 $B C ， A D$ 的中点，若 $S_{△ A E C} = 1$ ，则 $S_{△ A B C} =$ （）

A、2 B、3 C、4 D、6

查看试题解析
6. 下列各图中，作△ABC边AB上的高，正确的是 ( )

A、 B、 C、 D、

查看试题解析
7. 下列语句中，是定义的是（）

A、两点确定一条直线 B、在同一平面内，不相交的两条直线叫作平行线 C、对顶角相等 D、同角的余角相等

查看试题解析
8. 下列语句中，不是命题的是（）

A、两点之间线段最短 B、内错角都相等 C、连接A ， B两点 D、平行于同一直线的两直线平行

查看试题解析
9. 在证明命题“若 “>1，则 a>1”是假命题时，下列选项中所举反例正确的是（）

A、a=-2 B、a=2 C、a=3 D、a=4

查看试题解析
10. 下列命题中，是真命题的是（）

A、同旁内角互补 B、两直线被第三条直线所截，截得的内错角相等 C、三角形的外角大于三角形的内角 D、对顶角相等

查看试题解析
11. 如图，在 $△ A B C$ 中，外角 $∠ A C D = 100^{\circ}, ∠ B = 40^{\circ}$ ，则 $∠ A$ 的度数为（）

A、 $40^{\circ}$ B、 $50^{\circ}$ C、 $60^{\circ}$ D、 $100^{\circ}$

查看试题解析
12. A，B，C，D，E五名学生猜测自己能否进入市中国象棋前三强．A说：“如果我进入，那么B也进入．”B说：“如果我进入，那么C也进入．”C说：“如果我进入，那么D也进入．”D说：“如果我进入，那么E也进入，”大家都没有说错，则进入前三强的三个人是（）

A、A，B，C B、B，C，D C、D，E，A D、C，D，E

查看试题解析

二、填空题：本大题共4小题，每小题4分，共16分.只要求填出最后结果.

13. 请将命题“平行于同一直线的两直线互相平行”改成“如果，那么”的形式：．

查看试题解析
14. 定理“等角的补角相等”的逆命题是．

查看试题解析
15. 如图，∠ACD是△ABC的外角，若∠ACD＝110°，∠A＝80°，则∠B＝°.

查看试题解析
16. 如图，已知 $C D$ 和 $B E$ 是 $△ A B C$ 的角平分线， $∠ A = 60 °$ ，则 $∠ B O C =$ ．

查看试题解析

三、解答题：本大题共7小题，共68分.

17. 在平面直角坐标系中，作出 $△ A B C$ ，使各顶点的坐标分别是： $A (1, 2)$ ， $B (- 2, - 2)$ ， $C (3, - 2)$ ，并求出 $△ A B C$ 的面积．

查看试题解析
18. 如图，已知点A， B在直线a上，点C， D， E在直线b上.以点A，B，C，D，E中的任意三点作为三角形的顶点，一共可以组成多少个三角形?分别写出这些三角形

查看试题解析
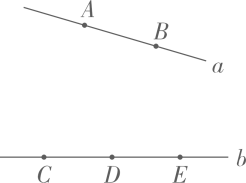19. 如图，在△ABC 中， AD 是高， AE， BF 是角平分线，且AE， BF 相交于点O，∠BAC=50°， ∠C=70°. 求∠DAC 和∠BOA 的度数.

查看试题解析
20. 如图， CE 是△ABC 的外角∠ACD 的平分线，且 CE 交 BA 的延长线于点E. 求证∠BAC=∠B+2∠E.

查看试题解析
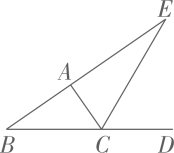21. 在△ABC中，∠A＝ $\frac{1}{2}$ ∠B＝ $\frac{1}{3}$ ∠ACB，CD是△ABC的高，CE是∠ACB的角平分线，求∠DCE的度数．

查看试题解析
22. 【定义】若一个三角形三边长均为偶数，则称这个三角形为“好运三角形” $．$ 例如，三边为 $6$ ， $8$ ， $10$ 的三角形是“好运三角形”．

(1)、【概念运用】在 $△ A B C$ 中， $A B = 2$ ， $B C = 4$ ，若 $△ A B C$ 为“好运三角形”，求 $A C$ 的长；

(2)、【变式运用】已知 $△ A B C$ 的周长为 $16$ ， $A C = 4$ ，若 $A B$ 的长为偶数，试判断 $△ A B C$ 是否为“好运三角形”．

查看试题解析
23. 阅读材料：
在一个三角形中，如果一个内角 $α$ 的度数是另一个内角度数的3倍，那么这样的三角形我们称为“优雅三角形”，其中 $α$ 称为“优雅角”．例如：一个三角形三个内角的度数分别是 $30 °, 90 °, 60 °$ ，这个三角形就是“优雅三角形”，其中“优雅角”的度数为 $90 °$ ；反之，若一个三角形是“优雅三角形”，则这个三角形的三个内角中一定有一个内角 $α$ 的度数是另一个内角度数的3倍．

(1)、一个“优雅三角形”的一个内角为 $120 °$ ，若“优雅角”为锐角，则这个“优雅角”的度数为；

(2)、如图， $∠ M O N = 60 °$ ，在射线 $O M$ 上取一点A，过点A作 $A B ⊥ O M$ ，交 $O N$ 于点B，以A为端点画射线 $A C$ ，交线段 $O B$ 于点C（点C不与点O，B重合），得到一个以 $∠ A O C$ 为“优雅角”的“优雅角三角形” $A O C$ ，求 $∠ A C B$ 的度数．

查看试题解析