-
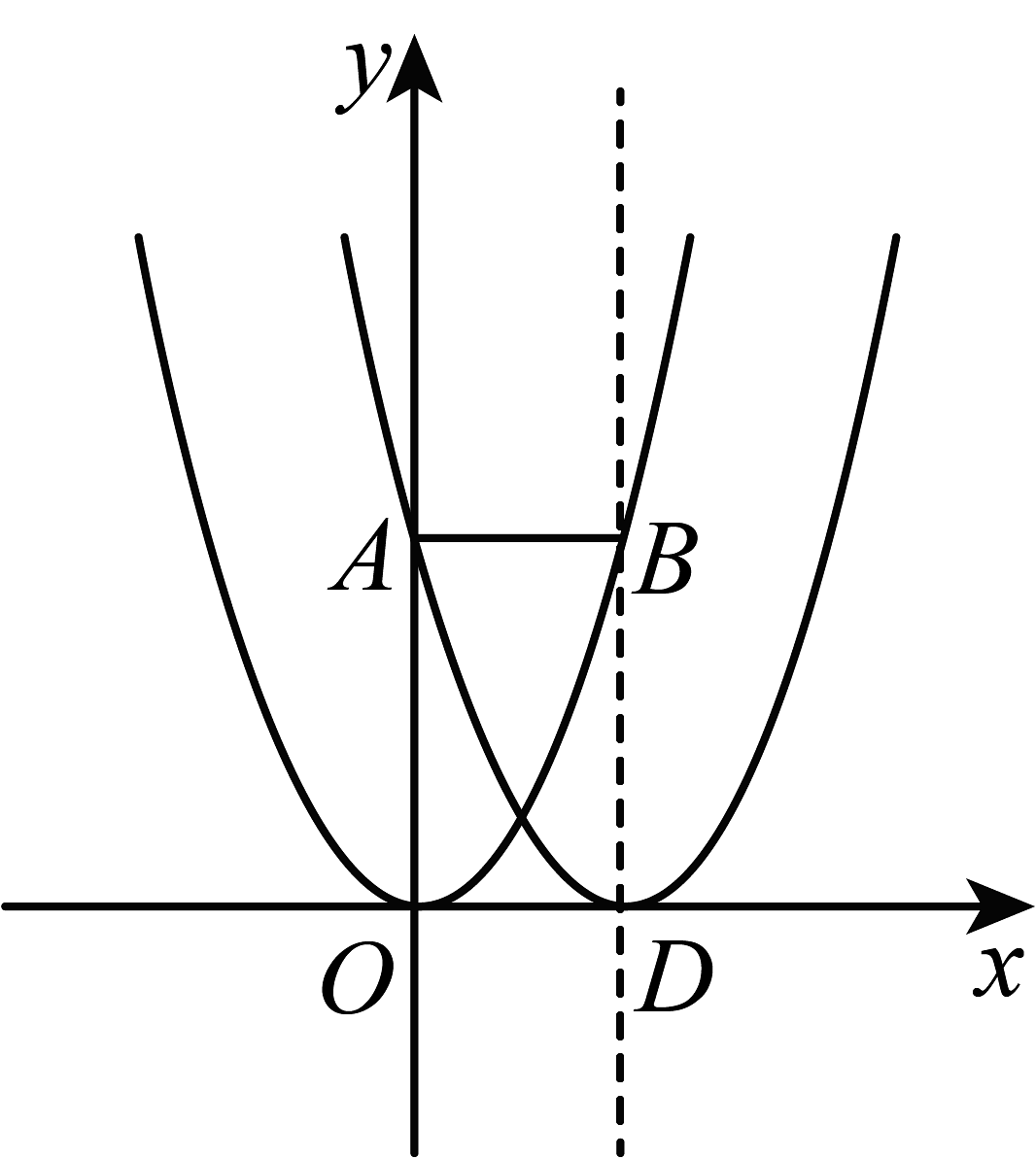
1、如图,将二次函数的图象向右平移2个单位长度,所得新拋物线的顶点为D,并与y轴交于点A,对称轴与函数的图象的交点为 , 若新抛物线存在点P使以D为底的等腰三角形,则点P的坐标为 .
-
2、某地进行“迎国庆振兴杯”篮球邀请赛,赛制为单循环(每两队之间赛一场),若计划安排21场比赛,则邀请个球队参赛.
-
3、已知点与点关于原点对称,则点的坐标为 .
-
4、小明用公式法解方程 , 请帮他填空第一步,解: , , .
-
5、拋物线的对称轴是轴.
-
6、如图是抛物线图象的一部分,抛物线的顶点是点 , 对称轴是直线 , 且抛物线与轴的一个交点为;直线的解析式为 , 下列结论:①;②;③方程有一个实数根;④抛物线与轴的另一个交点是;⑤当时,则 , 其中正确的是( )
 A、①②③ B、③⑤ C、①④ D、④⑤
A、①②③ B、③⑤ C、①④ D、④⑤ -
7、已知二次函数的图象如图所示,关于该函数在所给自变量取值范围内,下列说法正确的是( )
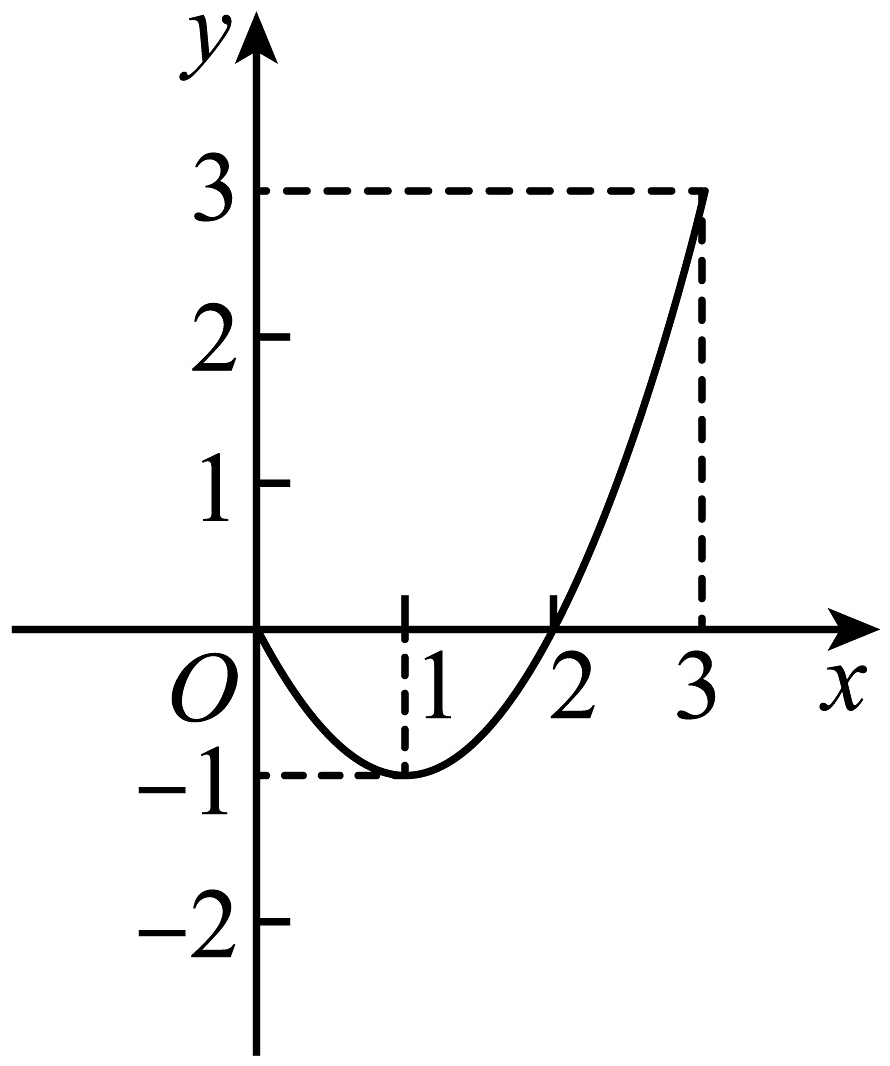 A、有最小值0,有最大值2 B、有最小值0,有最大值3 C、有最小值 , 有最大值2 D、有最小值 , 有最大值3
A、有最小值0,有最大值2 B、有最小值0,有最大值3 C、有最小值 , 有最大值2 D、有最小值 , 有最大值3 -
8、若二次函数的图象与轴有两个交点,则关于的一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定
-
9、把抛物线向左平移1个单位,再向上平移3个单位,则平移后抛物线的解析式为( )A、 B、 C、 D、
-
10、如图,中, , 在同一平面内,将绕点A逆时针旋转到位置,则等于( )
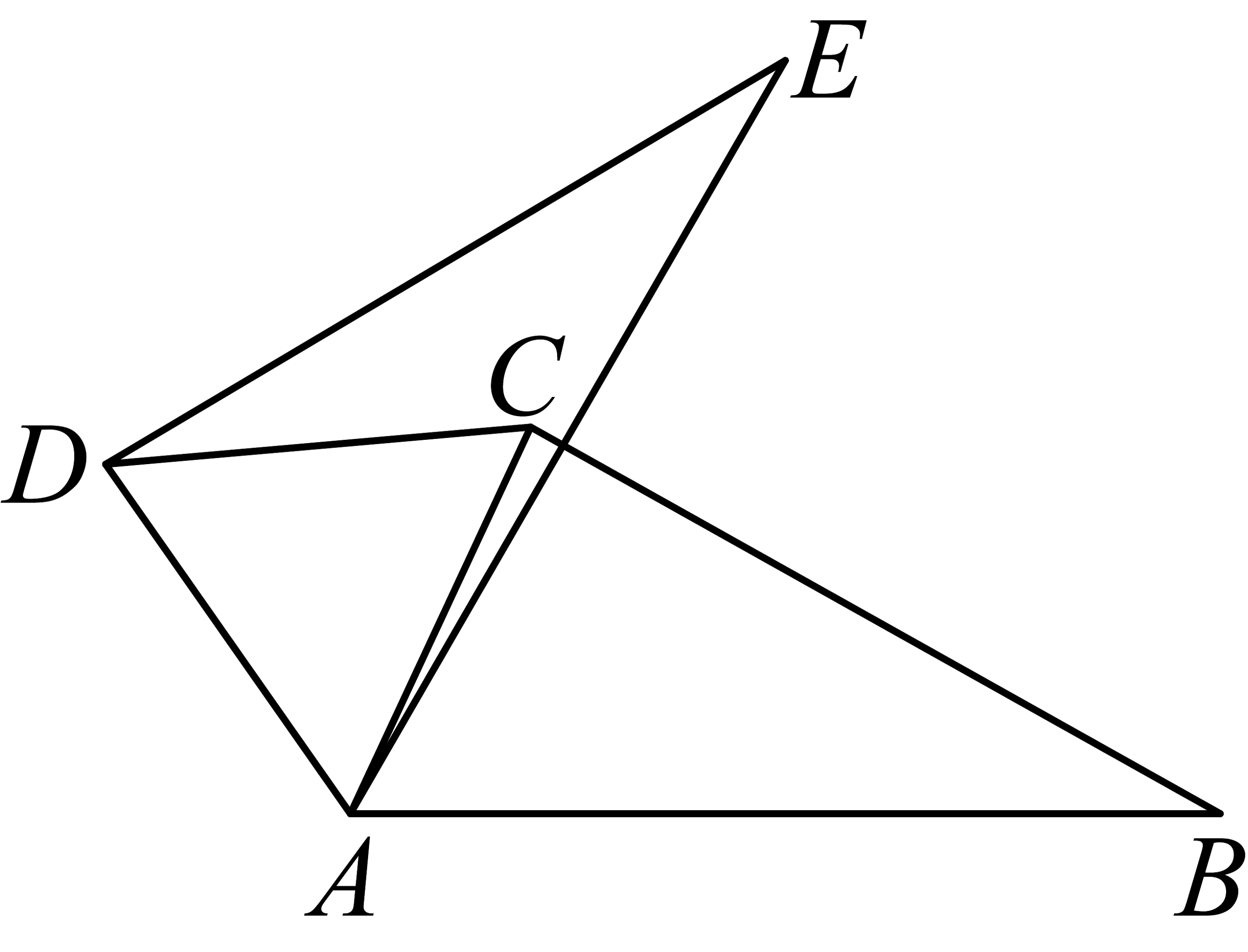 A、 B、 C、 D、
A、 B、 C、 D、 -
11、用配方法解方程 , 原方程应变形为( )A、 B、 C、 D、
-
12、二次函数的顶点坐标是( )A、 B、 C、 D、
-
13、如图下面的图形绕直线l旋转一周后得到的立体图形是( )
 A、
A、 B、
B、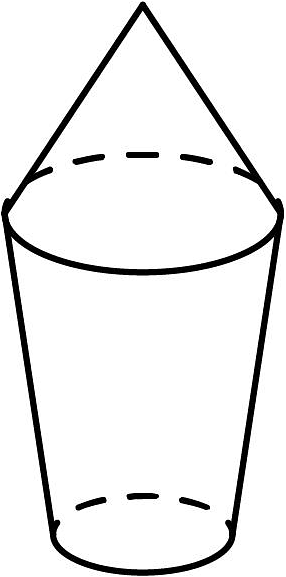 C、
C、 D、
D、
-
14、在圆的面积公式中,与的关系是( )A、一次函数关系 B、正比例函数关系 C、反比例函数关系 D、二次函数关系
-
15、下列方程是一元二次方程的是( )A、 B、 C、 D、
-
16、下面的图形是用数学家名字命名的,其中是中心对称图形的是( )A、
 科克曲线
B、
科克曲线
B、 笛卡尔心形图
C、
笛卡尔心形图
C、 希尔伯特曲线
D、
希尔伯特曲线
D、 斐波那契螺旋线
斐波那契螺旋线
-
17、若边长为6的正方形绕点A顺时针旋转,得正方形 , 记旋转角为α.
 (1)、如图1,当时,求点C经过弧的长度和线段扫过的扇形面积;(2)、如图2,当时,与的交点为E,求线段的长度;(3)、如图3,在旋转过程中,若F为线段的中点,求线段长度的取值范围.
(1)、如图1,当时,求点C经过弧的长度和线段扫过的扇形面积;(2)、如图2,当时,与的交点为E,求线段的长度;(3)、如图3,在旋转过程中,若F为线段的中点,求线段长度的取值范围. -
18、如图,分别与相切于点A,B,点M在上,且 , , 垂足为N.
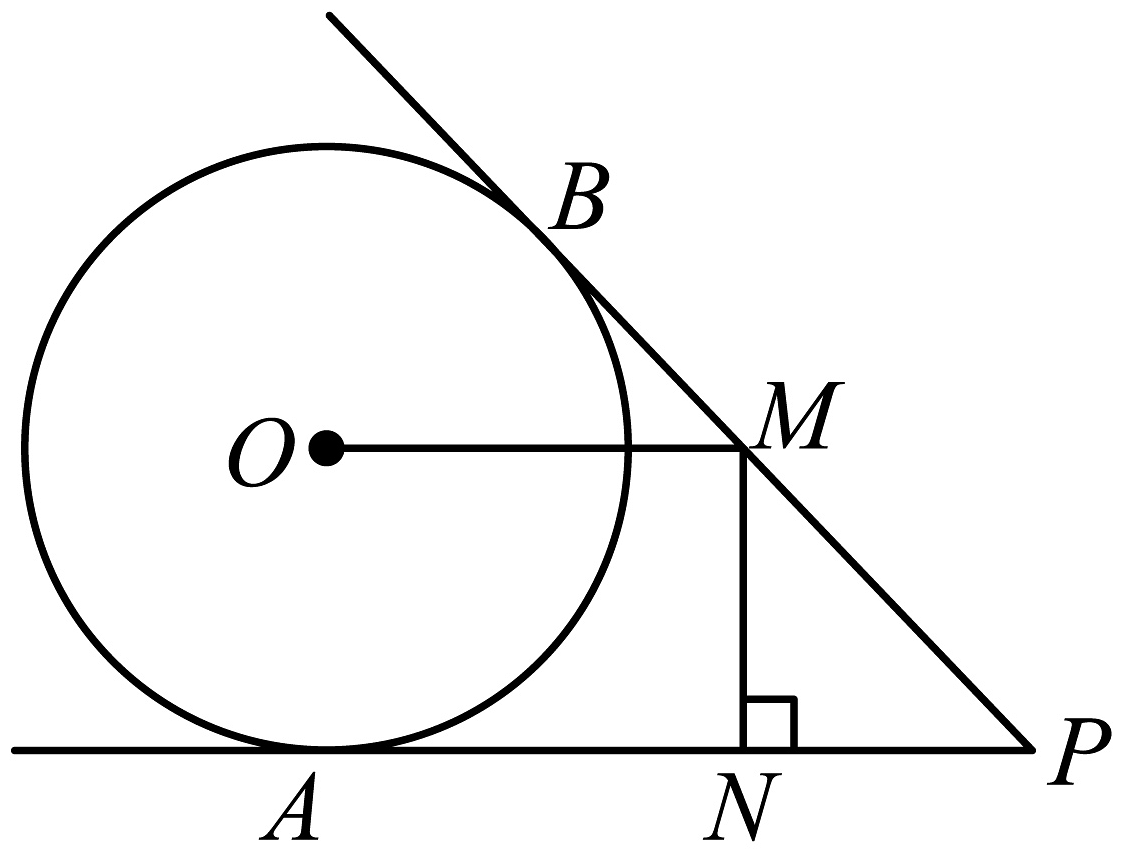 (1)、求证:;(2)、若的半径 , , 求的长.
(1)、求证:;(2)、若的半径 , , 求的长. -
19、已知圆锥的底面半径为 , 高 , 现有一只蚂蚁从底边上一点A出发,在侧面上爬行一周后又回到A点.
 (1)、求圆锥的全面积;(2)、求蚂蚁爬行的最短距离.
(1)、求圆锥的全面积;(2)、求蚂蚁爬行的最短距离. -
20、如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.
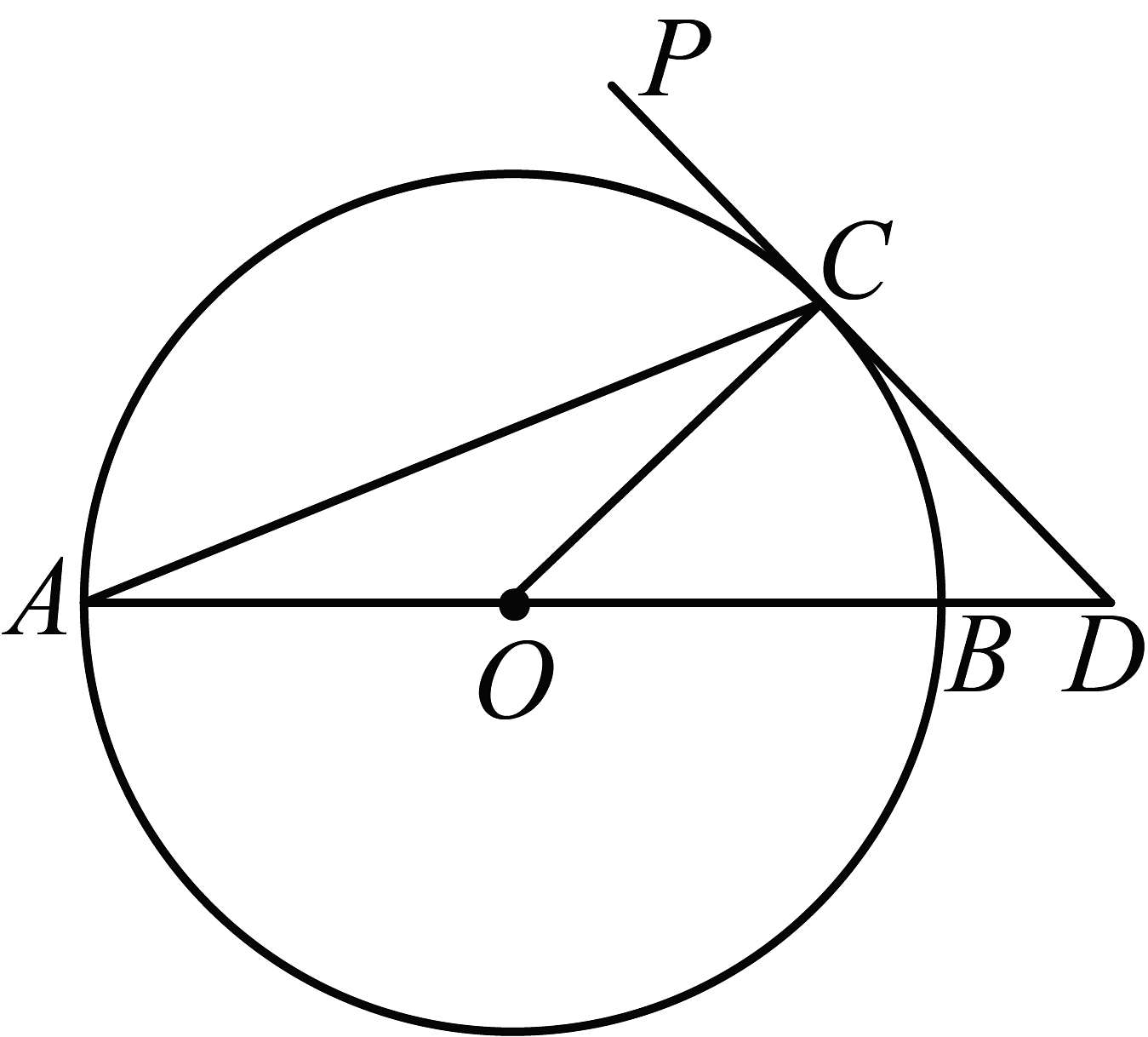
(1)求∠D的度数;
(2)若CD=2,求BD的长.