浙江省九年级上学期数学期中仿真模拟试题(二)
试卷更新日期:2025-09-18 类型:期中考试
一、选择题:本题共10小题,共30分.在每小题给出的选项中,只有一项是符合题目要求的.
-
1. 随着人们健康生活理念的提高,环保意识也不断增强,以下是回收、绿色包装、节水、低碳四个标志,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一元二次方程 中一次项系数、常数项分别是( )A、2, B、0, C、1, D、1,03. 抛物线的顶点坐标是( )A、 B、 C、 D、4. 下列各组中的四条线段成比例的是( )A、a=2,b=3,c=4,d=1 B、a=2, b= , c= , d= C、a=4,b=6,c=5,d=10 D、a= , b=3,c=2,d=5. 其居民为了减少外出,常使用手机软件在线上买菜,某买菜手机软件2020年1月的新注册用户人数为200万,3月的新注册用户人数为338万,则2、3两个月新注册用户人数每月的平均增长率是 ( )A、10% B、15% C、23% D、30%6. 如图,一个小孩坐在秋千上,若秋千绕点O旋转了 , 小孩的位置也从A点运动到了B点,则的度数为( )
2. 一元二次方程 中一次项系数、常数项分别是( )A、2, B、0, C、1, D、1,03. 抛物线的顶点坐标是( )A、 B、 C、 D、4. 下列各组中的四条线段成比例的是( )A、a=2,b=3,c=4,d=1 B、a=2, b= , c= , d= C、a=4,b=6,c=5,d=10 D、a= , b=3,c=2,d=5. 其居民为了减少外出,常使用手机软件在线上买菜,某买菜手机软件2020年1月的新注册用户人数为200万,3月的新注册用户人数为338万,则2、3两个月新注册用户人数每月的平均增长率是 ( )A、10% B、15% C、23% D、30%6. 如图,一个小孩坐在秋千上,若秋千绕点O旋转了 , 小孩的位置也从A点运动到了B点,则的度数为( ) A、 B、 C、 D、7. 如图,点A、B、C在上,为等边三角形,则的度数是( )
A、 B、 C、 D、7. 如图,点A、B、C在上,为等边三角形,则的度数是( ) A、60° B、50° C、40° D、30°8. 如图,当驾驶员的眼睛点与地面的距离为米时,是驾驶员的视觉盲区,车头近似的看成是矩形,且 , 若的长度为米,则车宽的长度大约是( )
A、60° B、50° C、40° D、30°8. 如图,当驾驶员的眼睛点与地面的距离为米时,是驾驶员的视觉盲区,车头近似的看成是矩形,且 , 若的长度为米,则车宽的长度大约是( )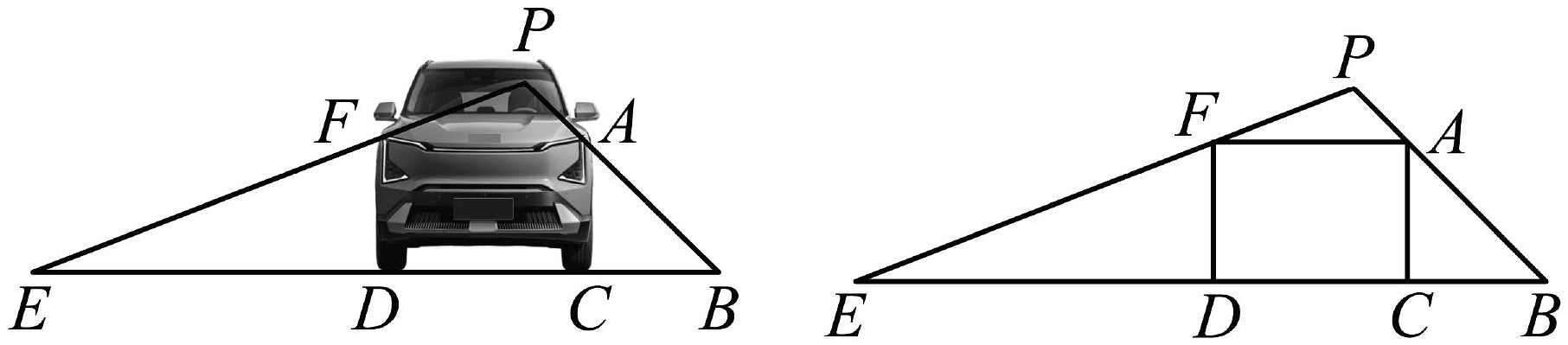 A、米 B、米 C、米 D、米9. 如图,在矩形ABCD中,AD>AB,AB=5cm,AC,BD交于点O,∠AOD=2∠AOB=120°,则BC=( )
A、米 B、米 C、米 D、米9. 如图,在矩形ABCD中,AD>AB,AB=5cm,AC,BD交于点O,∠AOD=2∠AOB=120°,则BC=( )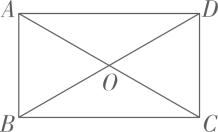 A、5cm B、cm C、cm D、cm10. 抛物线的顶点为 , 且经过点 , 其部分图象如图所示,则下列结论正确的是( )
A、5cm B、cm C、cm D、cm10. 抛物线的顶点为 , 且经过点 , 其部分图象如图所示,则下列结论正确的是( )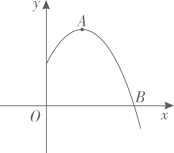 A、若抛物线经过点 , 则必过点 B、 C、若点和都在抛物线上,则 D、
A、若抛物线经过点 , 则必过点 B、 C、若点和都在抛物线上,则 D、二、填空题:本题共6小题,共18分.
-
11. 若关于的一元二次方程的一个根为 , 则的值为 .12. 已知实数 满足 ,则 的值为 .13. 如图,将绕点A逆时针旋转 , 得到 , 若点D在线段的延长线上,则的大小为 .
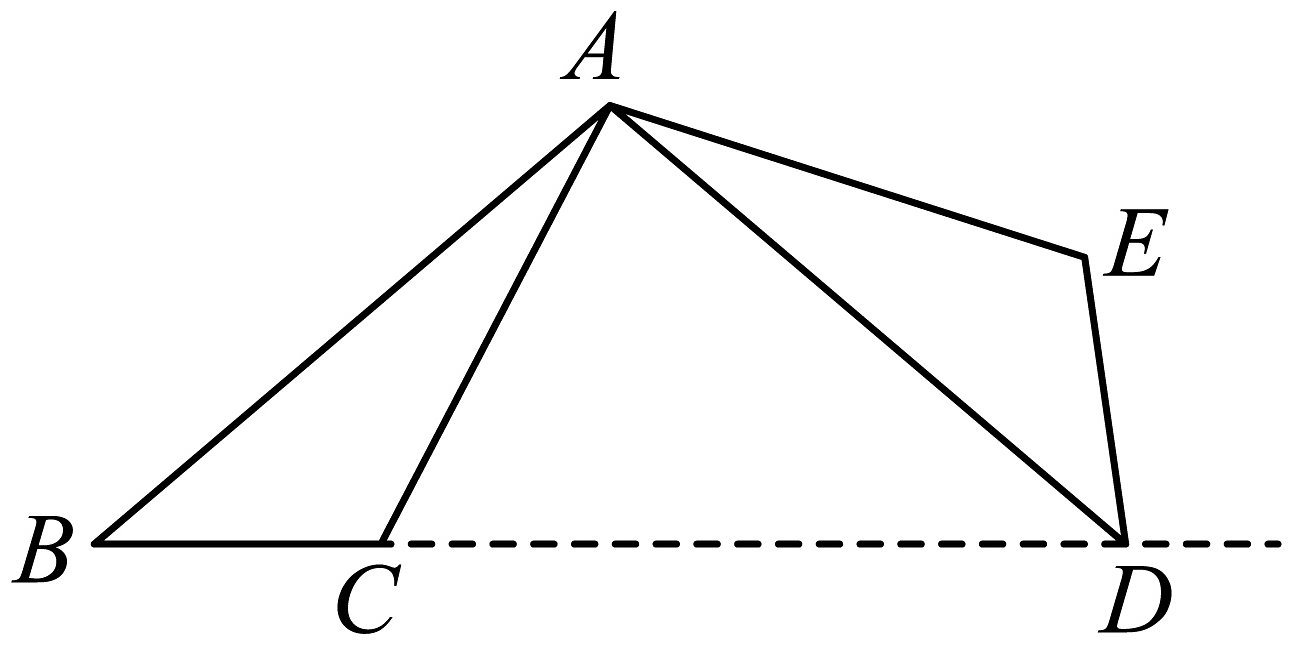 14. 如图,为的直径,弦于点 , , , 那么该圆的半径为.
14. 如图,为的直径,弦于点 , , , 那么该圆的半径为. 15. 如图,在平面直角坐标系中,将直角三角板的角的顶点与坐标原点O重合,直角顶点B在x轴的负半轴上,顶点A在第三象限.将绕点O逆时针旋转一定角度得到使点B的对应点落在边OA上.若 , 则点的坐标为 .
15. 如图,在平面直角坐标系中,将直角三角板的角的顶点与坐标原点O重合,直角顶点B在x轴的负半轴上,顶点A在第三象限.将绕点O逆时针旋转一定角度得到使点B的对应点落在边OA上.若 , 则点的坐标为 . 16. 如图,在▱ABCD中,AB=3,BC=4,∠B=60°,点E是AB边上一点,连接DE,过点E作EF⊥DE,交 BC边于点 F,且∠EFD=60°,则AE的长为.
16. 如图,在▱ABCD中,AB=3,BC=4,∠B=60°,点E是AB边上一点,连接DE,过点E作EF⊥DE,交 BC边于点 F,且∠EFD=60°,则AE的长为.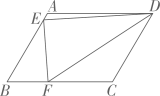
三、解答题(共8题,共72分)
-
17. 解下列方程:(1)、 .(2)、 .18. 如图,在以为直径的中,弦于点 , 与弦交于点 , 连接 , 已知 .
 (1)、求的半径.(2)、若 , 求的长.19. 已知 , , 求代数式的值.20. 已知二次函数y=mx2﹣2mx+3,其中m≠0.
(1)、求的半径.(2)、若 , 求的长.19. 已知 , , 求代数式的值.20. 已知二次函数y=mx2﹣2mx+3,其中m≠0.(1)若二次函数经过(﹣1,6),求二次函数解析式.
(2)若该抛物线开口向上,当﹣l≤x≤2时,抛物线的最高点为M,最低点为N,点M的纵坐标为6,求点M和点N的坐标.
(3)在二次函数图象上任取两点(x1 , y1),(x2 , y2),当a≤x1<x2≤a+2时,总有y1>y2 , 求a的取值范围.
21. 某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为),另外三面用栅栏围成,中间再用栅栏把它分成两个面积为的矩形,已知栅栏的总长度为 , 设较小矩形的宽为(如图),养殖场的总面积为 . (1)、求y关于x的函数关系式和自变量x的取值范围;(2)、当x为多少时,矩形养殖场的总面积最大?最大值为多少?22. 如图,四边形是平行四边形,相交于点O,E为的中点,连接 , 过点E作于点F,过点O作于点G.
(1)、求y关于x的函数关系式和自变量x的取值范围;(2)、当x为多少时,矩形养殖场的总面积最大?最大值为多少?22. 如图,四边形是平行四边形,相交于点O,E为的中点,连接 , 过点E作于点F,过点O作于点G. (1)、求证:四边形是矩形;(2)、若四边形是菱形, , 求的长.23. 如图1,由四个全等的直角三角形的直角边拼接成一个正方形 , 我们称这样的图形为“弦图”,“弦图”是中国古代数学的瑰宝,在如图2的“弦图”中,连结 , 交于点O,设与 , 的交点分别为M,N.吴老师和学生们对此“弦图”进行研究性学习时,有如下交流:
(1)、求证:四边形是矩形;(2)、若四边形是菱形, , 求的长.23. 如图1,由四个全等的直角三角形的直角边拼接成一个正方形 , 我们称这样的图形为“弦图”,“弦图”是中国古代数学的瑰宝,在如图2的“弦图”中,连结 , 交于点O,设与 , 的交点分别为M,N.吴老师和学生们对此“弦图”进行研究性学习时,有如下交流:吴老师:利用弦图中的三角形全等关系可证明“四边形是正方形,O是和的中点.”;
小聪:这两个结论都能证明,我还发现“”;
小颖:我发现“已知 , 的长度,就能确定的长度”,如:“已知 , , 求的长.”

结合上述师生的交流:
(1)、请你证明小聪发现的结论;(2)、请你解答小颖提出的问题“已知 , , 求的长.”24. 在一个圆中,圆心到该圆的任意一条弦的距离,叫做这条弦的弦心距. (1)、如图1,在中,半径是5,弦 , 则这条弦的弦心距长为 .(2)、通过大量的做题探究;小明发现:在同一个圆中,如果两条弦相等,那么这两条弦的弦心距也相等.但是小明想证明时却遇到了麻烦.请结合图2帮助小明完成证明过程如图2,在中, , , , 求证: .(3)、如图3,在中 , 的直径为20,且弦垂直于弦于 , 请应用上面得出的结论求的长.
(1)、如图1,在中,半径是5,弦 , 则这条弦的弦心距长为 .(2)、通过大量的做题探究;小明发现:在同一个圆中,如果两条弦相等,那么这两条弦的弦心距也相等.但是小明想证明时却遇到了麻烦.请结合图2帮助小明完成证明过程如图2,在中, , , , 求证: .(3)、如图3,在中 , 的直径为20,且弦垂直于弦于 , 请应用上面得出的结论求的长.