-
1、计算: .
-
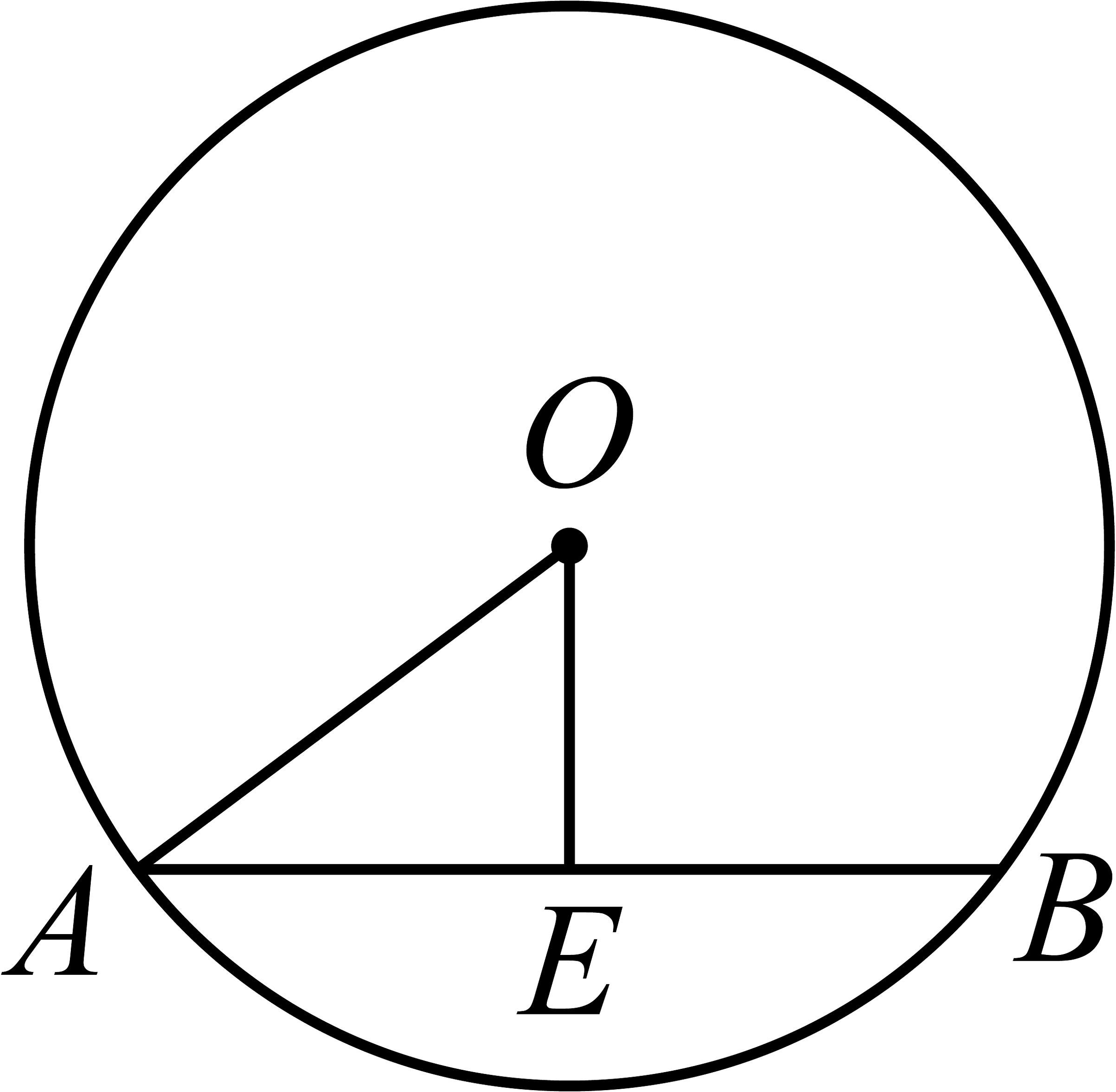
2、如图,于 , 若的半径为 , , 则 .
-
3、函数的图象在每个象限内随的增大而增大,则的取值范围是 .
-
4、已知与关于原点对称,则的值是 .
-
5、如图,在的正方形网格中,每个小正方形的边长都是1,的顶点都在正方形顶点上,那么的值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
6、已知 , 相似比为 , 若的周长是9,则的周长为( ).A、1 B、3 C、6 D、9
-
7、若零下2摄氏度记为 , 则零上2摄氏度记为( ).A、 B、 C、 D、
-
8、在△ABC中,点H为垂心.(1)、证明正弦定理.(2)、证明:.
-
9、已知方程(m+1)x2+2x-5m-13=0的根均为整数,求实数m的值.
-
10、一个人在直角坐标系上从(-3,-3)走到(3,3),每次他可以往上走一个单位长度或往右走一个单位长度且它的横坐标和纵坐标的绝对值至少有一个大于等于二,则这个人有种走法.
-
11、已知E为正方形ABCD的边BC延长线上一点,以AE为边作正方形AEFG,使得A、G两点在BE的同侧,BD的延长线与AF交于点H.若HD= , FH=5 , 则BE的长为.
-
12、若关于x的方程(x2-1)(kx2-6x-8)=0有三个不同的实数解,则k的个数为.
-
13、已知 , , 且 , 则=.
-
14、.
-
15、已知x,y,z为正整数,且 , 则满足的(x,y,z)有组.
-
16、已知a和b由抛骰子得到(等概率抛到1,2,3,4,5,6),则方程(a-1)x2+(b-2)x+1=0有实数解的概率为.
-
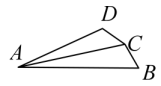
17、如图,在凸四边形ABCD中,AB>AD,BC=CD,AC平分∠BAC,∠BAD=25°,则∠BCD=.
-
18、已知是的因式,则
-
19、定义a*b=3a-b,若2*(5-x)=1,则x=.
-
20、我们不妨约定:对角互补的凸四边形叫做“互补四边形”.根据约定,解答下列问题.
 (1)、试判断下列图形一定为“互补四边形”?若是,请在括号内划“”;若不是,请在括号内划“”.
(1)、试判断下列图形一定为“互补四边形”?若是,请在括号内划“”;若不是,请在括号内划“”.①平行四边形( );②矩形( );③正方形( ).
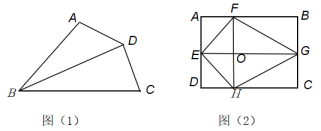
(2)、如图(1),在四边形中,对角线平分∠ABC,DA=DC,AB<CB.求证:四边形是“互补四边形”.(3)、如图(2),若□ABCD是“互补四边形”,点是□ABCD内部一个动点,且不与四边重合,过动点作的平行线,交□ABCD的边于点连接 , AB=8,AD=6.当点运动时,求四边形周长的最小值.