2.3《用频率估计概率》—浙教版数学九年级上册课堂分层训练

试卷更新日期：2025-09-18 类型：同步测试

进入出卷网下载

一、基础应用

1. 数学家皮尔逊为了研究概率问题，进行了大量重复抛硬币试验，并用频率来估计概率，当他把一枚硬币抛掷 24000次时，则下列正面朝上的次数与该实验结果比较符合的是（）

A、11011 B、12012 C、13013 D、14014

查看试题解析
2. 在一个不透明的箱子里装有 $m$ 个球，其中红球4个，这些球除颜色外都相同，每次将球搅拌均匀后，任意摸出一个球记下颜色后再放回，大量重复试验后发现，摸到红球的频率在 $0.5$ ，那么可以估算出 $m$ 的值为（）

A、8 B、12 C、15 D、20

查看试题解析
3. 在学习了“用频率估计概率”这一节内容后，某课外兴趣小组利用计算器进行模拟试验来探究“6个人中有2个人同月过生日的概率”，他们将试验中获得的数据记录如下：
试验次数
100
300
500
1000
1600
2000
“有2个人同月过生日”的次数
80
229
392
779
1251
1562
“有2个人同月过生日”的频率
0.8
0.763
0.784
0.779
0.782
0.781
通过试验，该小组估计“6个人中有2个人同月过生日”的概率（精确到0.01）大约是（）

A、0.80 B、0.79 C、0.78 D、0.77

查看试题解析
4. 某地区林业局考察一种树苗移植的成活率，将调查数据绘制成统计图，则可估计这种树苗移植成活的概率约是（　）

A、 $0.80$ B、 $0.85$ C、 $0.90$ D、 $0.95$

查看试题解析
5. 若某随机事件发生的概率为 $\frac{1}{2}$ ，则下列说法正确的是（）

A、在2次试验中，该事件至少发生1次 B、在1000次试验中，该事件发生的次数一定为500次 C、随着试验次数的增加，该事件发生的频率会逐渐稳定在 $\frac{1}{2}$ D、当试验次数特别多时，该事件发生的频率为 $\frac{1}{2}$

查看试题解析
6. 在相同条件下对某品种绿豆进行发芽试验，得到如下的数据：
每批粒数 $n$
100
300
400
600
1000
2000
3000
发芽的粒数 $m$
96
282
382
570
949
1902
2850
发芽频率
$\begin{array}{l} 0.960 \end{array}$
$\begin{array}{l} 0.940 \end{array}$
$\begin{array}{l} 0.955 \end{array}$
$\begin{array}{l} 0.950 \end{array}$
$\begin{array}{l} 0.949 \end{array}$
$\begin{array}{l} 0.951 \end{array}$
$\begin{array}{l} 0.950 \end{array}$
则估计这种绿豆的发芽概率是．

查看试题解析
7. 为了估计抛掷同一枚瓶盖落地后凸面向上的概率，小明做了大量重复试验．经过统计得到凸面向上的频率稳定在 $0.45$ ，凸面向下的频率稳定在 $0.55$ ，由此可估计抛掷瓶盖落地后凸面向上的概率约为．

查看试题解析
8. 在一个不透明的袋子里装有红球和黄球，共有20个球，这些球除颜色不同外其余均相同，每次从袋子中摸出一个球记录下颜色后再放回，经过很多次重复试验，发现摸到黄球的频率稳定在 $0.65$ ，则袋中黄球有个．

查看试题解析
9. 盒中有若干枚黑棋和白棋，这些棋除颜色外无其他差别，现让学生进行摸棋试验：每次摸出一枚棋，记录颜色后放回摇匀．重复进行这样的试验得到以下数据：
摸棋的次数n
100
200
300
500
800
1000
摸到黑棋的次数m
24
51
76
124
201
250
摸到黑棋的频率 $\frac{m}{n}$ （精确到0.001）
0.240
0.255
0.253
0.248
0.251
0.250
（1）根据表中数据估计从盒中摸出一枚棋是黑棋的概率是　　；（精确到0.01）
（2）若盒中黑棋与白棋共有4枚，某同学一次摸出两枚棋，请计算这两枚棋颜色不同的概率，并说明理由

查看试题解析

二、能力提升

10. 如图，一个转盘由黑、白两色组成，小明自由转动转盘，记下指针所在区域的颜色，不断重复自由转动转盘n次，下表是小明记录“指针落在黑色区域”的频数、频率统计表．
自由转动转盘n次
100
300
500
1500
3000
…
指针落在黑色区域的频数m
23
78
125
375
750
…
指针落在黑色区域的频率p
$0.23$
$0.26$
$0.25$
$0.25$
$0.25$
$\dots$

(1)、观察上表，求黑色扇形圆心角的度数．

(2)、如果小明让转盘自由转动一次，指针恰好落在黑色区域，小明可以获赠一份小礼物，求小明获赠小礼物的概率．

查看试题解析
11. 种子被称作农业的“芯片”，关系到国家粮食安全．某种业公司培育成功了 $A ， B$ 两种新玉米种子，为了了解它们的出芽情况，在推广前做了五次出芽实验，每次随机各自取相同种子数，在相同的培有环境中分别实验，实验情况记录如下：
种子数量 200 500 800 1500 3000
A 出芽率 0.98 0.94 0.96 0.98 0.97
B 出芽率 0.98 0.95 0.94 0.97 0.96
下面在三个推断：
①当实验种子数员为200时，两种种子的出芽率均为0.98，所以 $A ， B$ 两种新五米种子出芽的概率一样；
②随着实验种子数量的增加， $B$ 种子出芽率在0.96附近摆动，显示出一定的稳定性，可以估计 $B$ 种子出芽的概率是0.96：
③在同样的地质环境下播种， $A$ 种子的出芽率可能会离于 $B$ 种子．
其中合理的是（）

A、①②③ B、①② C、②③ D、①③

查看试题解析
12. 某小组做“当试验次数很大时，用频率估计概率”的试验时，统计了某一结果出现的频率，表格如下，则符合这一结果的试验最有可能是（）
次数
$100$
$200$
$300$
$400$
$500$
$600$
$700$
$800$
$900$
$1000$
e频率
$0.60$
$0.30$
$0.50$
$0.36$
$0.42$
$0.38$
$0.41$
$0.39$
$0.40$
$0.40$

A、掷一个质地均匀的骰子，向上的面点数是“6” B、掷一枚一元的硬币，正面向上 C、在一个不透明的袋子里有2个红球和3个黄球，它们除了颜色外都相同，从中任取一球是红球 D、有三张扑克牌，分别是3，5，5，背面朝上洗匀后，随机抽出一张是5

查看试题解析
13. 某小组在“用频率估计概率”的实验中，统计了某种结果出现的频率，绘制了如图所示的折线统计图，那么符合这一结果的实验最有可能的是（）

A、掷一枚质地均匀的硬币，落地时结果是“正面向上” B、掷一个质地均匀的正六面体骰子，落地时朝上的面点数是 $6$ C、在“石头、剪刀、布”的游戏中，小明随机出的是“石头” D、袋子中有 $1$ 个白球和 $2$ 个黄球，只有颜色上的区别，从中随机取出一个球是黄球

查看试题解析
14. 为了解某地区1000名九年级男生的身高数据，统计结果如下：
身高 $x / cm$
$x < 160$
$160 \leq x < 170$
$170 \leq x < 180$
$x \geq 180$
人数
59
261
557
123
根据统计，随机抽取该地区一名九年级男生，估计他的身高不低于 $170 c m$ 的概率是（）

A、0.32 B、0.55 C、0.68 D、0.87

查看试题解析
15. 做任意抛掷一只纸杯的重复试验，获得如下数据：
抛掷总次数
50
100
500
800
1500
3000
5000
杯口朝上频数
5
15
100
168
330
660
1100
杯口朝上频率
0.1
0.15
0.2
0.21
0.22
0.22
0.22
估计任意抛掷一只纸杯的杯口朝上的概率为（结果精确到0.1）

查看试题解析
16. 一个不透明的箱子里装有n个球，其中红球有5个，这些球除颜色外都相同．每次将球搅拌均匀后，任意摸出一个球记下颜色后再放回．大量重复试验后发现，摸到红球的频率稳定在0.25，那么可以估算出n的值为．

查看试题解析
17. 某学习小组做“用频率估计概率”的摸球试验：在不透明的盒子中装入红色、蓝色的玻璃球共 $60$ 个，从中随机摸出一个球，记下颜色后放回，统计了“摸出球为红色”出现的频率，绘制了如图的折线统计图，那么估计盒子中装入红色球的个数约为．

查看试题解析
18. 在一个不透明的口袋里装有颜色不同的红、白两种颜色的球共5个，某学习小组做摸球试验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复，如表是活动进行中的一组统计数据：
摸球的次数 $n$
100
150
200
500
800
1000
摸到白球的次数 $m$
59
96
116
295
484
601
摸到白球的频率 $\frac{m}{n}$
$0.59$
$0.64$
$0.58$
$0.59$
$0.605$
$0.601$

(1)、请估计：当 $n$ 很大时，摸到白球的频率将会接近______；（精确到 $0.1$ ）

(2)、试估算口袋中红球有多少个？

(3)、请画树状图或列表计算：从中先摸出一球，不放回，再摸出一球，这两个球颜色不同的概率是多少？

查看试题解析
19. 有一个圆形转盘，分黑色、白色两个区域．

(1)、某人转动转盘，对指针落在黑色区域或白色区域进行了大量试验，得到数据如下表：
实验次数n（次）
10
100
2000
5000
10000
50000
100000
白色区域次数m（次）
3
34
680
1600
3405
16500
33000
落在白色区域频率 $\frac{m}{n}$
0.3
0.34
0.34
0.32
0.34
0.33
0.33
请你利用上述实验，估计转动该转盘指针落在白色区域的概率为___________．

(2)、若该圆形转盘白色扇形的圆心角为 $120 °$ ，黑色扇形的圆心角为 $240 °$ ，转动转盘两次，请用画树状图或列表的方法求指针一次落在白色区域，另一次落在黑色区域的概率．

查看试题解析
20. 某水果公司以9元/千克的成本从果园购进10000千克特级柑橘，在运输过程中，有部分柑橘损坏，该公司对刚运到的特级柑橘进行随机抽查，并得到如下的“柑橘损坏率”统计图．由于市场调节，特级柑橘的售价与日销售量之间有一定的变化规律，如下表是近一段时间该水果公司的销售记录．
特级柑橘的售价(元/千克)
14
15
16
17
18
特级柑橘的日销售量(千克)
1000
950
900
850
800

(1)、估计购进的10000千克特级柑橘中完好的柑橘的总重量为________千克；

(2)、按此市场调节的规律来看，若特级柑橘的售价定为 $16.5$ 元每千克，估计日销售量，并说明理由．

(3)、考虑到该水果公司的储存条件，该公司打算12天内售完这批特级柑橘（只售完好的柑橘），且售价保持不变，求该公司每日销售该特级柑橘可能达到的最大利润，并说明理由．

查看试题解析

三、综合拓展

21. 对一批衬衣进行抽检，统计合格衬衣的件数，获得如下频数表.

抽取件数（件）	100	150	200	500	800	1000
合格频数	88	141	176	445	720	900
合格频率	______	0.94	0.88	0.89	0.90	______

(1)、完成上表.

(2)、估计任意抽一件衬衣是合格品的概率.

(3)、估计出售1200件衬衣，其中次品大约有几件.

查看试题解析

22. 某水果公司以9元/千克的成本从果园购进10000千克特级柑橘，在运输过程中，有部分柑橘损坏，该公司对刚运到的特级柑橘进行随机抽查，并得到如下的“柑橘损坏率”统计图．由于市场调节，特级柑橘的售价与日销售量之间有一定的变化规律，如下表是近一段时间该水果公司的销售记录．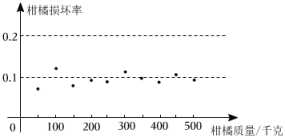
特级柑橘的售价(元/千克) 14 15 16 17 18
特级柑橘的日销售量(千克) 1000 850 900 850 800

(1)、估计购进的10000千克特级柑橘中完好的柑橘的总重量为千克；

(2)、按此市场调节的规律来看，若特级柑橘的售价定为16.5元每千克，估计日销售量，并说明理由．

(3)、考虑到该水果公司的储存条件，该公司打算12天内售完这批特级柑橘 $($ 只售完好的柑橘 $)$ ，且售价保持不变，求该公司每日销售该特级柑橘可能达到的最大利润，并说明理由．

查看试题解析

试验次数	100	300	500	1000	1600	2000
“有2个人同月过生日”的次数	80	229	392	779	1251	1562
“有2个人同月过生日”的频率	0.8	0.763	0.784	0.779	0.782	0.781

每批粒数 $n$	100	300	400	600	1000	2000	3000
发芽的粒数 $m$	96	282	382	570	949	1902	2850
发芽频率	$\begin{array}{l} 0.960 \end{array}$	$\begin{array}{l} 0.940 \end{array}$	$\begin{array}{l} 0.955 \end{array}$	$\begin{array}{l} 0.950 \end{array}$	$\begin{array}{l} 0.949 \end{array}$	$\begin{array}{l} 0.951 \end{array}$	$\begin{array}{l} 0.950 \end{array}$

摸棋的次数n	100	200	300	500	800	1000
摸到黑棋的次数m	24	51	76	124	201	250
摸到黑棋的频率 $\frac{m}{n}$ （精确到0.001）	0.240	0.255	0.253	0.248	0.251	0.250

自由转动转盘n次	100	300	500	1500	3000	…
指针落在黑色区域的频数m	23	78	125	375	750	…
指针落在黑色区域的频率p	$0.23$	$0.26$	$0.25$	$0.25$	$0.25$	$\dots$

种子数量		200	500	800	1500	3000
A	出芽率	0.98	0.94	0.96	0.98	0.97
B	出芽率	0.98	0.95	0.94	0.97	0.96

次数	$100$	$200$	$300$	$400$	$500$	$600$	$700$	$800$	$900$	$1000$
e频率	$0.60$	$0.30$	$0.50$	$0.36$	$0.42$	$0.38$	$0.41$	$0.39$	$0.40$	$0.40$

身高 $x / cm$	$x < 160$	$160 \leq x < 170$	$170 \leq x < 180$	$x \geq 180$
人数	59	261	557	123

抛掷总次数	50	100	500	800	1500	3000	5000
杯口朝上频数	5	15	100	168	330	660	1100
杯口朝上频率	0.1	0.15	0.2	0.21	0.22	0.22	0.22

摸球的次数 $n$	100	150	200	500	800	1000
摸到白球的次数 $m$	59	96	116	295	484	601
摸到白球的频率 $\frac{m}{n}$	$0.59$	$0.64$	$0.58$	$0.59$	$0.605$	$0.601$

实验次数n（次）	10	100	2000	5000	10000	50000	100000
白色区域次数m（次）	3	34	680	1600	3405	16500	33000
落在白色区域频率 $\frac{m}{n}$	0.3	0.34	0.34	0.32	0.34	0.33	0.33

特级柑橘的售价(元/千克)	14	15	16	17	18
特级柑橘的日销售量(千克)	1000	950	900	850	800

特级柑橘的售价(元/千克)	14	15	16	17	18
特级柑橘的日销售量(千克)	1000	850	900	850	800

2.3《 用频率估计概率》—浙教版数学九年级上册课堂分层训练

一、基础应用

二、能力提升

三、综合拓展

2.3《用频率估计概率》—浙教版数学九年级上册课堂分层训练