浙江省九年级上学期数学期中仿真模拟试题(三)
试卷更新日期:2025-09-18 类型:期中考试
一、选择题(本大题有10题,每题3分,共30分.在每题列出的四个选项中只有一个是符合题目要求的,不选、多选、错选均不得分.)
-
1. 下列函数中,是的二次函数的是( )A、 B、 C、 D、2. 已知 则下列等式中,不成立的是( )A、 B、 C、 D、4x=3y3. 已知⊙O的半径为5,点P在⊙O外,则OP的长可能是( )A、3 B、4 C、5 D、64. 二次函数的图象如图所示,则点位于( )
 A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,已知为的直径,弦与交于点E,连结 , 设 , 则( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,已知为的直径,弦与交于点E,连结 , 设 , 则( ) A、 B、 C、 D、6. 已知点 , , 都在二次函数的图象上,则 , , 的大小关系为( )A、 B、 C、 D、7. 如图,在中, , 点在AB边上,连结CD,点是CD的中点,连结AE.若 , 则AE的长是( )
A、 B、 C、 D、6. 已知点 , , 都在二次函数的图象上,则 , , 的大小关系为( )A、 B、 C、 D、7. 如图,在中, , 点在AB边上,连结CD,点是CD的中点,连结AE.若 , 则AE的长是( )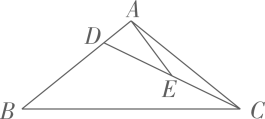 A、2 B、 C、 D、8. 如图,点 , 在半圆上, , 相交于点 , 则的值为( )
A、2 B、 C、 D、8. 如图,点 , 在半圆上, , 相交于点 , 则的值为( ) A、 B、 C、 D、9. 已知正比例函数与二次函数的图象相交于两点.若两点的横坐标分别为 , 则的值为( )A、 B、 C、 D、10. 如图,在半圆O中,直径 , C,D是半圆上两点,P是直径上一点,若 , , 则的最小值为( )
A、 B、 C、 D、9. 已知正比例函数与二次函数的图象相交于两点.若两点的横坐标分别为 , 则的值为( )A、 B、 C、 D、10. 如图,在半圆O中,直径 , C,D是半圆上两点,P是直径上一点,若 , , 则的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题有6题,每题3分,共18分.)
-
11. 一个多边形的内角和是720°,则这个多边形的边数是。12. 如图,在的正方形网格纸中,每个小正方形的边长均为1,点O,A,B为格点,即是小正方形的顶点,若将扇形围成一个圆锥,则这个圆锥的底面圆的半径为 .
 13. 《九章算术》是我国古代数学成就的杰出代表,其中《方田》章给出计算弧田面积所用公式为:弧田面积(弦矢+矢),弧田(如图)是由圆弧和其所对的弦所围成,公式中“弦”指圆弧所对弦长 , “矢”等于半径长与圆心到弦的距离之差.在如图所示的弧田中,“弦”为8,“矢”为2,则的值为 .
13. 《九章算术》是我国古代数学成就的杰出代表,其中《方田》章给出计算弧田面积所用公式为:弧田面积(弦矢+矢),弧田(如图)是由圆弧和其所对的弦所围成,公式中“弦”指圆弧所对弦长 , “矢”等于半径长与圆心到弦的距离之差.在如图所示的弧田中,“弦”为8,“矢”为2,则的值为 . 14. 若时,函数的最大值为17,则 .15. 如图,△ABC 为直角三角形,∠ACB=90°,AC=1,BC=3,D 是 AB 边上的中点,将△ACB 绕着点 A 逆时针旋转,使点 C 落在线段 CD 上的点 E 处,点 B 的对应点为 F,边 EF 与边 AB 交于点 G, 则 DG 的长 .
14. 若时,函数的最大值为17,则 .15. 如图,△ABC 为直角三角形,∠ACB=90°,AC=1,BC=3,D 是 AB 边上的中点,将△ACB 绕着点 A 逆时针旋转,使点 C 落在线段 CD 上的点 E 处,点 B 的对应点为 F,边 EF 与边 AB 交于点 G, 则 DG 的长 . 16. 已知函数(是常数,),(是常数,),在同一平面直角坐标系中,若无论为何值,函数和的图象总有公共点,则的取值范围是 .
16. 已知函数(是常数,),(是常数,),在同一平面直角坐标系中,若无论为何值,函数和的图象总有公共点,则的取值范围是 .三、解答题(本大题有8题,第17~21题每题8分,第22、23题每题10分,第24题12分,共72分.)
-
17. 抛物线y=-x2+(m-1)x+m与y轴交于点(0,3).(1)、求出m的值及抛物线与x轴的交点坐标.(2)、当x取什么值时,抛物线在x轴下方?(3)、当x取什么值时,y的值随x的增大而增大.18. 如图,是的角平分线,在边上取点 , 使 .
 (1)、求证: .(2)、若 , , 求的度数.19. 某工厂为了对新研发的一种产品进行合理定价,将该产品按拟定的价格进行试销,通过对5天的试销情况进行统计,得到如下数据:
(1)、求证: .(2)、若 , , 求的度数.19. 某工厂为了对新研发的一种产品进行合理定价,将该产品按拟定的价格进行试销,通过对5天的试销情况进行统计,得到如下数据:单价(元/件)
30
34
38
40
42
销量(件)
40
32
24
20
16
(1)、分析表格中的数据发现销量y与单价x之间存在一次函数关系,求y关于x的函数关系式.(2)、若该产品的成本是20元/件,为使工厂获得最大利润,该产品的单价应定为多少?20. 根据要求作图并证明. (1)、如图,请按以下步骤进行尺规作图,并保留作图痕迹:
(1)、如图,请按以下步骤进行尺规作图,并保留作图痕迹:①画一条直径;
②作的垂直平分线交于点C,D;
③连结 , 得到 .
(2)、根据第(1)小题作法,给出是等边三角形的证明.21. 如图,某跳水运动员进行10米跳台跳水训练,水面边缘点C的坐标为 . 运动员(将运动员看成一点)在空中运动的路线是经过原点O的抛物线.在跳某个规定动作时,运动员在空中最高处A点的坐标为 , 正常情况下,运动员在距水面高度5米以前,必须完成规定的翻腾、打开动作,并调整好入水姿势,否则就会失误. (1)、求运动员在空中运动时对应抛物线的解析式并求出入水处B点的坐标;(2)、若运动员在空中调整好入水姿势时,恰好距点C的水平距离为5米,问该运动员此次跳水会不会失误?通过计算说明理由.
(1)、求运动员在空中运动时对应抛物线的解析式并求出入水处B点的坐标;(2)、若运动员在空中调整好入水姿势时,恰好距点C的水平距离为5米,问该运动员此次跳水会不会失误?通过计算说明理由.

