浙教版数学八年级上学期期中模拟评估卷(一)
试卷更新日期:2025-09-19 类型:期中考试
一、选择题(本大题有10个小题,每小题3分,共 30分)
-
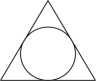
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、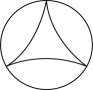 D、
D、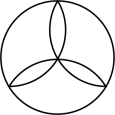 2. 普通家用人字梯一般都会在两旁分别设计一根“拉杆”,这样设计是利用( )
2. 普通家用人字梯一般都会在两旁分别设计一根“拉杆”,这样设计是利用( ) A、两点之间,线段最短 B、垂线段最短 C、三角形具有稳定性 D、四边形具有不稳定性3. 下列各组线段中,首尾相接不能组成三角形的是( )A、12cm,8cm,5cm B、12cm,8cm,6cm C、12cm,5cm,6cm D、8cm,5cm,6cm4. 已知在 Rt△ABC 中,斜边上的中线 CD=5cm,则斜边 AB的长为( )A、5 B、6 C、8 D、105. 在等腰三角形ABC中,若∠A=70°,则∠B的度数是( )A、40° B、55° C、70° D、40°或55°或70°6. 如图, , , , 三点在一条直线上,下面结论不一定正确的是( )
A、两点之间,线段最短 B、垂线段最短 C、三角形具有稳定性 D、四边形具有不稳定性3. 下列各组线段中,首尾相接不能组成三角形的是( )A、12cm,8cm,5cm B、12cm,8cm,6cm C、12cm,5cm,6cm D、8cm,5cm,6cm4. 已知在 Rt△ABC 中,斜边上的中线 CD=5cm,则斜边 AB的长为( )A、5 B、6 C、8 D、105. 在等腰三角形ABC中,若∠A=70°,则∠B的度数是( )A、40° B、55° C、70° D、40°或55°或70°6. 如图, , , , 三点在一条直线上,下面结论不一定正确的是( ) A、 B、 C、 D、7. 若证明命题: “对于任意实数 恒成立”是假命题,只需要举一个反例,则这个反例可以是( )A、 B、 C、 D、8. 如图,已知在△ABC中,∠BAC=50°,∠ACB=54°,敏敏通过尺规作图得到AM,DN交于点O,连接OC,根据其作图痕迹,可得∠OCB 的度数为( )
A、 B、 C、 D、7. 若证明命题: “对于任意实数 恒成立”是假命题,只需要举一个反例,则这个反例可以是( )A、 B、 C、 D、8. 如图,已知在△ABC中,∠BAC=50°,∠ACB=54°,敏敏通过尺规作图得到AM,DN交于点O,连接OC,根据其作图痕迹,可得∠OCB 的度数为( ) A、25° B、27° C、29° D、31°9. 如图,在Rt△ABC中,∠A=90°,∠C=60°,点D,E分别在AC,BC边上,将∠C沿直线DE折叠,点C恰好落在AB边上的点 F处,且DF平分∠ADE,若BC=9,则CD的长为 ( )
A、25° B、27° C、29° D、31°9. 如图,在Rt△ABC中,∠A=90°,∠C=60°,点D,E分别在AC,BC边上,将∠C沿直线DE折叠,点C恰好落在AB边上的点 F处,且DF平分∠ADE,若BC=9,则CD的长为 ( ) A、6 B、5 C、4 D、310. 如图①的图案称“赵爽弦图”,是我国汉代数学家赵爽在注解《周髀算经》时给出的,它由四个全等的直角三角形围成一个大正方形,中间是个小正方形,我们在此图形中连结四条线段得到如图②的图案,记阴影部分的面积为 , 空白部分的面积为 , 若 , 则大正方形的边长与小正方形的边长的比值为( )
A、6 B、5 C、4 D、310. 如图①的图案称“赵爽弦图”,是我国汉代数学家赵爽在注解《周髀算经》时给出的,它由四个全等的直角三角形围成一个大正方形,中间是个小正方形,我们在此图形中连结四条线段得到如图②的图案,记阴影部分的面积为 , 空白部分的面积为 , 若 , 则大正方形的边长与小正方形的边长的比值为( )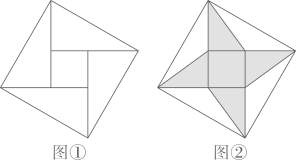 A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题(本题有8个小题,每小题3分,共24分)
-
11. “等边三角形中有一个内角等于60°”的的逆命题是 , 这个逆命题(填“成立”或“不成立”).12. 如图,是一块直角三角板,其中 , .直尺的一边经过顶点A , 若 , 则的度数为.
 13. 如图,已知在△ABC中,CD是AB边上的高,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于 .
13. 如图,已知在△ABC中,CD是AB边上的高,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于 . 14. 如图,△ABC中.点D在BC边上,BD=AD=AC,E为CD的中点.若∠CAE=16°,则∠B为度.
14. 如图,△ABC中.点D在BC边上,BD=AD=AC,E为CD的中点.若∠CAE=16°,则∠B为度. 15. 如图,在△ABC中,AB=BC,在BC上取点M,在MC上取点N,使MN=NA,若∠BAM=∠NAC,则∠MAC=.
15. 如图,在△ABC中,AB=BC,在BC上取点M,在MC上取点N,使MN=NA,若∠BAM=∠NAC,则∠MAC=.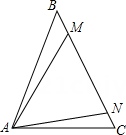 16. 如图,在△ABC中,AD 是BC 边上的中线.若S△ABC=12,AC=3,则点 D到AC的距离为.
16. 如图,在△ABC中,AD 是BC 边上的中线.若S△ABC=12,AC=3,则点 D到AC的距离为. 17. 如图,在△ABC中,∠A=90°,AB=6,BC=10,BC的垂直平分线分别交AC,BC于点D,E,则AD的长为.
17. 如图,在△ABC中,∠A=90°,AB=6,BC=10,BC的垂直平分线分别交AC,BC于点D,E,则AD的长为. 18. 如图2是某款台灯(图 1)的示意图,处于水平位置的棤杆 E F 可以绕着点 转动,当 O F 分别转到 O M, O N 的位置时, 测得 , 点 M, N 的高度差为 , 点 , 的水平距离 , 点 M, F 的水平距离 , 若该台灯的底座高度 , 垂直于底座的灯柱长 O A 与 O F 长度一样,从 点射出的光线与桌面成 ,则光线所照区域最大范围 B P 为 cm .
18. 如图2是某款台灯(图 1)的示意图,处于水平位置的棤杆 E F 可以绕着点 转动,当 O F 分别转到 O M, O N 的位置时, 测得 , 点 M, N 的高度差为 , 点 , 的水平距离 , 点 M, F 的水平距离 , 若该台灯的底座高度 , 垂直于底座的灯柱长 O A 与 O F 长度一样,从 点射出的光线与桌面成 ,则光线所照区域最大范围 B P 为 cm .
三、解答题(本题有5小题,共46分,解答应写出文字说明、证明过程或演算步骤)
-
19. 如图是由边长为1的小正方形组成的6×6网格,每个小正方形的顶点叫做格点,线段AB的两个端点都在格点上,仅用无刻度的直尺在给定网格中完成画图.
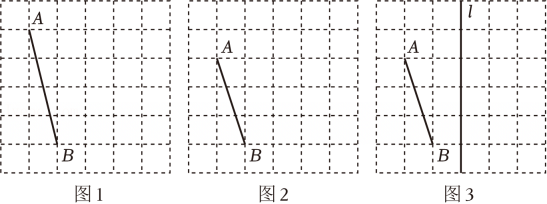 (1)、在图1中以线段AB为边作锐角△ABC(点C在格点上),使其成为轴对称图形(作出一个即可);(2)、在图2中以线段AB为腰作等腰直角△ABC(作出一个即可),△ABC的面积为 ▲ ;(3)、在图3中的直线l上画出点P , 使得PA+PB最短.20. 第五代移动通信技术(简称5G)是最新一代蜂窝移动通信技术,是4G、3G和2G系统后的延伸.5G的性能目标是高数据速率、减少延迟、节省能源、降低成本、提高系统容量和大规模设备连接.县电信部门要修建一座5G信号发射塔,要求发射塔离村庄A、B的距离必须相等,且到两条高速公路MN、PQ的距离也必须相等.发射塔点G应修建在什么位置?在图上标出它的位置.(请保留作图痕迹,并标注出点G,否则扣分.)
(1)、在图1中以线段AB为边作锐角△ABC(点C在格点上),使其成为轴对称图形(作出一个即可);(2)、在图2中以线段AB为腰作等腰直角△ABC(作出一个即可),△ABC的面积为 ▲ ;(3)、在图3中的直线l上画出点P , 使得PA+PB最短.20. 第五代移动通信技术(简称5G)是最新一代蜂窝移动通信技术,是4G、3G和2G系统后的延伸.5G的性能目标是高数据速率、减少延迟、节省能源、降低成本、提高系统容量和大规模设备连接.县电信部门要修建一座5G信号发射塔,要求发射塔离村庄A、B的距离必须相等,且到两条高速公路MN、PQ的距离也必须相等.发射塔点G应修建在什么位置?在图上标出它的位置.(请保留作图痕迹,并标注出点G,否则扣分.) 21. 如图, 已知 , 点 A, E, B, D 在同一直线上, A C 与 F D 相交于点 , 求证: . 请补全证明过程, 并在括号里写上理由.
21. 如图, 已知 , 点 A, E, B, D 在同一直线上, A C 与 F D 相交于点 , 求证: . 请补全证明过程, 并在括号里写上理由.
证明: ,
∴∠FED= ▲ =90°
∵AE=DB,
∵AE+ ▲ = ▲ +BD,
即AB=DE.
在Rt△ABC与Rt△DEF中,
∴Rt△ABC≌Rt△DEF( ▲ )
∴∠A= ▲
∴GA=GD( ▲ )
22. 如图,点D,E分别在△ABC的边AB,AC上,点F在线段BE上,且∠EDF=∠C,DE//BC.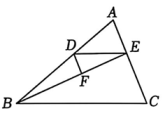 (1)、判断DF与AC的位置关系,并说明理由;(2)、若DF平分∠BDE,∠ADE=38°,求∠AED.23. 受全球气候变暖影响,今年深圳的雨水特别多.据悉,不止深圳,整个华南地区暴雨形成“列车效应”.雨水增多导致雨伞的需求量大大增加.下图是某型号雨伞的结构图.
(1)、判断DF与AC的位置关系,并说明理由;(2)、若DF平分∠BDE,∠ADE=38°,求∠AED.23. 受全球气候变暖影响,今年深圳的雨水特别多.据悉,不止深圳,整个华南地区暴雨形成“列车效应”.雨水增多导致雨伞的需求量大大增加.下图是某型号雨伞的结构图.
根据以下素材,探索完成任务,
探究雨伞中的数学问题
素材1
图1是这个雨伞的示意图.不管是张开还是收拢,是伞柄,伞骨且 , , D点为伞圈.伞完全张开时 , 如图1所示.

素材2
伞圈D能沿着伞柄滑动,如图2是完全收拢时伞骨的示意图,此时伞圈D滑动到的位置,且三点共线.测得(参考值:).

素材3
同学们经过研究发现:雨往往是斜打的,且都是平行的.如图3,某一天,雨线与地面夹角为 , 小田站在伞圈D点的正下方点G处,记为 , 此时发现身上被雨淋湿,测得 .

问题解决
任务1
判断AP位置
求证:是的角平分线.
任务2
探究伞圈移动距离
当伞从完全张开到完全收拢,求伞圈D移动的距离(精确到).
任务3
拟定撑伞方案
求伞至少向下移动距离 ▲ , 使得人站在G处身上不被雨淋湿,(直接写出答案)
24. 在△ABC中,AB=BC=2,∠ABC=90°,BP是AC边上的高线,将一块三角板的直角顶点放在点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AB、BC于D、E两点.图1和图2是旋转三角板得到的图形中的两种情况. (1)、求证:BP=CP;(2)、猜想线段PD与PE之间的数量关系,并结合图1证明你的结论;(3)、在三角板绕点P旋转的整个过程中,当△PEC为等腰三角形时,求BE的长.
(1)、求证:BP=CP;(2)、猜想线段PD与PE之间的数量关系,并结合图1证明你的结论;(3)、在三角板绕点P旋转的整个过程中,当△PEC为等腰三角形时,求BE的长.