相关试卷

1、小明同学在学习完有理数的运算后，对运算产生了浓厚的兴趣，她借助有理数的运算，定义了一种新运算“ $\oplus$ ”，运算规则为： $a \oplus b = a \times b + 2$ ．如： $2 \oplus 6 = 2 \times 6 + 2$

(1)、求 $2 \oplus 4$ 的值；

(2)、求 $(- 3) \oplus (2 \oplus \frac{1}{2})$ 的值．

查看解析
2、已知 $a 、 b$ 互为相反数， $x 、 y$ 互为倒数， $m$ 是最大的负整数，求 $6 (a + b) + |m| - 3 x y$ 的值．

查看解析
3、在数轴上表示下列各数，并用“<”把这些数连接起来．
$- 3$ ；3.5； $- (- 2 \frac{1}{2})$ ； $|- 1|$ ．

查看解析
4、计算：

(1)、 $6 + (- 4) - 2 + 3$

(2)、 $(\frac{1}{2} - \frac{2}{3} + \frac{5}{6}) \times (- 24)$

查看解析
5、如果电梯上升5米，记作+5米，那么下降8米可记作米．

查看解析
6、根据流程图中的运算程序，当输入数据 $x = - 1$ 时，输出结果 $y$ 为（）

A、9 B、 $- 9$ C、25 D、 $- 25$

查看解析
7、如图，将刻度尺放在数轴上，让 $3 cm$ 和 $5 cm$ 刻度线分别与数轴上表示2和4的两点重合对齐，则数轴上与 $0 cm$ 刻度线对齐的点表示的数为（）

A、 $- 1$ B、0 C、1 D、2

查看解析
8、一个两位数，十位上的数字是 $b$ ，个位上的数字是 $a$ ，这个两位数是（）

A、 $a + b$ B、 $10 (a + b)$ C、 $10 a + b$ D、 $10 b + a$

查看解析
9、在 $3.14$ ， 2024， $- \frac{22}{7}$ ， $π$ 四个数中有理数的个数是（）

A、1个 B、2个 C、3个 D、4个

查看解析
10、南岸区是一个充满生机和活力的市区，它古老而又年轻，区域内人口约为1200000人．则1200000用科学记数法可表示为（　　）

A、 $120 \times 10^{4}$ B、 $12 \times 10^{5}$ C、 $1.2 \times 10^{6}$ D、 $0.12 \times 10^{7}$

查看解析

11、某出租车公司推出

A

专车和

B

快车两种出租车，它们的收费方式如下：

$A$ 专车： $3$ 千米以内收费 $10$ 元，超过 $3$ 千米的部分每千米收费 $2.5$ 元，不收其他费用；

$B$ 快车：

计费项目	起步价	里程费	远途费
计费价格	$8$ 元	2元/千米	1元/千米
注：车费由起步价、里程费、远途费三部分组成，其中起步价包含里程 $2$ 千米；里程大于 $2$ 千米的部分按计价标准收取里程费；远途费的收取方式为：行车不超过12千米，不收远途费，超过 $12$ 千米的，超出的部分每千米加收 $1$ 元．

(1)、如果乘车路程是

8

千米，使用

A

专车、

B

快车出行各需支付费用多少元？

(2)、如果乘车路程是

x (x > 12)

千米，使用

A

专车、

B

快车出行各需支付的费用多少元（用含

x

的式子表示）？

(3)、如果乘车路程是

y

千米时，使用

B

快车出行的费用比使用

A

专车出行省4元，求

y

的值．

查看解析

12、定义：对于一个两位数 $x$ ，如果 $x$ 满足个位数字与十位数字互不相同，且都不为零，那么称这个两位数为“相异数”，将一个“相异数”的个位数字与十位数字对调后得到一个新的两位数，将这个新两位数与原两位数求和，同除以11所得的商记为 $S (x)$ ．例如， $a = 15$ ，对调个位数字与十位数字得到的新两位数51，新两位数与原两位数的和为 $15 + 51 = 66$ ，和66除以11的商为 $66 \div 11 = 6$ ，所以 $S (15) = 6$ ．

(1)、计算： $S (72) =$ ____；

(2)、若一个“相异数” $y$ 的十位数字是 $k$ ，个位数字是 $3 (k - 2)$ ，且 $S (y) = 10$ ，求相异数 $y$ ；

(3)、小慧同学发现若 $S (x) = 7$ ，则“相异数” $x$ 的个位数字与十位数字之和一定为7，请判断小慧的发现是否正确？如果正确，说明理由；如果不正确，举出反例．

查看解析
13、手工制作课上，劳动课吴老师组织七年级（2）班的学生用硬纸制作圆柱形茶叶筒．七年级（2）班共有48人，其中男生人数比女生人数少2人，并且每名学生每小时剪筒身55个或剪筒底130个．

(1)、七年级（2）班有男生、女生各多少人？

(2)、七年级（2）班全体同学积极参与制作圆柱形茶叶筒，要求用一个筒身配两个筒底，为了使每小时剪出的筒身与筒底刚好配套，应该分配多少名学生剪筒身，多少名学生剪筒底？

查看解析
14、小明连续记录了他家私家车 $7$ 天中每天行驶的路程（如表），以 $50 km$ 为标准，多于 $50 km$ 的记为“ $+$ ”，不足 $50 km$ 的记为“ $-$ ”

第一天
第二天
第三天
第四天
第五天
第六天
第七天
路程 $(km)$
$- 8$
$- 10$
$- 14$
$10$
$- 16$
$+ 31$
$+ 7$

(1)、在这七天中，最远与最近路程差是多少千米？

(2)、若行驶 $1 km$ 需用汽油 $0.08$ 升，汽油价格为 $8$ 元 $/$ 升，请计算小明家这 $7$ 天的汽油费用是多少元？

查看解析
15、如图所示的图形由一个正方形和一个长方形组成．

(1)、求该图形的面积（用含 $x$ 的式子表示）；

(2)、若 $x = 1$ ，求该图形的面积．

查看解析
16、画一条数轴，并把 $- 3$ ， $1$ ， $- 1 \frac{1}{2}$ ， $3$ 表示在数轴上，并用“ $<$ ”连接起来．

查看解析
17、先化简，再求值： $2 (x^{2} y + x y) - (x^{2} y - 2 x y) - 8 x y$ ，其中 $x = 2$ ， $y = \frac{1}{4}$ ．

查看解析
18、（1）计算： $|- 5| + (- 4) - (- 9)$
（2）解方程： $5 (x - 1) + 2 = 3 - x$

查看解析
19、如图，已知数轴上点 $A$ 表示的数为 $a$ ，点 $B$ 表示的数为 $b$ ，满足 $|a - 6| + {(b + 4)}^{2} = 0$ ．动点 $P$ 从点 $A$ 出发，以每秒6个单位长度的速度沿数轴向左匀速运动，动点 $Q$ 从点 $B$ 出发，以每秒3个单位长度的速度沿数轴向左匀速运动，设运动时间为 $t (t > 1)$ 秒．若点 $P$ ， $Q$ 同时出发，点 $P$ 与点 $Q$ 之间的距离为4个单位长度时， $t =$ ．

查看解析
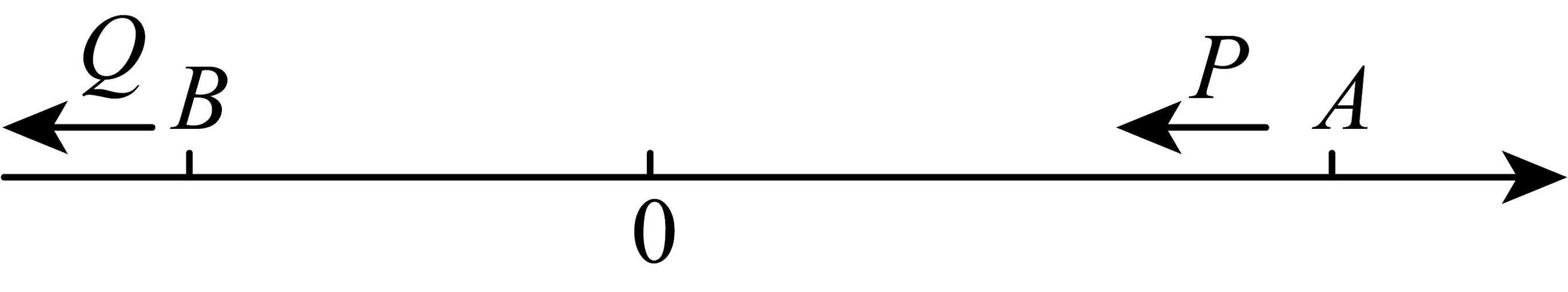
20、计算机的二进制数据是用 $0$ 和 $1$ 两个数码来表示的数，进位规则是“逢二进一”，二进制数和十进制数可以互换，例如，二进制“ $011011$ ”转换成十进制数表示的数为 $0 \times 2^{5} + 1 \times 2^{4} + 1 \times 2^{3} + 0 \times 2^{2} + 1 \times 2^{1} + 1 \times 2^{0} = 27$ ．依此算法，二进制“ $01011$ ”转换成十进制数表示的数是．

查看解析

上一页 311 312 313 314 315 下一页跳转

	第一天	第二天	第三天	第四天	第五天	第六天	第七天
路程 $(km)$	$- 8$	$- 10$	$- 14$	$10$	$- 16$	$+ 31$	$+ 7$